分布式空间复用的实现方法与应用

在具有多个源、中继和目的节点的网络中，可实现所有的源节点向目的节点传送多个数据流而不相互干扰的传输方案叫做分布式空间复用。

分布式空间复用传输场景下，当多个源节点发送多个独立的数据流时，这些数据流在中继节点和目的节点处将会互相干扰，因而分布式空间复用传输的主要困难是对系统进行适当的设计以使得目的节点接收到没有干扰的信号。为此，我们可以通过对源节点、中继节点和目的节点三处或其三处中的任意组合实施干扰消除技术来消除数据流间的干扰。源节点、中继节点和目的节点的处理形式的设计取决于多个因素，比如：节点间是否存在协同，或节点是否存在严格的能量限制从而要求复杂度不能过高等。源节点、中继节点和目的节点的任意组合方式下的干扰处理技术早已提出，可以参考文献[296，409-416]。

在本节中，针对两跳AF中继网络，我们讨论基于迫零策略^[416]的4种不同的系统方案。即考虑在下面4种位置采用迫零预编码和/或迫零检测技术：源节点和中继节点、中继节点、中继节点和目的节点、目的节点。迫零算法是一种实用且简单的干扰消除方案。针对上述4种系统场景，下面将分别研究其对应的中断概率^[416]。

3.3.3.1 系统模型

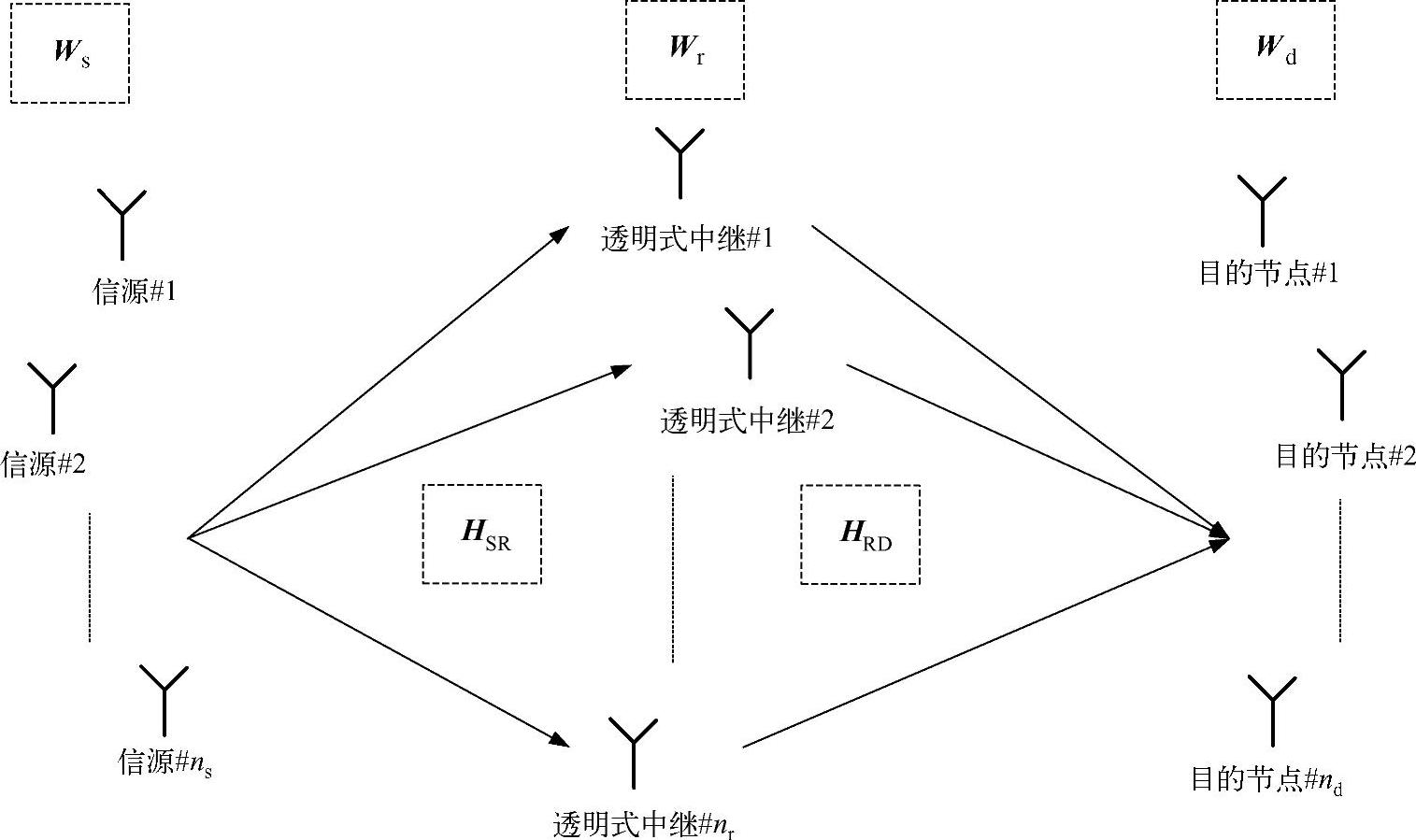
图3.15 分布式空间复用系统

考虑具有n_s个源节点，n_r个中继节点和n_d个目的节点的无线通信系统，如图3.15所示。P_s和P_r分别表示所有源节点和中继节点的发射功率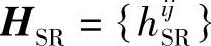；和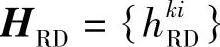分别表示n_r×n_s维的源-中继链路的信道矩阵和n_d×n_r维的中继-目的链路的信道矩阵，其中h^ij_SR表示源天线j与中继天线i之间的信道衰落值，h^ki_RD表示中继天线i与目的天线k之间的信道衰落值；W_s，W_r和W_d分别表示n_s×n_s度源节点权矩阵、n_r×n_r维中继节点权矩阵和n_d×nd维目的节点权矩阵；n_SR和n_RD分别为中继节点处和目的节点处的噪声矢量，每个噪声分量都是每维功率谱密度为N₀/2的高斯随机变量。

首先，源节点向n_r个中继节点广播信号矢量X，X由n_s个数据流组成，且满足E（X^HX）=1。中继节点处的接收信号矢量可以表示为

Y_SR=Q_sH_SRW_sX+n_SR （3.89）

其中，Q_s为归一化系数，以保证源节点处的长期总发射功率归一：

其中，

接着，中继节点用权值矩阵Q_rW_r对来自源节点的接收信息Y_SR进行加权处理并转发至目的节点。目的节点的接收信号可以表示为

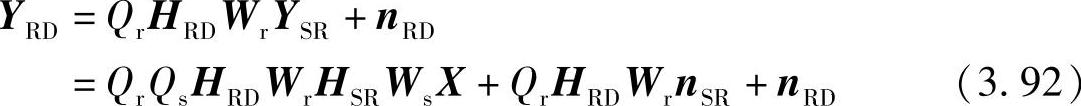
其中，Q_r为归一化系数，以保证中继节点处的长期总发射功率归一：

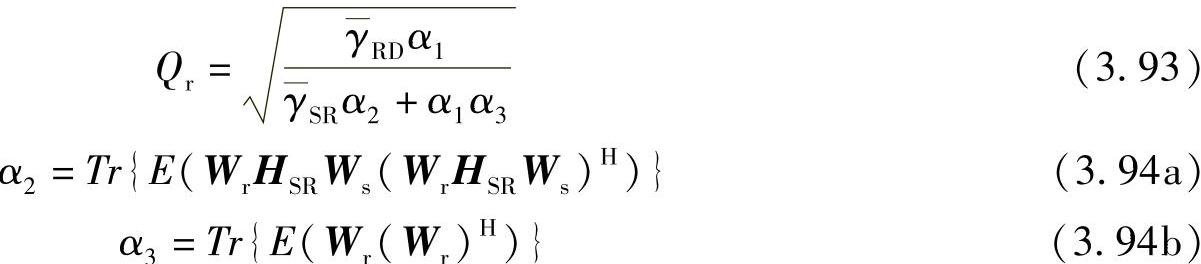
其中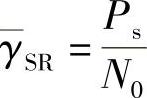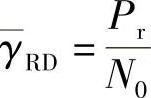，，。需要说明的是，由于短期功率限制不易处理，在此仅考虑长期功率限制。

最后，目的节点对接收信号Y_RD乘以权值矩阵W_d，得到估计信号：

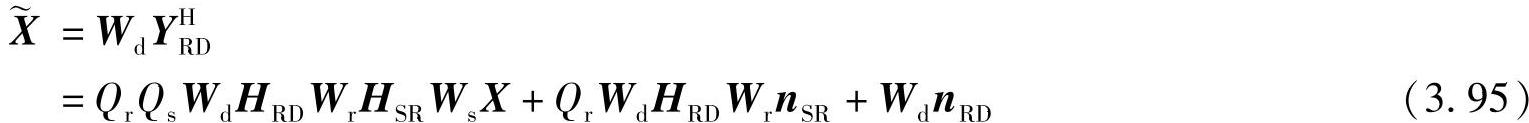
对于第k个数据流，目的节点处的接收信噪比可以表示为

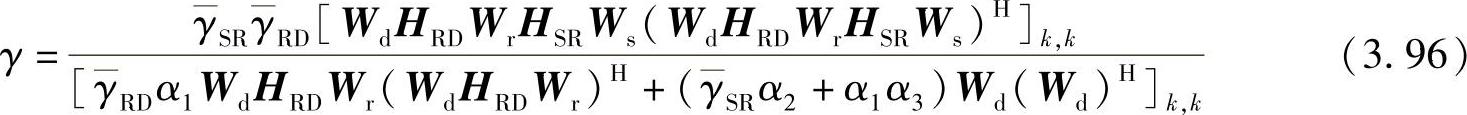
其中，[A]_k，k表示矩阵的第k行，第k列的元素。

为了使得目的节点获得的信号无干扰，我们采用迫零准则来设计权值矩阵W_s、W_r和W_d。同时，权值矩阵的设计依赖于源、中继和目的节点处的处理能力，而处理能力又取决于各节点处的协同能力、能量限制和反馈能力等。

为了便于迫零处理，我们假设存在节点间的协同通信。例如，如果在源节点和中继节点进行迫零处理，我们假定源节点之间可以协同通信，中继节点之间也可以进行协同通信。在本节中，协同通信是指需要协同的节点之间能够进行信道信息和传输的信息符号的交换，从而使得迫零处理容易实施。对于协同节点是同一个实体（比如基站）的不同天线端口的特定场景，我们的结论同样适合。由于这个场景在实际中更普遍，在接下来的章节中我们都在该场景下研究不同的方案。尽管如此，我们的结论同样适用于多个源节点、中继和目的节点的一般场景。

最后我们做一般性假设：使用迫零算法的节点数目大于或等于链路另一端的节点数目。例如：如果在源节点和中继节点进行迫零处理，则系统满足：n_s≥n_r和n_r≥n_d。

在接下来的章节中，我们将分别对文中提出的基于迫零设计策略的4种不同的系统配置进行性能研究，并引用下面的定理^[417]以获得中断概率。

定理3.3.2：令V表示n×m维的零均值、方差为I_n⊗I_m的复正态高斯变量，且m≥n，则有

3.3.3.2 在源和中继节点处进行迫零

在本节中，我们介绍在源节点和中继节点处进行迫零设计的分布式空间复用。这跟很多实用场景相对应，在这些场景中源节点之间和中继节点之间均进行协同，但是目的节点间不进行协同。一个简单的例子是，一个配置了多天线的基站通过一个多天线的基站式中继向多个目的手机发送信息，手机由于能量限制不能进行过多的信号处理。在这个例子中，源节点和中继分别对应于基站和基站式中继上的单根天线。

由于在源和中继节点处进行迫零操作，系统需满足n_s≥n_r和n_r≥n_d。根据迫零原则，可以得到W_s、W_r和W_d：

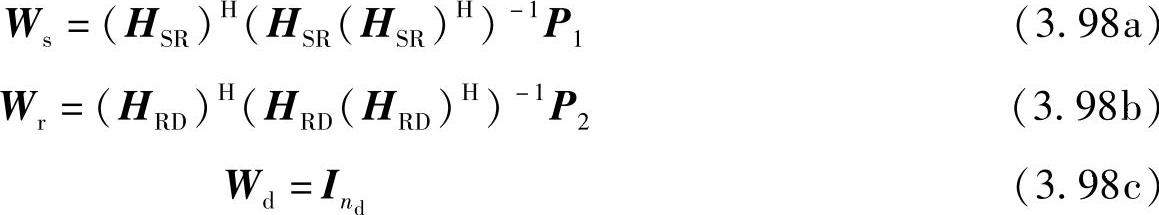
其中，P₁是源节点处从n_s个数据流中选出n_r个数据流的置换矩阵，维度为n_r×n_s；P₂是中继节点处从n_r个数据流中选出n_d个数据流的置换矩阵，维度为n_d×n_r；通过将一个n_r×n_r维置换矩阵和一个n_r×（n_s-n_r）维全零矩阵进行横向合并得到P₁，同时将一个n_d×n_d维置换阵和一个n_d×（n_r-n_d）维全零矩阵进行横向合并得到P₂。下面举例进行说明，假设n_s=4，n_r=3和n_d=2，P₁和P₂的一种可能取值如下：

置换矩阵的选择可以实现对某些数据流进行优先排序，或者为每个数据流分配相等的时间周期。对于第一种情况，可以通过根据各自的信道状态信息，选用性能最好的数据流来实现。对于第二种情况，可以通过采用循环方式选择置换矩阵来实现。这里我们本着公平原则来选择置换矩阵，因而对任何信道状态信息都随机地选择置换矩阵。

将式（3.98）代入式（3.96），第k个数据流的信干噪比（SINR）接近于一个常数：

其中，

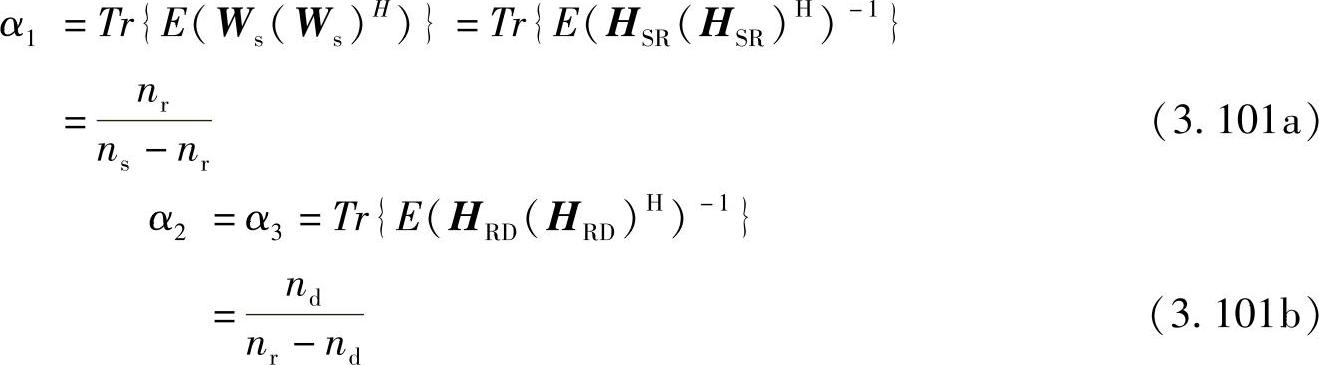
根据式（3.101a）和式（3.101b），可将式（3.90）和式（3.93）等效为：

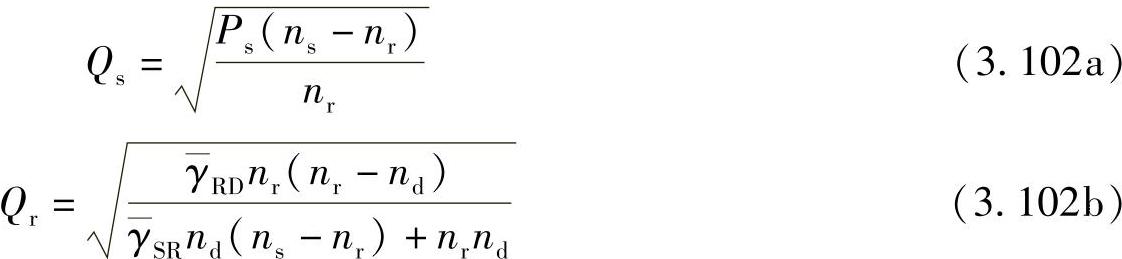
进而，式（3.100）所示的SINR可以进一步等效为：

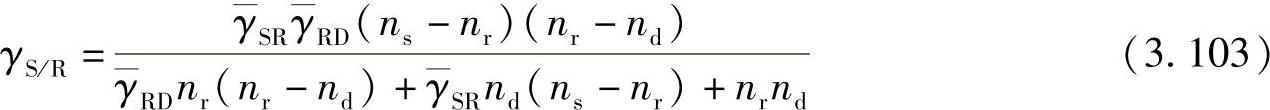
考虑γ_S/R与n_s的关系，容易发现SINR是n_s的增函数。并且，从式（3.102a）和（3.102b）可知，随着n_s的增加，源节点处的归一化系数随之增加，进而降低了中继节点处的SINR。但是，由式（3.102b）可知，随着n_s的增加，中继处的归一化参数却随之降低。以上表明，相对于由n_s增加带来的源节点处归一化系数的有利影响，中继处归一化系数的不利影响占据主导地位。

进一步考虑γ_S/R与n_d的关系，很容易可知SINR是n_d的增函数。这是由于，随着目的节点的接收天线数量的增加，中继处的归一化常数会随之变小，进而提高接收SINR。

同理，考虑γ_S/R与n_r的关系，很容易可知SINR是n_d的增函数。由于表达式比较复杂，不能直接得到有用结论。因此，考虑当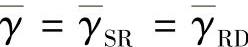时，当且仅当式（3.104）满足时，SINR是n_r的增函数。

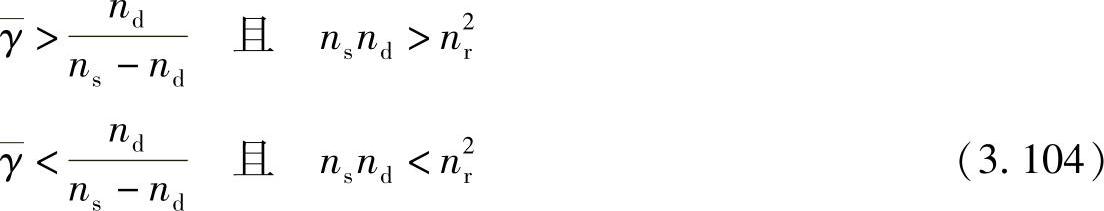
观察式（3.104）可得，只有满足一定的功率和天线限制，SINR才是n_r的增函数。同时，增加中继数具有双重作用：降低源节点处的归一化系数和增加中继节点处的归一化系数。式（3.104）中的条件正好反映了发挥这两种作用的界限。这在设计中继数目时非常有用，可达到增加SINR的目的。

图3.16给出了源节点和目的节点数目固定时，不同中继数对应的SINR曲线。通过式（3.100）得到的“解析”曲线跟蒙特卡洛仿真曲线非常一致。观察图3.16可以发现，当中继节点数目从3增加到4时，SINR随之增加。但是，随着中继数目的进一步增加，SINR开始降低。这跟我们之前的分析一致：中继节点数目的增加具有双重作用，即降低源节点处的归一化系数和增加中继节点处的归一化系数。同时，从图3.16还可以得出：当中继数目较少时，降低源节点处归一化系数带来的积极影响占主导地位，但是随着中继数目进一步增加，增加中继节点处归一化系数带来的消极影响占主导地位。

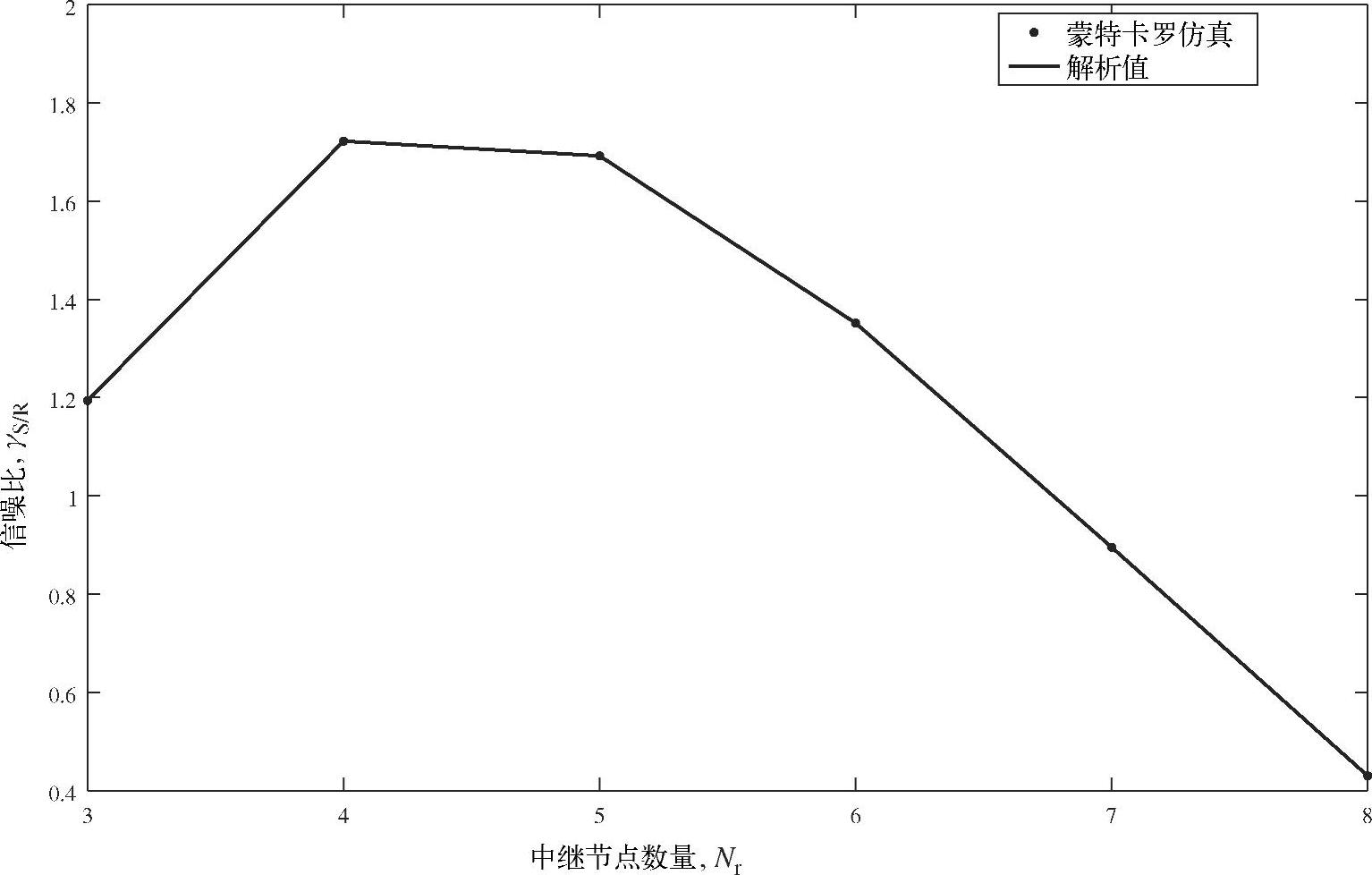
图3.16 n_d=2、n_s=9和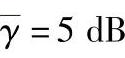时不同中继节点数对应的SINR取值曲线

3.3.3.3 在中继节点处进行迫零

在本节中，我们研究中继节点处进行迫零设计的分布式空间复用。这跟很多实用的场景对应，在这些场景中仅中继节点间进行协同通信，但是源节点间和目的节点间均不进行协同通信。一个简单的例子是，多个手机节点通过一个多天线的基站式中继向多个目的手机传输信息，由于能量限制，手机节点不能进行过多的操作。在这个例子中，中继节点与基站式中继上的单个天线相对应。我们考虑在中继节点处进行迫零预编码和迫零检测。由于仅在中继节点处进行迫零操作，需满足：n_r≥n_s、n_r≥n_d，这样，端到端的数据流数目或者端到端的空间复用增益为min（n_s；n_d）。由于受数学问题可解性的限制，只有满足n_r≥n_d且N=n_s=n_d时，我们的结论才有效。根据迫零原则，可以得到W_s、W_r和W_d：

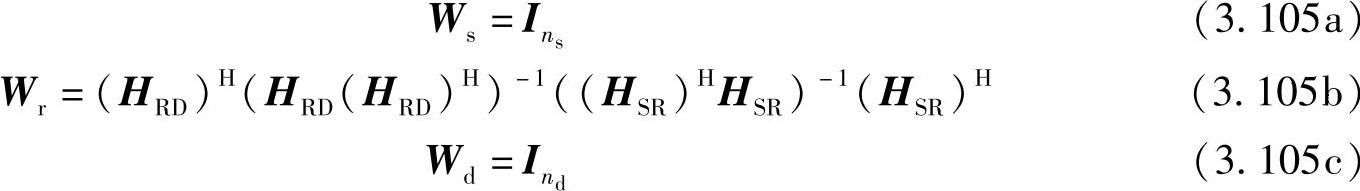
将式（3.105）代入式（3.96），第k个数据流的SINR可以等效为

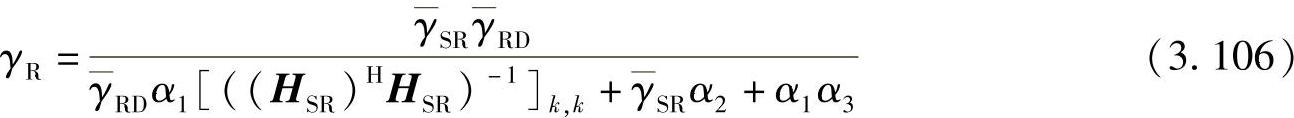
其中，

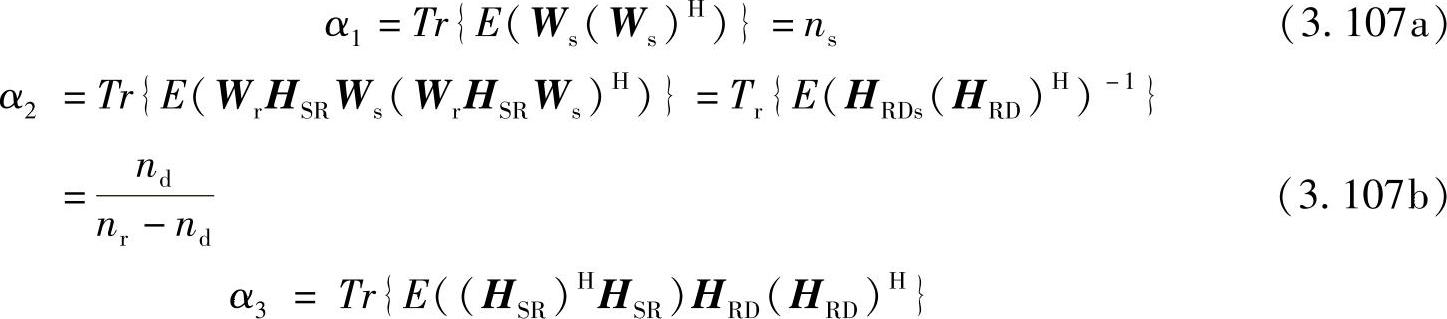
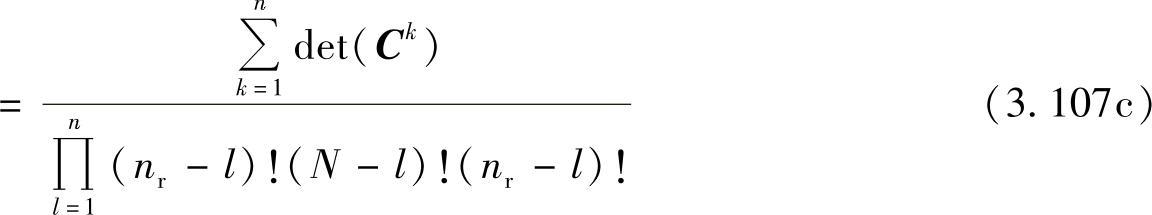
其中，C^k是一个N×N的矩阵，第ij个元素满足

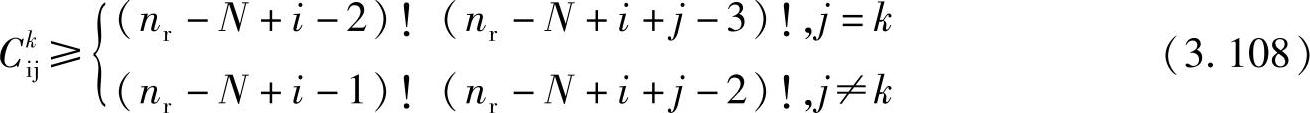
将这些结果代入式（3.90）和式（3.93）：

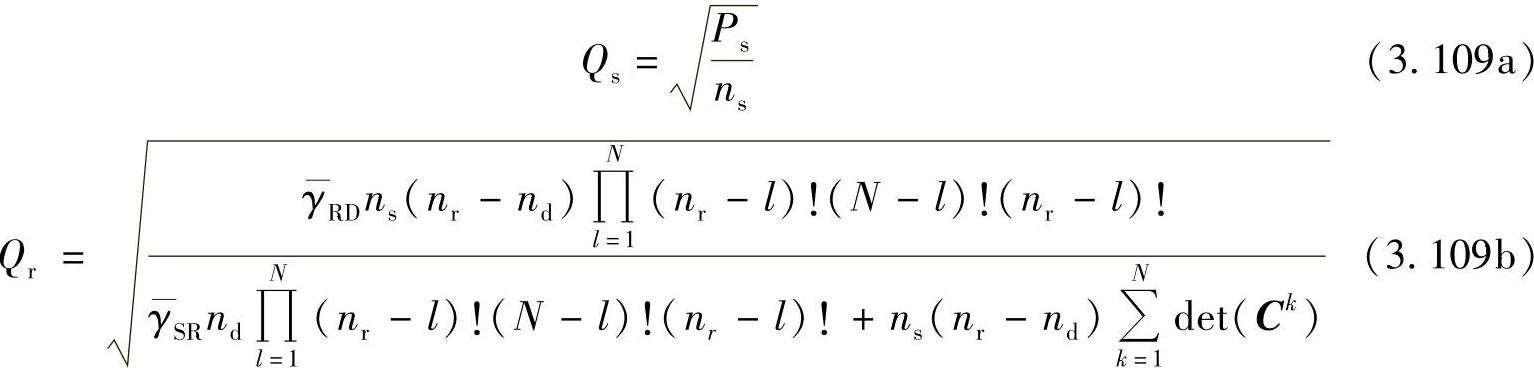
SNR很高时，Q_r可进一步简化为(www.xing528.com)

通过以上的这些等式，可以得到下面定理中的中断概率。

定理3.3.3：在两跳放大转发中继网络中，中继节点处进行迫零设计的中断概率为^[416]：

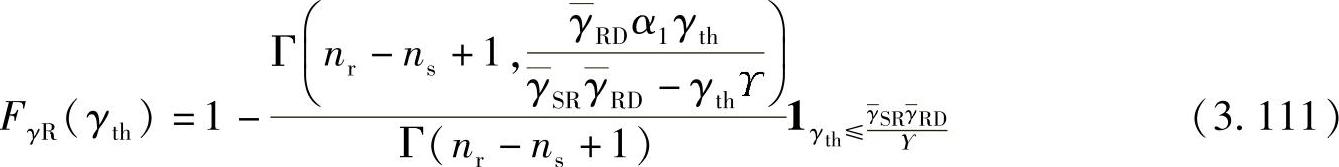
其中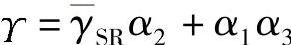，；Γ（·）是伽玛函数；Γ（·，·）是高阶不完整伽玛函数。

对式（3.111）在γ_th=0处进行泰勒级数展开，在高SNR值、高γ_SR值和高γ_RD值时，可以得到近似的中断概率^[416]：

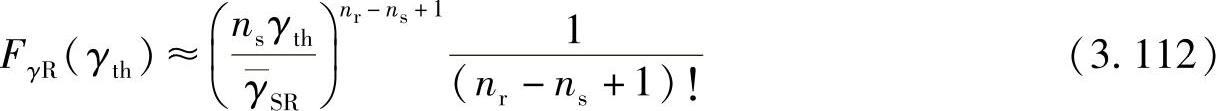
根据文献[383]可知：如果γ的CDF的一阶扩展可以表示成如下形式，

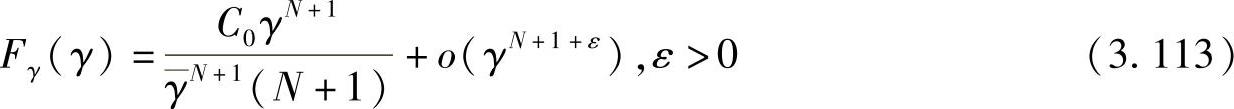
则高SNR条件下的近似中断概率表示为^[383]：

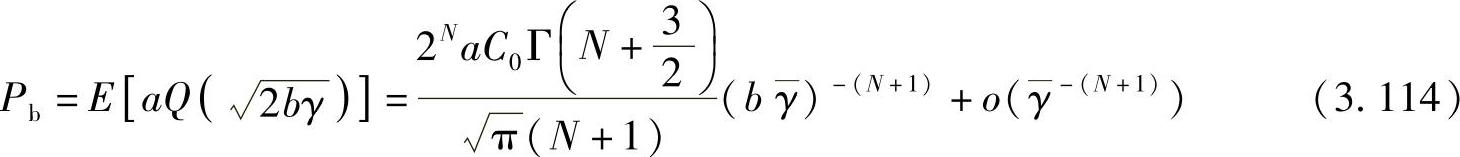
其中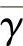，为平均传输SNR。该系统获得的分集度为N+1。由式（3.113）和（3.114），我们可以很容易得到BER的近似表达式，并且获知在中继节点进行迫零设计的分布式空间复用系统的分集度为n_r-n_s+1。式（3.112）有助于分析系统性能：近似中断概率与目的节点数目无关，并且当n_r-n_s固定时，增加n_s会引起中断概率增大，因而不利于系统的性能。

图3.17给出了源节点和目的节点数为n_s=n_d=2、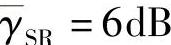和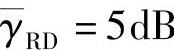时，不同中继数对应的中断概率曲线。其中由式（3.111）得到的“解析”曲线与蒙特卡洛仿真得到的曲线一致。从图3.17可以看出，中断概率随着中继节点数目的增加具有明显的下降趋势。这是因为增加中继节点数会增加源节点和中继链路的分集度，进而降低中继处的归一化系数。

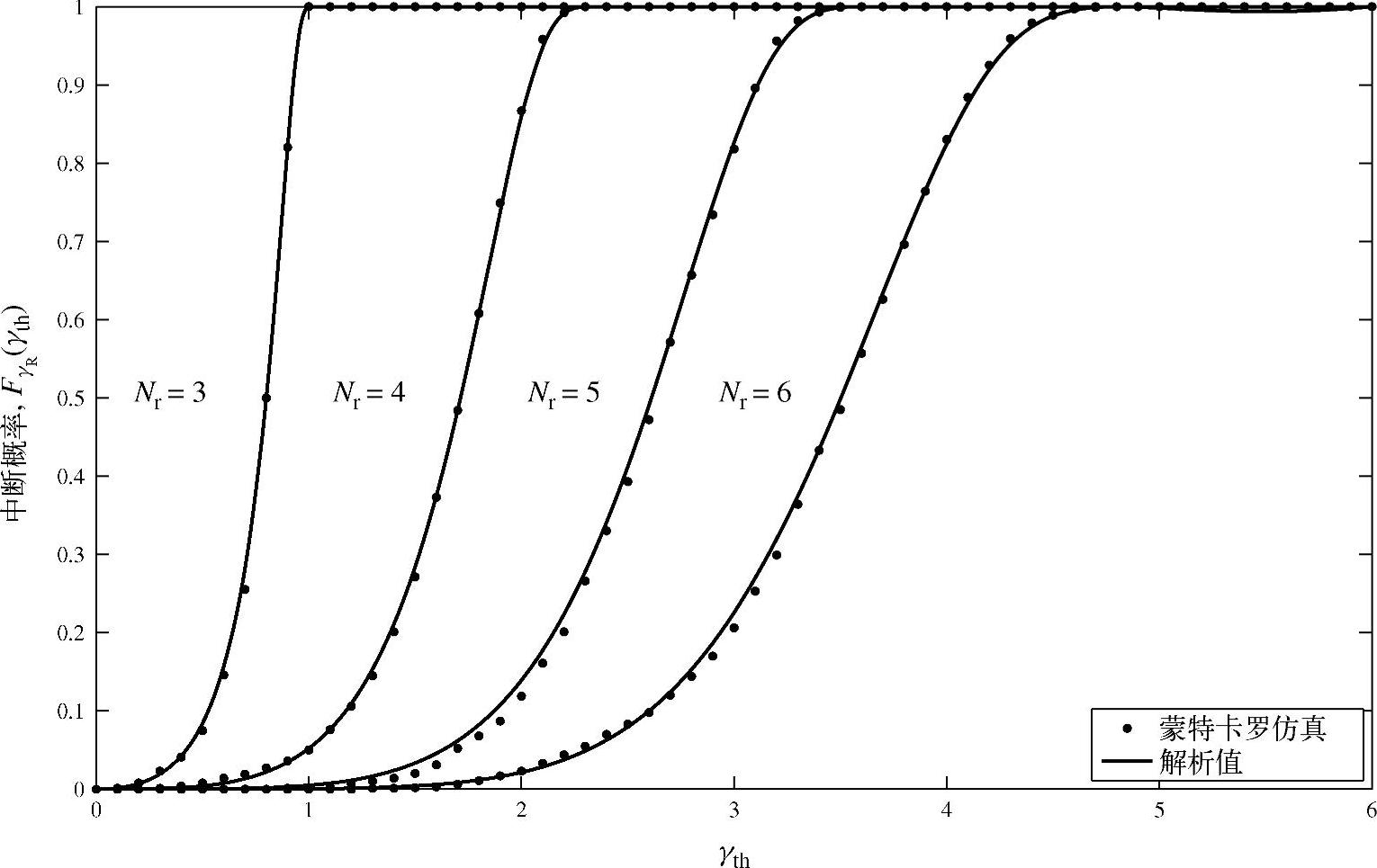
图3.17 在中继节点处进行迫零对应的中断概率曲线

3.3.3.4 在中继节点和目的节点处进行迫零

在本节中，我们研究中继节点和目的节点处进行迫零设计的分布式空间复用。这也跟很多实用的场景对应，在这些场景中，中继节点间和目的节点间均进行协同通信，但是源节点间不进行协同通信。一个简单的例子是，多个手机节点通过一个多天线的基站式中继向基站发送信息，由于能量限制，手机节点不能进行过多的操作，并且基站配置多根天线。在这个例子中，中继节点和目的节点分别与基站式中继和目的基站上的单个天线相对应。

在中继节点和目的节点处进行迫零操作，需满足n_r≥n_s且n_d≥n_r，这样，端到端的数据流数或者端到端的空间复用增益为n_s。由于受数学问题的可解性限制，只有满足n_r＞n_s时，我们的结论才有效。根据迫零原则，可以得到W_s、W_r和W_d：

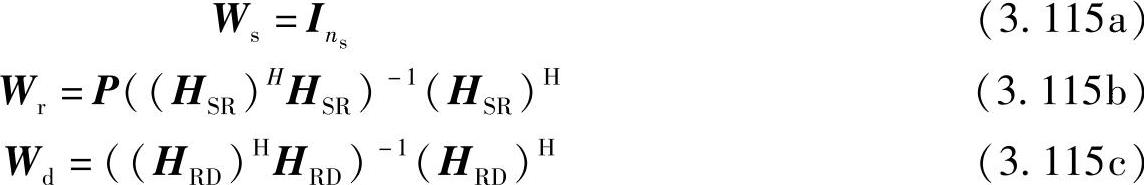
其中，P矩阵保证了中继处只有n_r个数据流被发送。在中继处采用迫零矩阵进行处理后，n_s个数据流被n_r≥n_s个中继节点发送。因而，额外的n_r-n_s中继没有被有效利用。采用诸如分集技术^[418]等先进的信号处理技术可以充分利用额外的n_r-n_s个中继，从而得到更好的BER性能。而在本节中，我们暂不考虑对中继处的传输数据流采用先进的信号处理技术。

将式（3.115）代入式（3.96），第k个数据流的SINR可以等效为

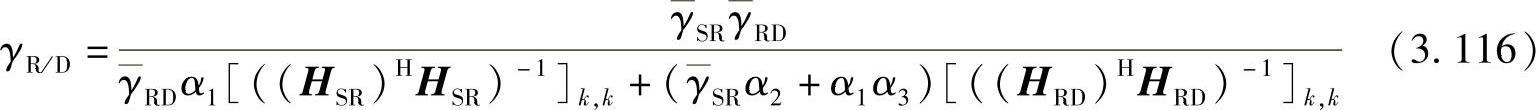
其中，

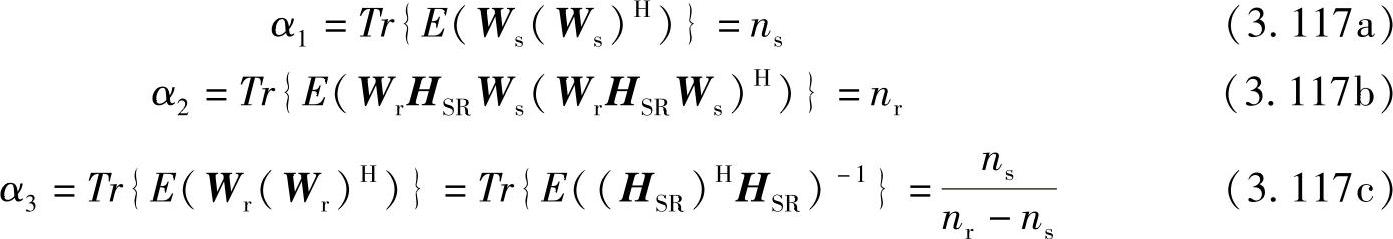
需要说明的是，上述公式仅在n_r＞n_s时才成立。

将式（3.117）代入式（3.90）和式（3.93），可以得到

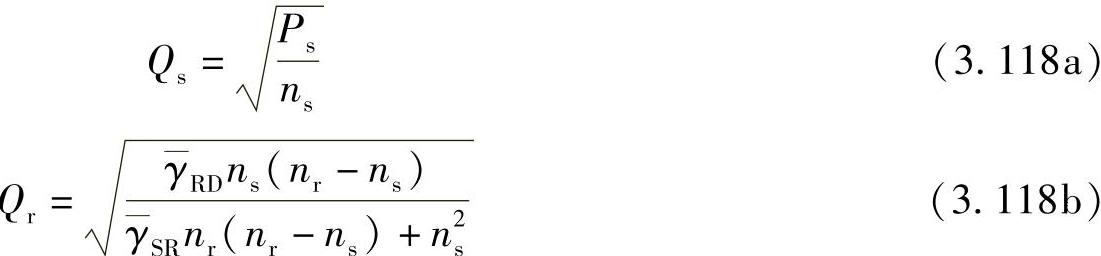
通过SINR的表达式，可得到以下定理中的中断概率。

定理3.3.4：两跳放大转发中继网络中，在中继节点和目的节点处进行迫零设计时的中断概率为^[416]：

其中，K（·）表示经过第二类修正贝塞尔函数。

高SNR时，式（3.119）可以进一步近似为^[416]：

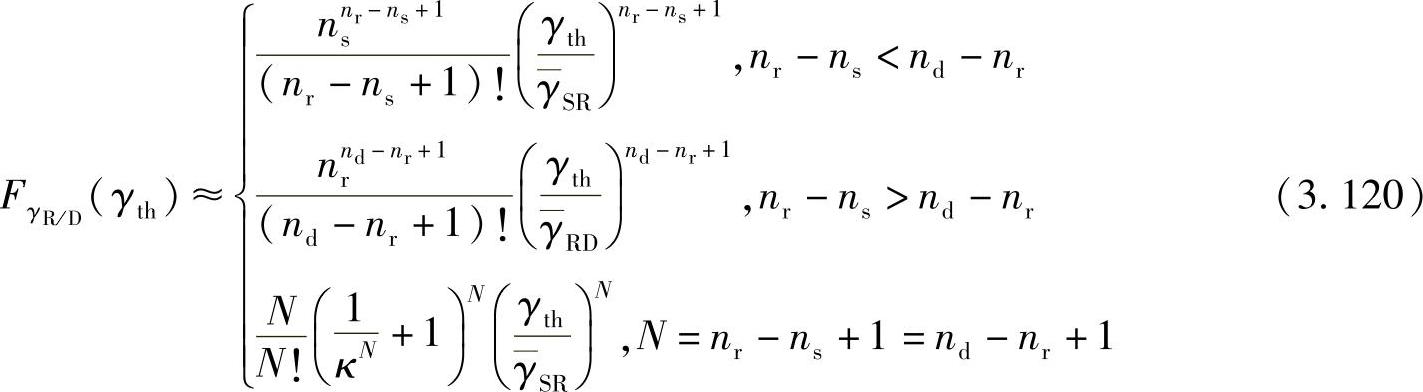
其中，。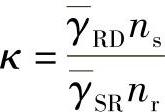

同样，基于式（3.113）和式（3.114），系统的分集度可以表示为^[416]：

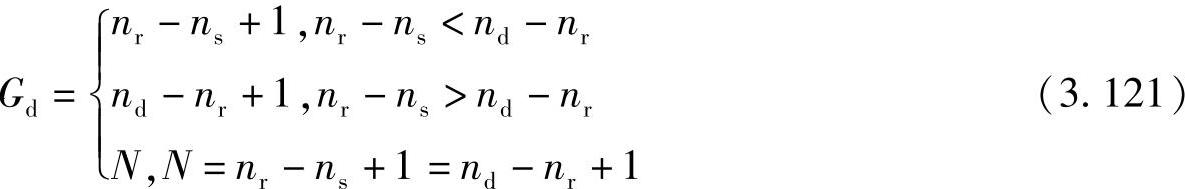
通过式（3.120）和式（3.121），我们可以得到如下结论：分集度取决于特定的源节点、中继节点和目的节点的天线参数配置。具体来说，从式（3.121）知，当n_s和n_d取值固定且n_r取值较小时，分集度n_r-n_s+1随着n_r的增加而增加，这样有利于系统性能的提高；但是随着n_r进一步增加达到某一特定值时，分集度将会变为n_d-n_r+1，此时其取值随着n_r的增加而降低，不利于系统性能的提高。同时，当n_r-n_s固定且n_r-n_s＜n_d-n_r时，随着n_s的增加，中断概率随之增加，不利于系统性能的提高；当n_d-n_r固定且n_r-n_s＞n_d-n_r时，中断概率随着n_r的增加而增加，不利于系统性能的提高。图3.18给出了源节点和中继节点数分别为n_s=2、n_r=3且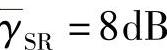和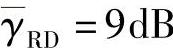时，不同目的节点数目对应的中断概率曲线。其中由式（3.119）给出的“解析”曲线与蒙特卡洛仿真得到的曲线非常一致。由于n_d的增加会提高中继-目的节点链路的分集增益进而提高系统性能，所以随着目的节点数目的增加，中断概率会大幅下降。

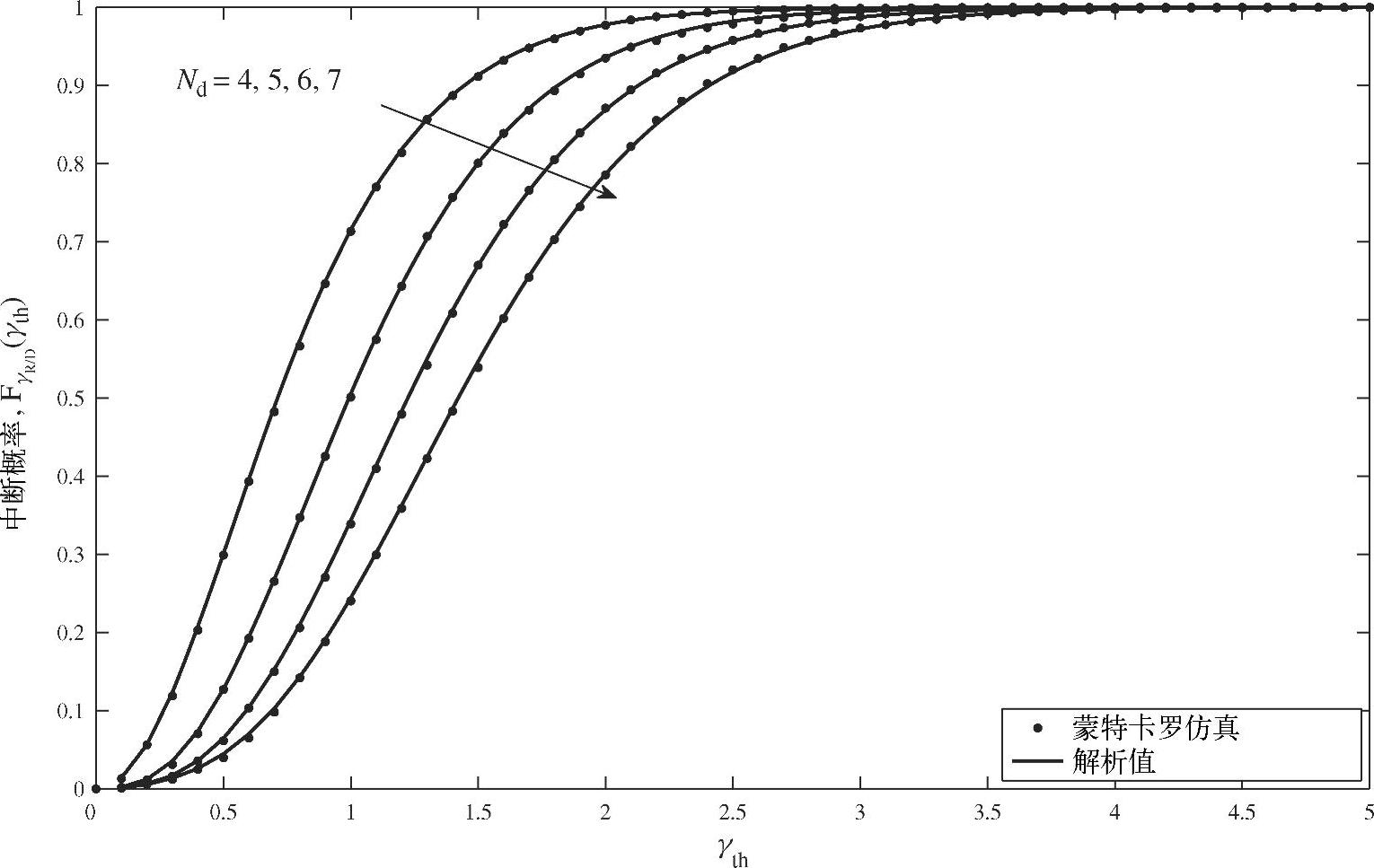
图3.18 在中继和目的节点处迫零对应的中断概率曲线

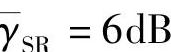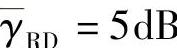图3.19给出了源节点和目的节点数分别为n_S=3、n_r=8且γ和时，不同中继节点数目对应的中断概率曲线。由图可知，当中继节点数从4增加到5时，中断概率随之降低。但是，中继节点数的进一步增加，将会引起中断概率的上升，跟之前的分析完全一致。

3.3.3.5 在目的节点处进行迫零

在本节中，我们分析目的节点处进行迫零设计的分布式空间复用方案。这跟很多实用的场景对应，这些场景中仅目的节点间进行协同通信。同时，源节点向中继节点传输独立的数据流，且中继节点向目的节点转发其接收到的数据；目的节点对其接收到的数据进行协同处理以恢复发送数据。一个简单的例子是，手机用户通过多个手机中继节点向多天线基站发送数据信息，由于能量限制，手机节点不能进行过多的操作。在这个场景中，目的节点对应于目的基站上的单个天线。

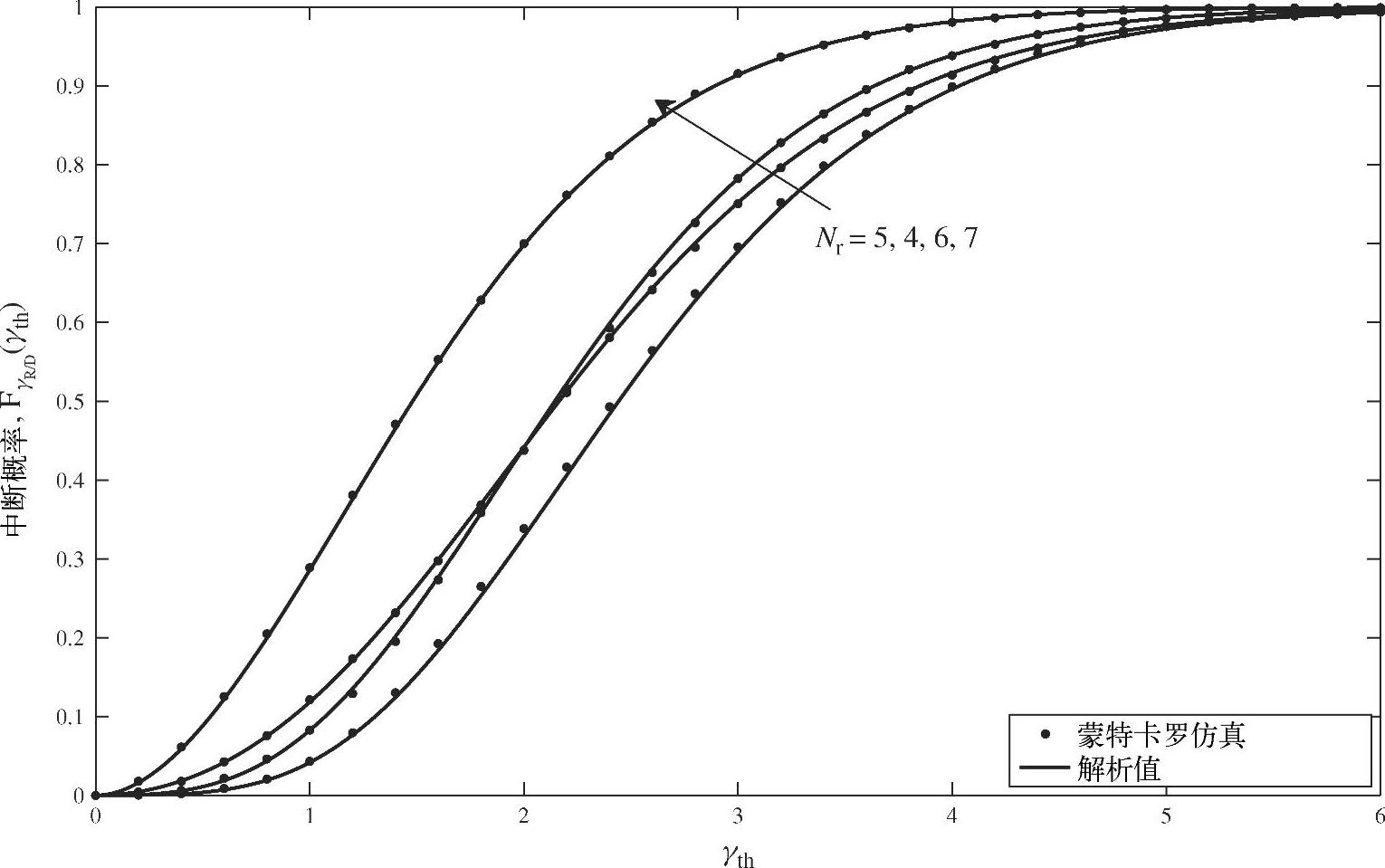
图3.19 在中继和目的节点处迫零对应的中断概率曲线

在目的节点处进行迫零操作，需满足n_d≥n_s和n_d≥n_r。这样，端到端的数据流数目或者端到端空间复用增益为min（n_s；n_r）。根据迫零原则，可以得到W_s、W_r和W_d：

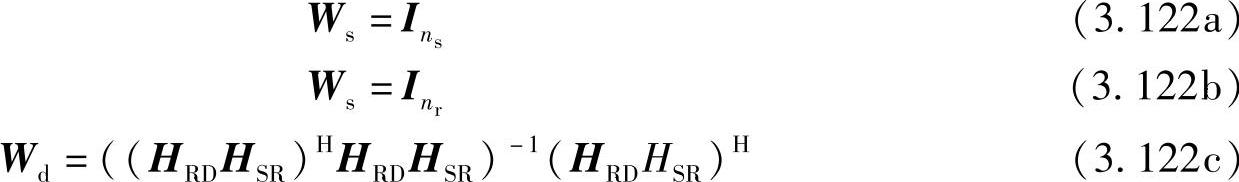
将式（3.122a）代入式（3.96），第k个数据流的SINR可以等效为

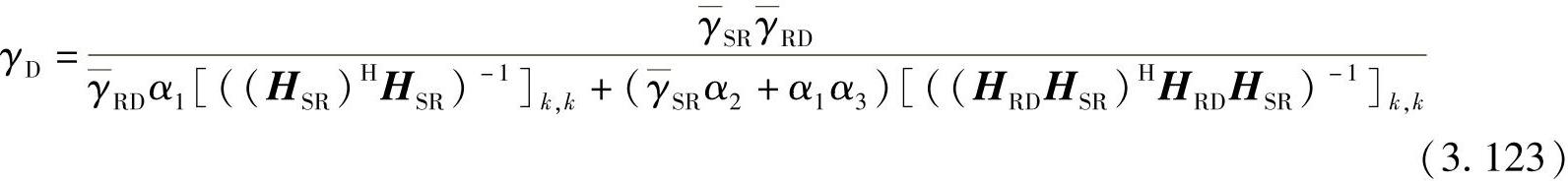
其中，

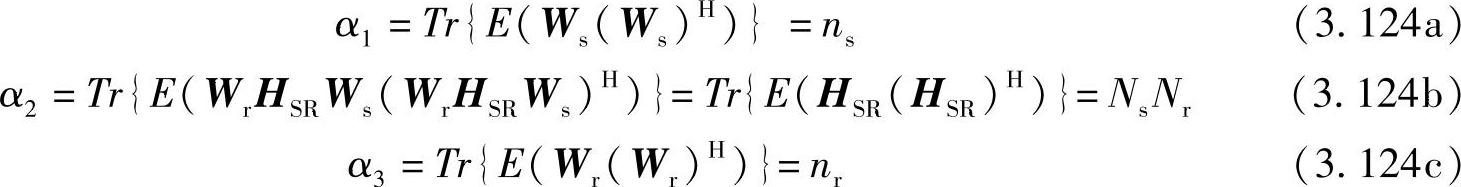
将其代入式（3.90）和式（3.93），可得

利用SINR的表达式，可得到以下定理中的中断概率：

定理3.3.5：在两跳放大转发中继网络中，目的节点处进行迫零设计时的中断概率为

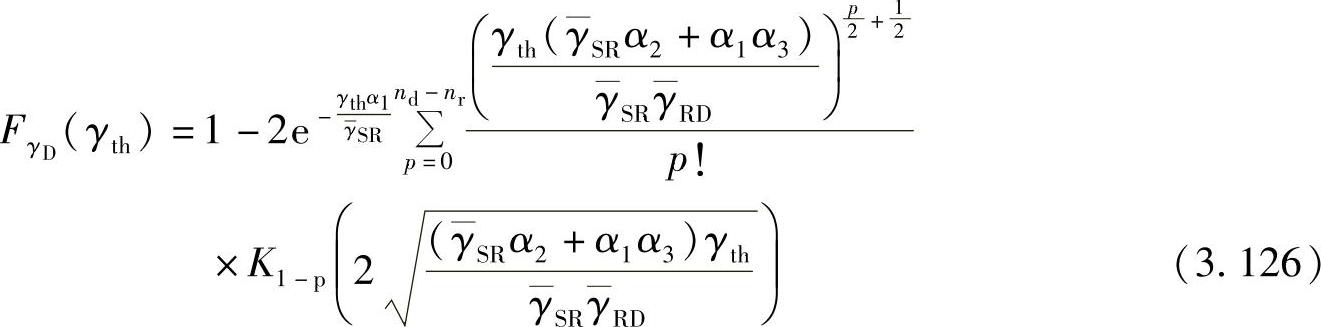
高SNR时，中断概率可以进一步近似为

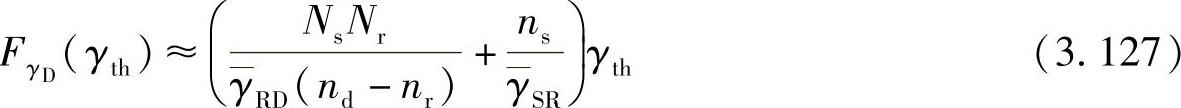
从式（3.127）可以看出，中断概率是n_s和n_r的增函数。因此，源节点和中继节点数目的增加会影响系统性能。

图3.20给出了源节点和中继节点数为n_s=n_r=2时，不同的目的节点数目对应的中断概率曲线。其中由式（3.126）给出的“解析”曲线与蒙特卡洛仿真得到的曲线非常一致。从图3.20可以看出，中断概率随着目的节点数目的增加而下降。与之前我们在高SNR得到的结论一致，同时该结论适用于所有的SNR取值。

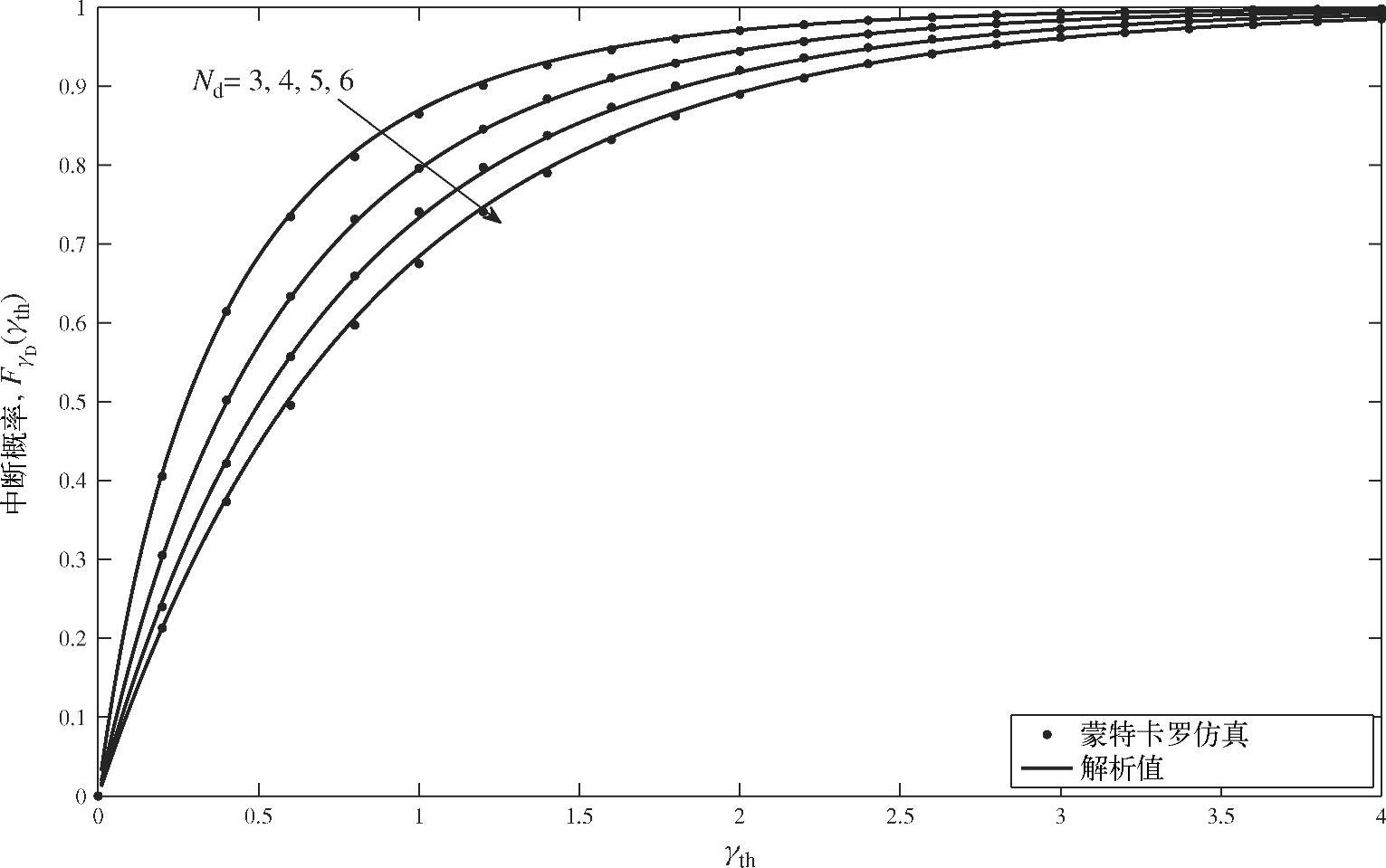
图3.20 在目的节点处进行迫零对应的中断概率-SINR曲线

图3.21给出了当源、中继和目的节点数目满足n_s=n_r=n_d-1时不同目的节点数对应的中断概率曲线。从图3.21可以发现，随着目的节点数目的增加，中断概率将快速上升。这是因为在该场景中n_r-n_d取值固定，结合式（3.127）可知，当n_r-n_d固定且信噪比高时，n_s和n_r的增加会增加系统的中断概率，从而影响系统性能。

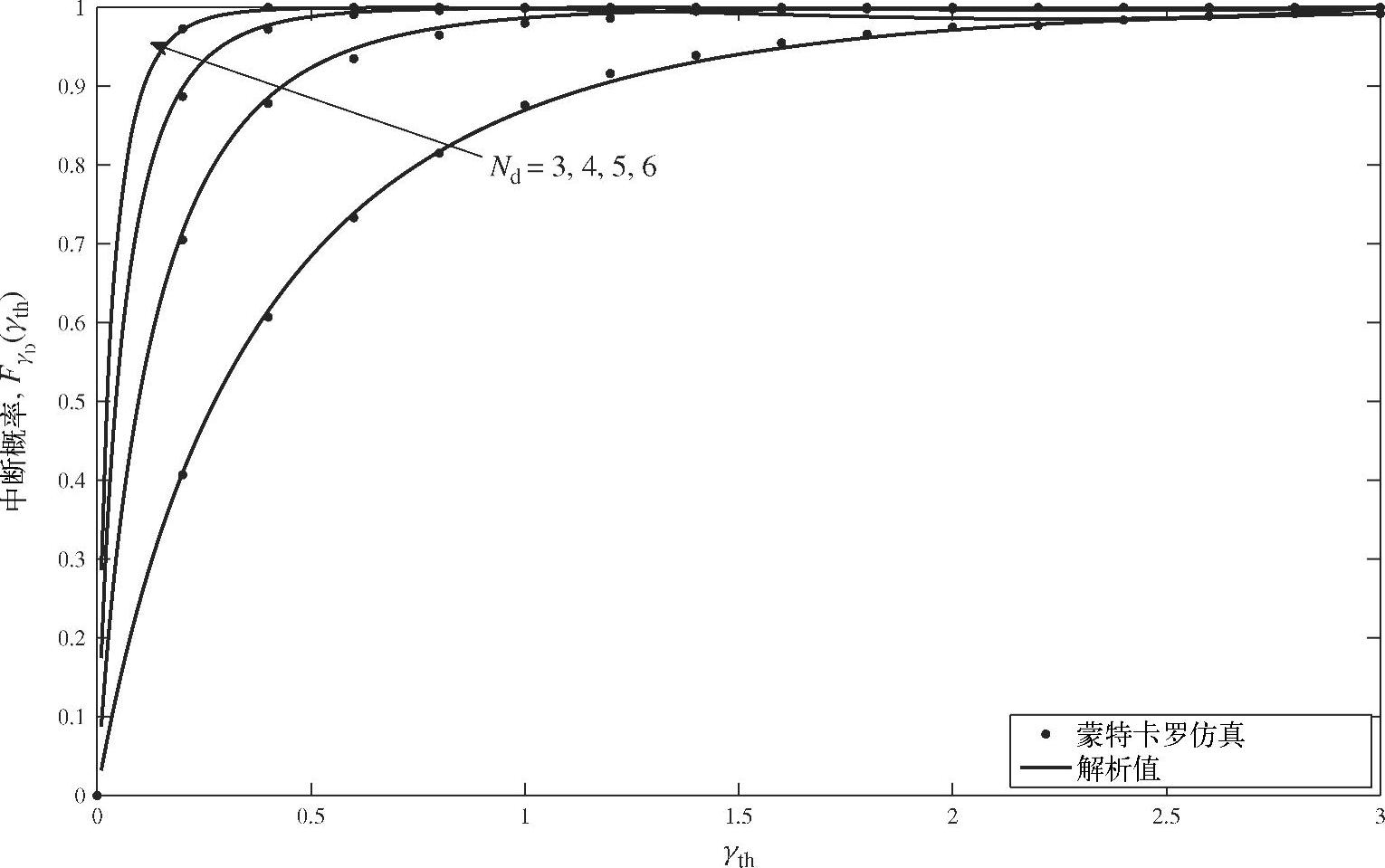
图3.21 n_s=n_r=n_d-1时目的节点处进行迫零对应的中断概率曲线