分布式空时网格码技术

尽管已有大量文献研究了再生分布式空时网格码，但针对透明传输系统的研究还很少，文献[404-407]是这方面研究的部分成果，我们将在后面讨论时引用其成果。

3.3.2.1 系统假设

考虑图3.10所示的系统的通用拓扑结构，其主要特征总结如下：

●N跳单个空时数据流的拓扑结构。

●源节点与目的节点间存在直传链路。

●采用固定的转发放大系数。

●无阴影衰落的任意平坦衰落信道。

首先假设此拓扑结构的单个数据流由N段透明转发构成，数据流中的发送符号相互干扰。因此，恰当的空时网格码处理技术就需要避免或者利用这些干扰。

Tarokh等人奠定了这一技术的基础，他们给出了慢平稳衰落信道下STTC的设计准则。在独立瑞利衰落下，平均PEP的上界为

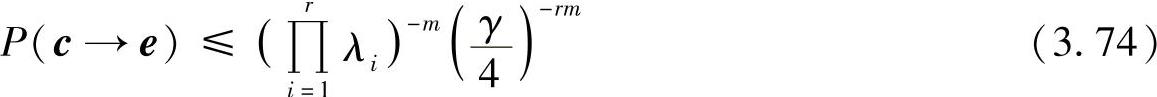
其中，c和e分别表示发送码字和错判码字；γ表示有效SNR；m和n分别表示接收天线数和发射天线数；λ_i表示码字距离矩阵A（c，e）=B（c，e）B^H（c，e）的第i个特征值，B^H为B的共轭转置矩阵，r为矩阵A的秩，其中码长为l的码字的差异矩阵B为

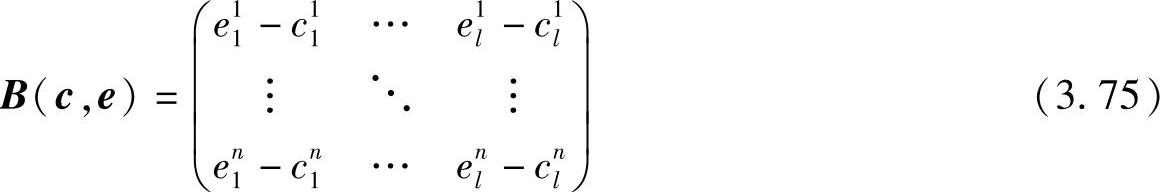
Tarokh等人的结论如下：设计的首要目标是最大化分集增益，因为它决定了错误概率曲线的斜率；因此，STTC的生成矩阵需要能生成完全满秩的码字。在生成矩阵满秩的基础上，还需最大化行列式，从而获得最大的编码增益。

Vucetic等人也推导出慢平坦衰落下STTC的设计准则，此处分集度的定义是收、发天线数目的乘积且该乘积要大于3^[408]。该分析是基于这样一个现象：随着分集度的增加，信道系数的影响逐渐消失。PEP的最终表达式为

从该上界可以看出，距离矩阵A（c，e）的迹应该最大化。

针对分布式结构框架，我们首先研究了分布式STTC结构，由分析结果可见，上述的设计准则依然适用。随后我们给出几种拓扑结构下分布式STTC的具体设计。

3.3.2.2 通用设计准则

后面的讨论均遵循Dohler在文献[404]中提出的观点。在图3.10所示的网络拓扑结构中，假设源节点有n根发射天线，目的节点有m根接收天线，并假设发送端按照Tarokh等人[122]提出的方法，在源节点的n根发射天线上对待发送的信号流进行空时格编码，随后源节点将编码数据流经由平坦衰落信道传输至中继节点，而中继节点对接收到的信号进行放大转发。目的节点的m根接收天线接收到来自中继的数据流后，按照文献[122]描述的检测算法进行检测并恢复发送数据流。

PEP的上界与等效信道的衰落系数β_i，j有关，而β_i，j是衰落系数α_i，j以及相应的放大系数A_i，j的函数，文献[122，404]中给出的PEP上界为

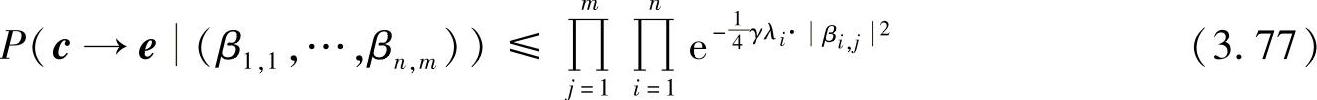
由此可得平均错误概率：

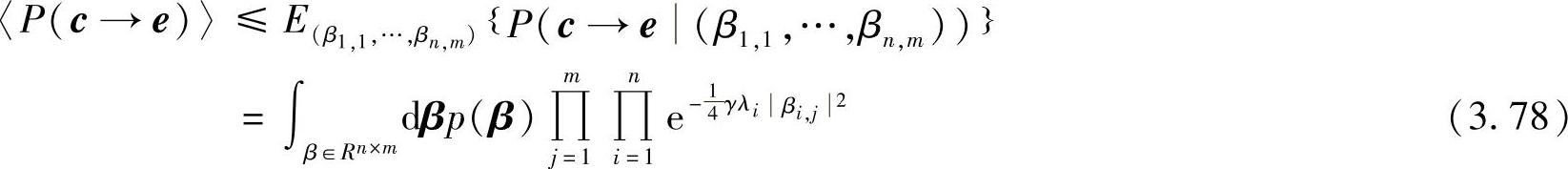
其中，p（β）是n×m维的随机矢量β=（β_1，1…β_n，m）的概率密度函数。为进一步简化上式，假设信道相互独立，则PEP上界为

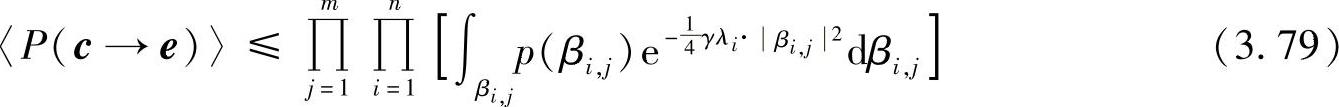
令g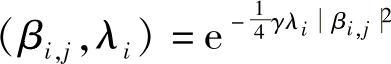，x=β_i，j，由Schwarz积分不等式可知

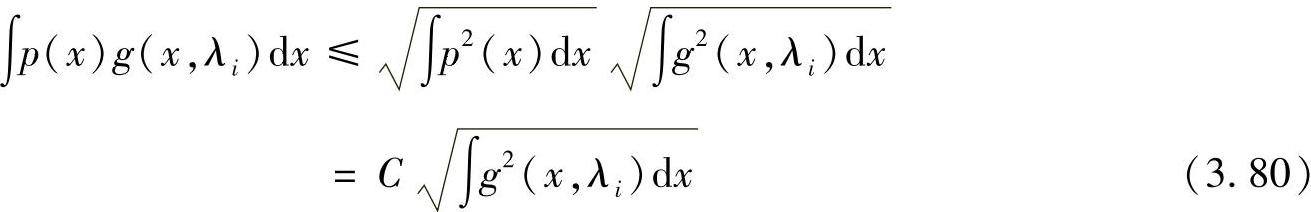
其中，p（x）可积且在定义域内其积分值有限，最终可获得PEP：

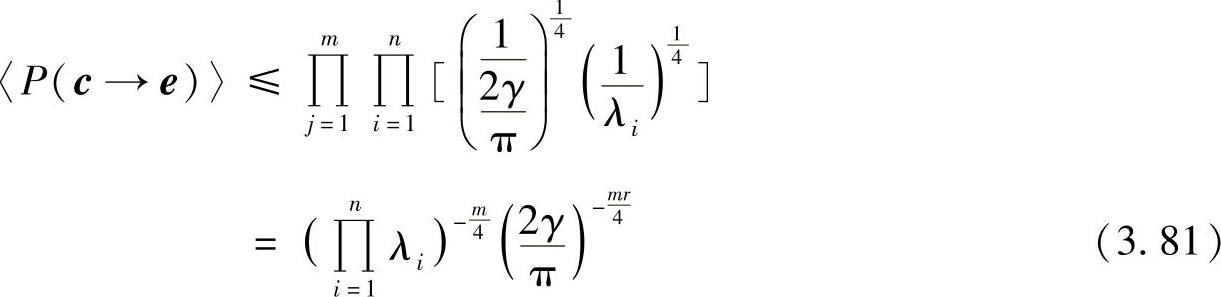(https://www.xing528.com)

这里再次说明：设计码字时要求最大化码字差异矩阵的最小行列式。因此证明：对于任意概率分布的信道，行列式准则都适用。需要指出的是，满足行列式准则并不能保证编码一定是最优的。

对于秩准则和迹准则，由于实际的信道系数（包括信道统计量以及幅度）在推导编码设计准则时并不重要，Yual等人^[408]推导出类似的设计准则如式（3.76）所示。需注意的是，式（3.76）只适用于SNR较大且n趋于无穷的情况。然而，由于每段中继链路都引入了加性噪声，从而使得该设计准则的收敛速度变慢，所以，行列式准则比迹准则更适用些。

采用VAA的传统空时网格码的性能如图3.12和图3.13所示。仿真系统参数与文献[122]中的设置相同，每帧包含130个符号，调制方式为QPSK，无信道编码；通过计算机搜索获得STTC生成矩阵并如Tarohk等人在文献[122]中给出的；一帧时间内信道处于准静态衰落状态。仿真中主要链路服从瑞利分布，而中继链路服从K=4dB的莱斯分布。另外，由于中继链路中引入了加性噪声，导致到达目的节点的数据流SNR降低了一半；尽管如此，STTC性能仍然很好。还需注意的是，对所有可能的码字组合进行遍历搜索可得到很多个满足设计准则的最优编码。Dohler等人^[404]寻找到了稍优于Yuan等人^[408]给出的编码，但两者性能差别很小。

图3.12给出了由两天线的源节点、单天线的目的节点和多个单天线中继节点构成的中继系统采用STTC方案的性能。由于中继等效于VAA的接收天线，因此增加中继数对于获得最大的编码增益具有重要影响；不同状态数的编码方案的性能差别明显，在FER等于1%时SNR差别达0.7dB；另外，对于8状态STTC，具有两个中继节点的VAA方案相比传统的无中继方案有10dB的性能增益。

图3.13给出了8状态不同VAA的STTC性能曲线。值得注意的是，将源节点的发送天线数从2增加到3时，增益仅为1dB。

总而言之，由码字差异矩阵的行列式决定的成对错误概率上界，并不取决于实际的信道衰落统计特性，因此，在瑞利信道下获得的最优化STTC编码同样适用于莱斯、双瑞利，指数-正态或其他衰落类型的信道。需要注意的是，由于此PEP上界并不紧致，所以采用其他设计准则（例如接下来要讨论的准则）有可能获得性能更佳的编码方案。后来Narbar等人^[166]也给出了类似的观点。

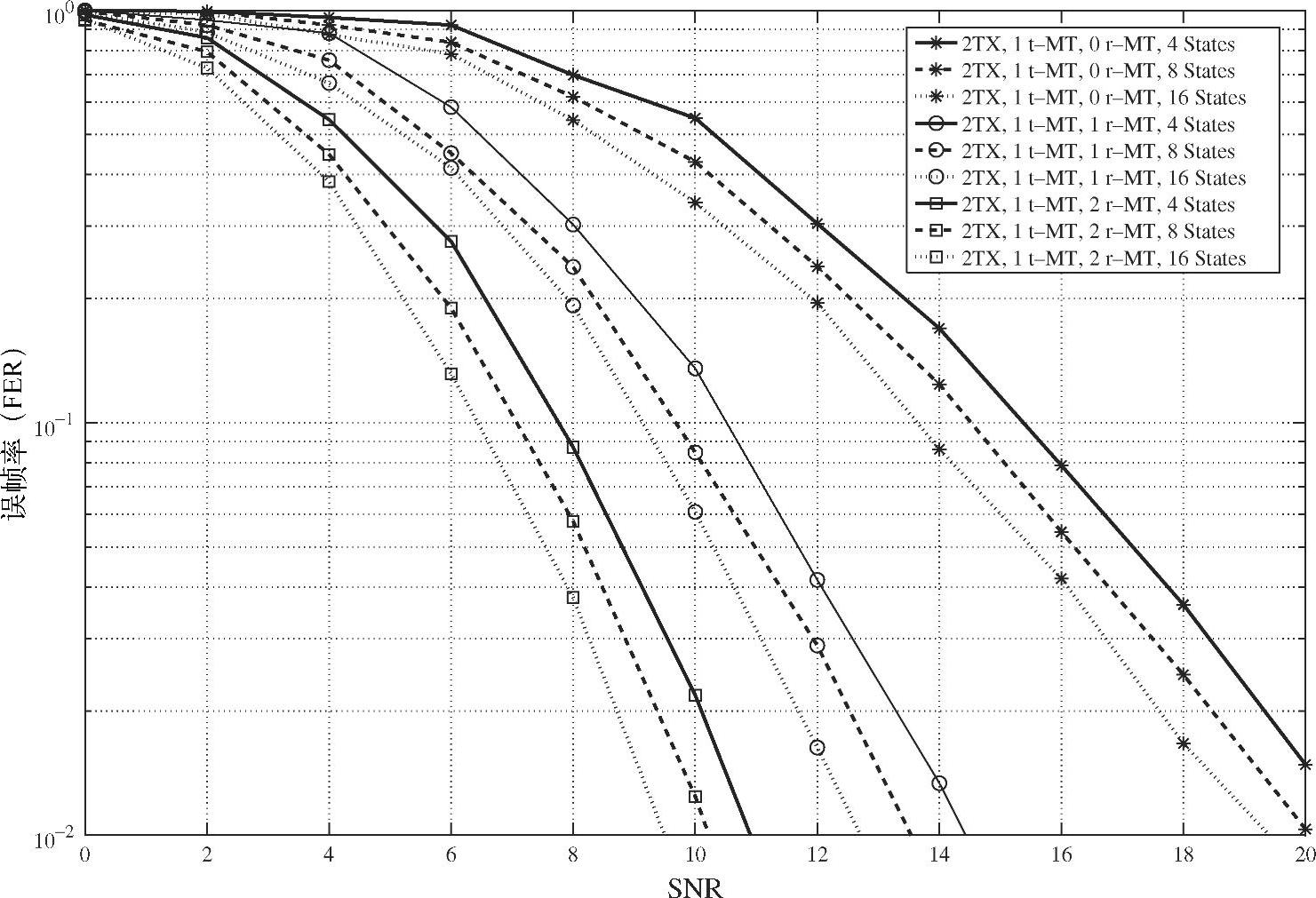
图3.12 两天线源节点、单天线目的节点和多个单天线中继节点

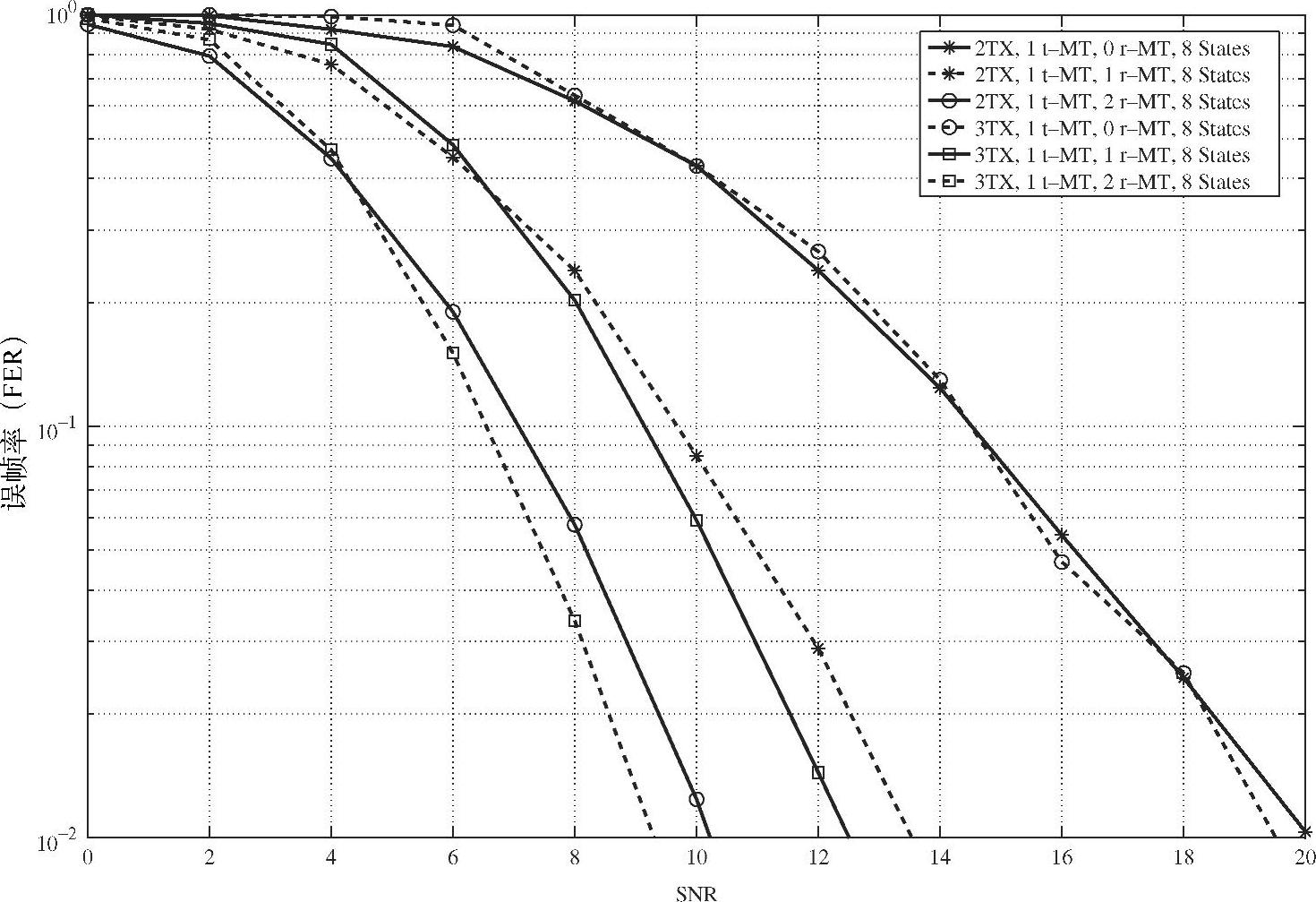
图3.13 两天线/三天线源节点、单天线中继节点和多个单天线目的节点的中继系统

3.3.2.3 特定协议下的设计准则

随后的讨论均遵循Canpolat等人在文献[405]中提出的观点。图3.14是从图3.10中提取的子框图，这里，假设源节点配置一根发射天线，R个中继都配置一根天线，目的节点配置n_r根接收天线。在文献[405]中Canpolat等人分析了文献[166]提出的三种中继协议，事实上这三种协议在中继转发之前均需存储模拟信号，因此都不能算是真正的透明传输。需要说明的是，下面提出的设计准则是在时域中得到的，但同样适用于频域。接下来简要回顾这三种透明中继传输协议：

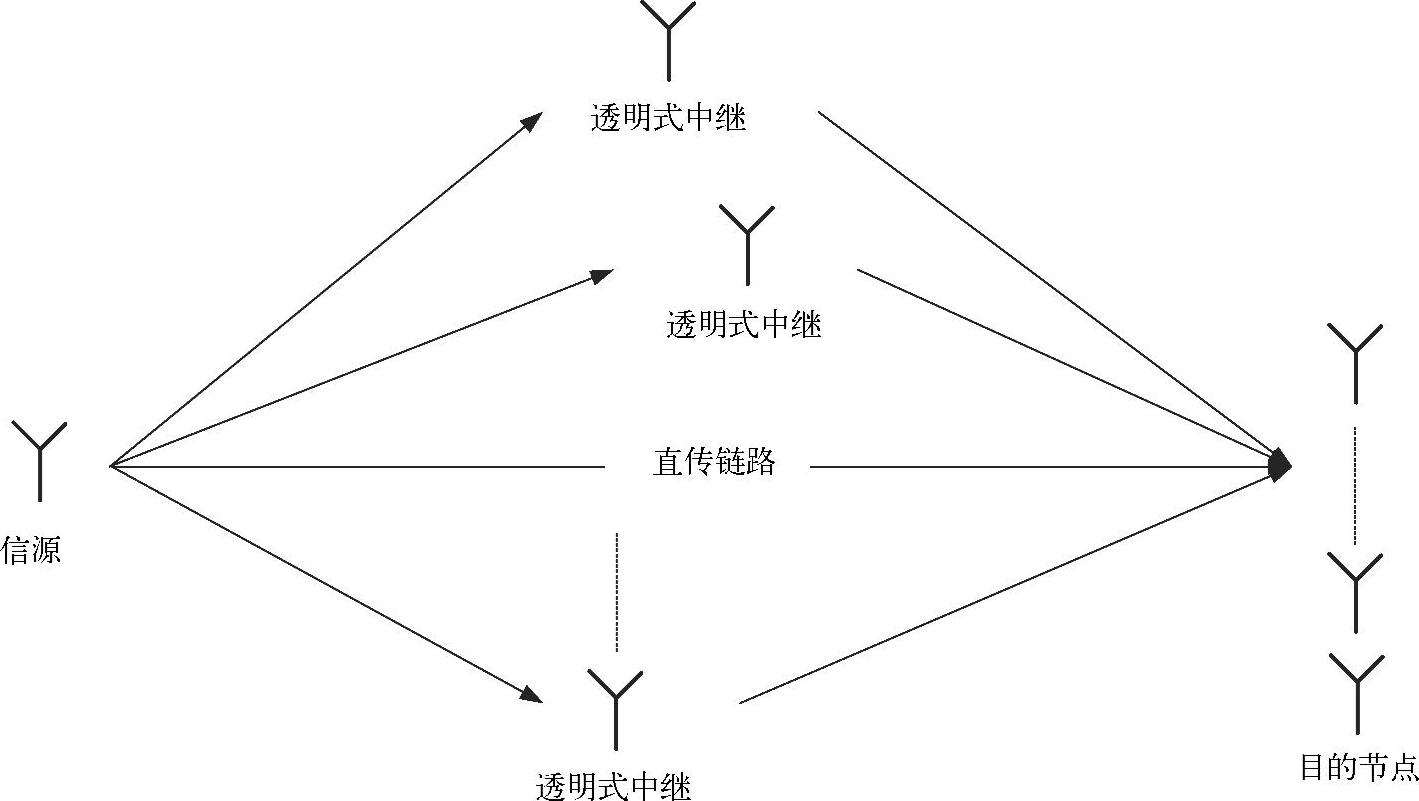
图3.14 透明的空时处理拓扑结构[405]

●协议1源节点先按顺序向R个中继广播M-1个调制符号x₁，x₂，…，x_M-1，每个时隙中只有一个中继接收信号；同时，目的节点接收这M-1个发送符号。第M个时隙，源节点发送第M个符号，所有R个中继节点向目的节点转发它们之前接收到的信号。此协议下，系统容量受限于源到目的节点的直传链路。另外，中继节点存在较多的沉默时期会造成资源浪费。

●协议2协议2与协议1的差别在于，需要每个中继节点在其接收到信号以后的时隙内不断地将其接收到的符号进行重复传输。

●协议3协议3与协议1的差别在于，源节点与目的节点仅在第M个时隙发生通信。当源节点和R个中继节点进行通信时，目的节点可以自由地进行其他的通信传输。

利用联合源节点和中继节点获得的n_t=R+1根发送天线和目的节点的n_r根接收天线，可实现STTC编码。令x^l_m表示第l个信息帧中，由源节点向第m个中继节点传输的STTC编码信号，其中，l=1，2，…，L′，进而可以得到传输总长度为L=M×L′。目的节点第n根接收天线上的接收信号可以用矩阵形式表示为

R_n=H_nX+N_n （3.82）

其中，R_n=[r_n¹r²_n…r^L_n′]表示接收矩阵；X=[x¹x²…x^L′]表示空时矩阵；N_n=[n¹n²…n^L′]表示M×L′维的白高斯噪声矩阵，噪声矢量的每个元素都具有相同的噪声功率。针对不同的转发协议，维度为M×M的信道矩阵可分别表示为

其中，变量γ表示SNR，由于假设各跳具有相同的阴影衰落和路损，则有γ_2，mn=γ_2，m。当接收端采用最大似然（ML）检测时，可以得到平均PEP的上界为

其中，距离度量d²在上述三种中继协议下各有不同的定义。瑞利衰落信道下的三个距离度量分别为

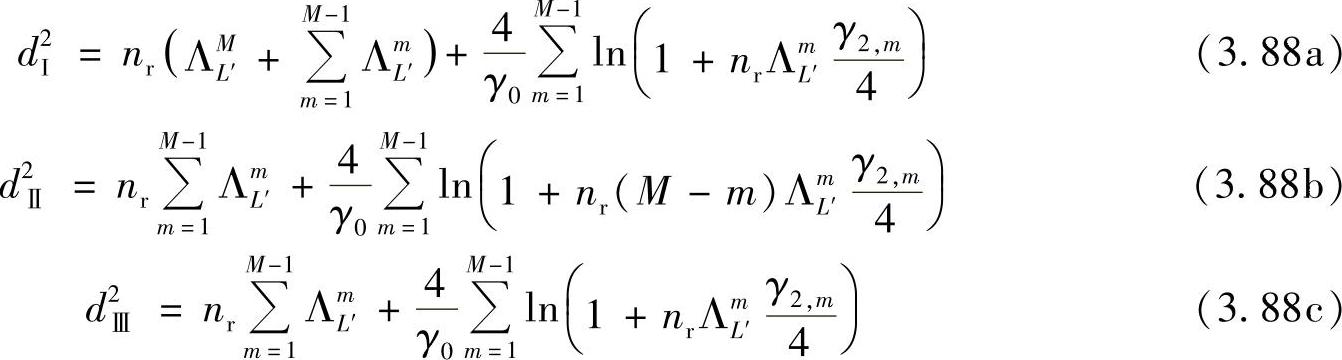
其中，。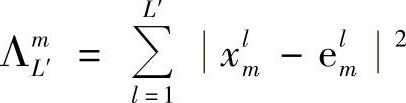

如果假设衰落是确定的，则上述表达式将得到很大的简化，这也是需求合适的STTC设计的基础^[405]。STTC的优势在论文中都有介绍，此处予以省略。值得一提的是，文献[406]中给出了一种改进的可以提供微弱优势的设计准则。