分布式空时分组码技术简介

对于一般的无线中继网络，乘载着相同信息的信号经过不同的噪声干扰形成了不同的副本，被不同的中继接收到，中继对接收信号进行处理并将信号转发至目的节点。不同中继节点上分布式的处理就形成了VAA。将传统的空时编码应用到中继网络可获得协同分集和编码增益。采用透明中继转发协议或再生中继协议可以构造分布式空时编码，当然，两种协议下的编码设计方法有较大区别。

在本节中，我们主要讨论基于透明中继转发协议的分布式空时分组码设计，而基于再生中继协议的分布式空时分组码设计将在下一章中讨论。针对透明空时分组码的研究文献非常之多，例如文献[295，318，336，338，342，367，384-401]。由于其优异的性能，我们仅讨论Hassibi等人提出的设计方案文献。

3.3.1.1 分布式线性扩散空时码

本节将研究Jing和Hassibi提出的基于线性扩散码的分布式空时编码（DLD-STC）。在DLD-STC中，每个中继节点在收到来自源节点的信号后，对接收到的T个信号进行线性变换，然后所有中继同时将线性变换后的信号转发给目的节点。天线集中放置的MIMO系统中的线性扩散码^[402]与中继网络中的DLD-STC^[403]的主要差异有两方面：首先，在MIMO系统中，由于所有天线在空间上是集中放置的，因而线性扩散码的设计是集中式的，而在无线中继系统中，中继节点在空间上是分散的，因此DLD-STC的设计只能是分布式的；其次，MI-MO系统中发射天线完全已知要发送的信息信号，而在中继网络结构中，每个中继收到的是存在干扰的原始信息副本。因此，上述两个方面的差异导致了DLD-STC和传统的线性扩散码在设计时存在差异。

下面，我们考虑由1个源节点，n个中继节点，1个目的节点构成的常规两跳中继系统。为了分析方便，假设源节点与目的节点之间不存在直传链路。图3.11给出了DLD-STC的系统框图。发送符号序列为S=（s（1），…，s（T））^T，其中s（k）表示第k个信息符号，并假设发送符号能量归一，即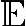{s（k）2}=1。整个传输过程可分为两个阶段：首先，在前T个时隙源节点以发射功率p_S向所有中继节点广播信息符号序列S。第i个中继接收到的信号yⁱ_SR为

其中，hⁱ_SR表示源节点到第i个中继的信道的衰落系数，假设衰落系数在这T个时隙内保持不变；nⁱ_SR为第i个中继的接收噪声向量，其每个元素是零均值双边功率谱密度为N₀/2的复高斯随机变量。

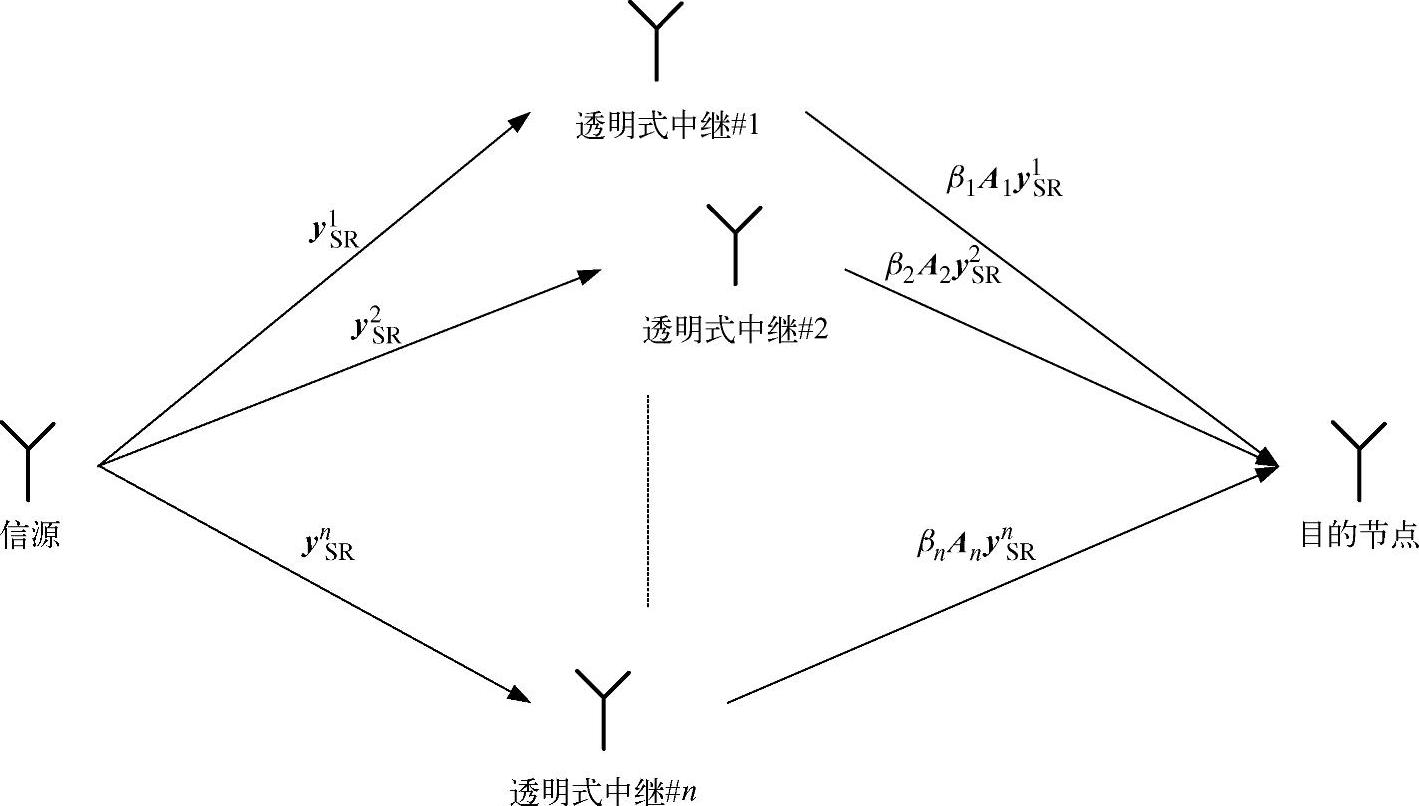
图3.11分布式线性扩散空时码的系统框图

DLD-STC系统中，每个中继对接收信号进行线性变化：

其中，A_i为第i个中继节点T×T阶的线性变化矩阵，表示为

矩阵A_i的第j列A_i，j表示为

线性变化矩阵A_i可以是任意的矩阵。为了方便分析，假设A_i是一个酉矩阵，即满足（A_i）^HA_i=I。中继将线性变化后的信号矩阵Xⁱ乘以归一化因子β_i得到Xⁱ_R后将其转发至目的节点

这里，功率放大因子β_i满足以下条件

其中，p_R是中继发射功率。为了便于分析，我们考虑中继发送端进行的是长期功率限制，而不同于其余章节中考虑的短期功率限制，即式（3.40）只对噪声作统计平均。在长期功率限制下，分别对噪声和信道衰落进行统计平均，则式（3.40）可进一步表示为

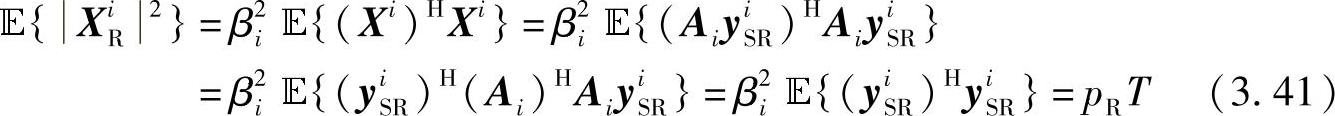
将式（3.35）代入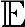{（yⁱ_SR）^H（yⁱ_SR）}，可得

再将上式代入式（3.41）可得

根据式（3.43）可计算出相应的功率放大因子为

目的节点的接收信号是所有中继转发信号的叠加，即

其中，n_D是目的节点的接收噪声向量，而等效噪声矢量为

这里等效噪声的方差为

式（3.45）可进一步表示为

其中，

从式（3.46）可知，是n个复高斯随机向量的线性组合，因而也满足复高斯分布，相应的PDF为

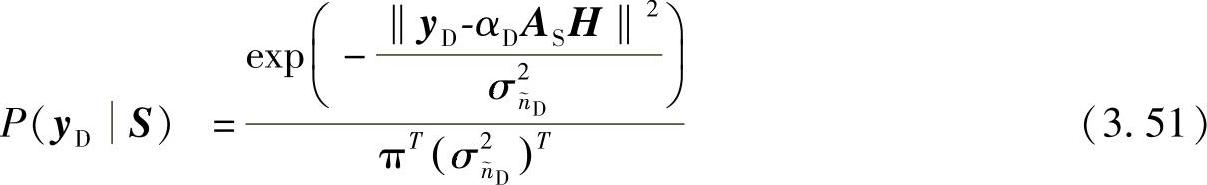
其中，‖x‖表示向量x的F范数。目的节点对DLD-STC采用最大似然译码检测，从而使P（y_D|S）最大化：

在后续章节中，我们将分析DLD-STC系统的成对错误概率（PEP）。

3.3.1.2 通信系统的Chernoff界

首先，我们简短回顾一下一般通信系统的Chernoff界的计算，并由此推导出DLD-DTC系统的PEP上界。对于一个任意给定的随机变量z和函数f（z），f（z）满足以下条件：

如果变量z的各阶统计量都存在，那么Chernoff界使得下列不等式成立：

P（z＞0）≤{f（z）} （3.54）

例如，若f（z）=exp（λz），Chernoff界就可表示为

P（z＞0）≤{exp（λz）} （3.55）

考虑一个点到点单天线通信系统，其接收信号为

y=hs+n （3.56）(www.xing528.com)

其中，s是发送信号；h是信道衰落系数；n是单边功率谱密度为N₀的高斯随机噪声；接收端采用最大似然（ML）译码可得

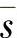采用ML检测，译码器选择与接收信号距离最近的星座符号。用P（，h）表示发送符号为s而译码器错判为的概率，即

对上述等式应用Chernoff界公式（3.55），可得

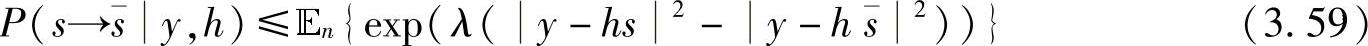
其中，E_n{·}表示对随机变量n的期望。经代数变换，式（3.59）可表示为

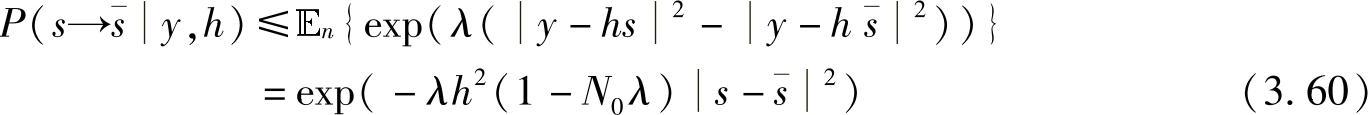
当时式（3.60）取得最小值，从而式（3.60）可表示为

类似地，在多天线空时编码系统中，假设用S表示传输码字矩阵，相应的接收信号矩阵可表示为

Y=HS+N （3.62）

其中，H={h_ij}是信道矩阵；h_ij表示第i根发送天线到第j根发送天线间的信道衰落系数；N是随机噪声向量，其成员元素是维度功率谱密度为N₀的复高斯随机变量。

采用与单天线系统相同的计算方法，多天线空时编码系统发送空时码字S，但译码器错判为的PEP上界为

其中，H^H表示矩阵H的共轭转置。

3.3.1.3 分布式线性扩散空时码的条件错误概率上界

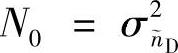在本节中，我们利用Chernoff界推导DLD-STC系统的PEP上界。如前所述，同样假设服从高斯分布，其均值为0，方差为。将和S=

代入式（3.63），则DLD-STC系统的PEP上界为

对上式的hⁱ_SR2求平均，可得^[403]：

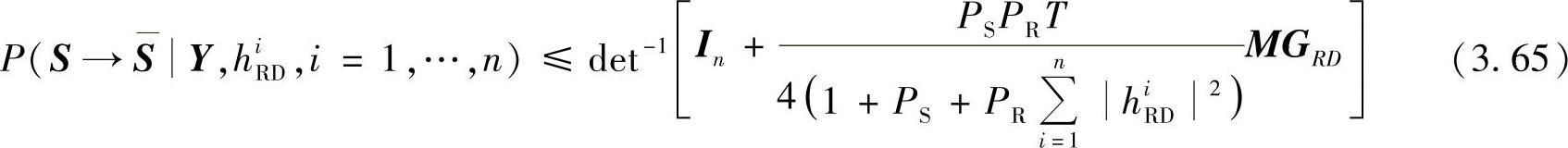
其中，G_RD=diag{h¹_RD，…，hⁿ_RD}。这里，diag{x¹，…，xⁿ}表示对角元素为x¹，…，xⁿ的对角矩阵。

将上式所示的DLD-DTC的PEP上界与多天线系统的PEP的Chernoff界对比，我们发现两者相似，但上式还含有随机变量|hⁱ_RD|²，i=1，…，n。为了求得最终形式的PEP上界表达式，还需对式（3.65）中的|hⁱ_RD|²，i=1，…，n进行统计平均。由于很难求得对所有|hⁱ_RD|²求期望的闭式解，我们采用近似的方法。定义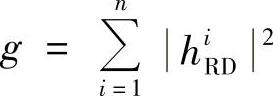，它服从伽玛分布^[403]：

随机变量g的均值和方差均为n。当n比较大时，g可由其均值近似，即g≈n^[403]。因此，式（3.65）可以近似为

当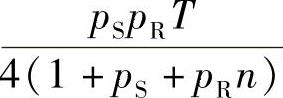取最大值时，上式达到最小值。用P=P_S+P_Rn表示源节点和所有的n个中继节点的总发射功率，即有

上式达到最大值的条件为

P_S=P/2 P_R=P/2n （3.69）

因此，最优的功率分配策略是总发射功率的一半分配给源节点，另一半发射功率分配给所有的中继节点。将式（3.69）代入式（3.67），可得

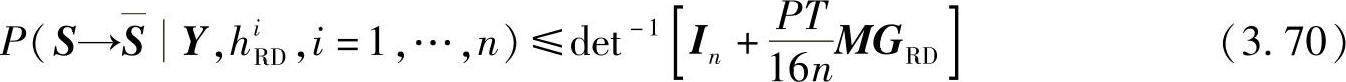
假设矩阵M满秩，且有T≥n，对上式中的|hⁱ_RD|²求平均，则DLD-DTC系统的平均PEP可进一步近似为

从式（3.71）可见，如果矩阵M满秩，且有T≥n，则DLD-STC系统可获得的分集度为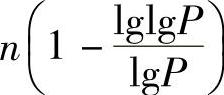。当发射功率P很大时，有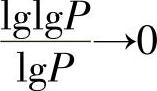，因此，在高SNR区域可获得的分集度为n。通常，DLD-STC的分集度取决于总发射功率P。上式中我们假设有T≥n。通常情况

下，DLD-DTC系统可获得的分集度为min{n，T}

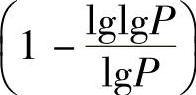。为了获得最大的编码增益，需最大化矩阵M的行列式。

对比DLD-STC系统和采用STTC的多天线系统的平均PEP表达式，如3.3.2节和文献[122]所示，高信噪比下，STTC系统的PEP上界可以近似为

将上式与式（3.71）所示的DLD-STC的PEP相比，可得到以下结论：在相同的BER和功率条件下，与STTC相比，DLD-DTC存在（3+10log₁₀logP）dB的SNR损失，其中3dB的性能损失是由中继节点的发送功率只占总功率的一半，造成以而10log₁₀logP表征的是DLD-STC系统相比于STTC系统的分集度损失，这是由中继节点接收信号中存在的残留噪声造成的。如在第1、2章所述，上述功率损失可以通过路损和/或阴影增益得到补偿。

类似地，在低SNR区域，发射功率P＜＜1，DLD-DTC的平均PEP的上界可以近似为

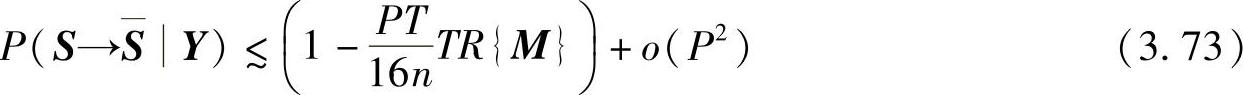
其中，TR{M}表示矩阵M的迹。从上式可以看出，在低发射功率下，编码增益是由编码矩阵M的迹所决定的，为获得最大编码增益就需要最大化编码矩阵M的迹。

基于以上讨论，可以总结出中继系统中分布式线性扩散空时码的设计准则：

定理3.3.1：对于一个有n个中继节点的DLD-STC系统，令A_i表示第i个中继的线性

扩散矩阵，则该系统所能获得的最大分集度为min{n，T}

。高信噪比时的编码增益取决于码字差异矩阵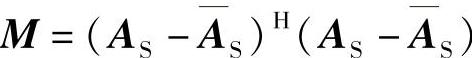的行列式，其中A_S=[A₁S，…，A_nS]。为了优化系统在高信噪比时的性能，需要最大化差异矩阵M的行列式。低信噪比时的编码增益取决于码字差异矩阵M的迹，因此，为了在低SNR时具有最优的性能，需要最大化差异矩阵的迹。