多分支多跳中继放大转发优化

目前，针对多分支多跳转发放大系统的研究还较少，但前面讨论的大部分技术都可以很容易地拓展到这种具有一般性的拓扑结构。文献[275，333，355]专门研究了此拓扑结构。

3.2.4.1 系统假设

图3.7描述了多分支多跳拓扑结构，其主要特征总结如下：

●L分支N跳的拓扑结构。

●存在源节点到目的节点的直传链路。

●采用固定或自适应的转发放大因子。

●考虑无阴影衰落的平坦Nakagami-m衰落。

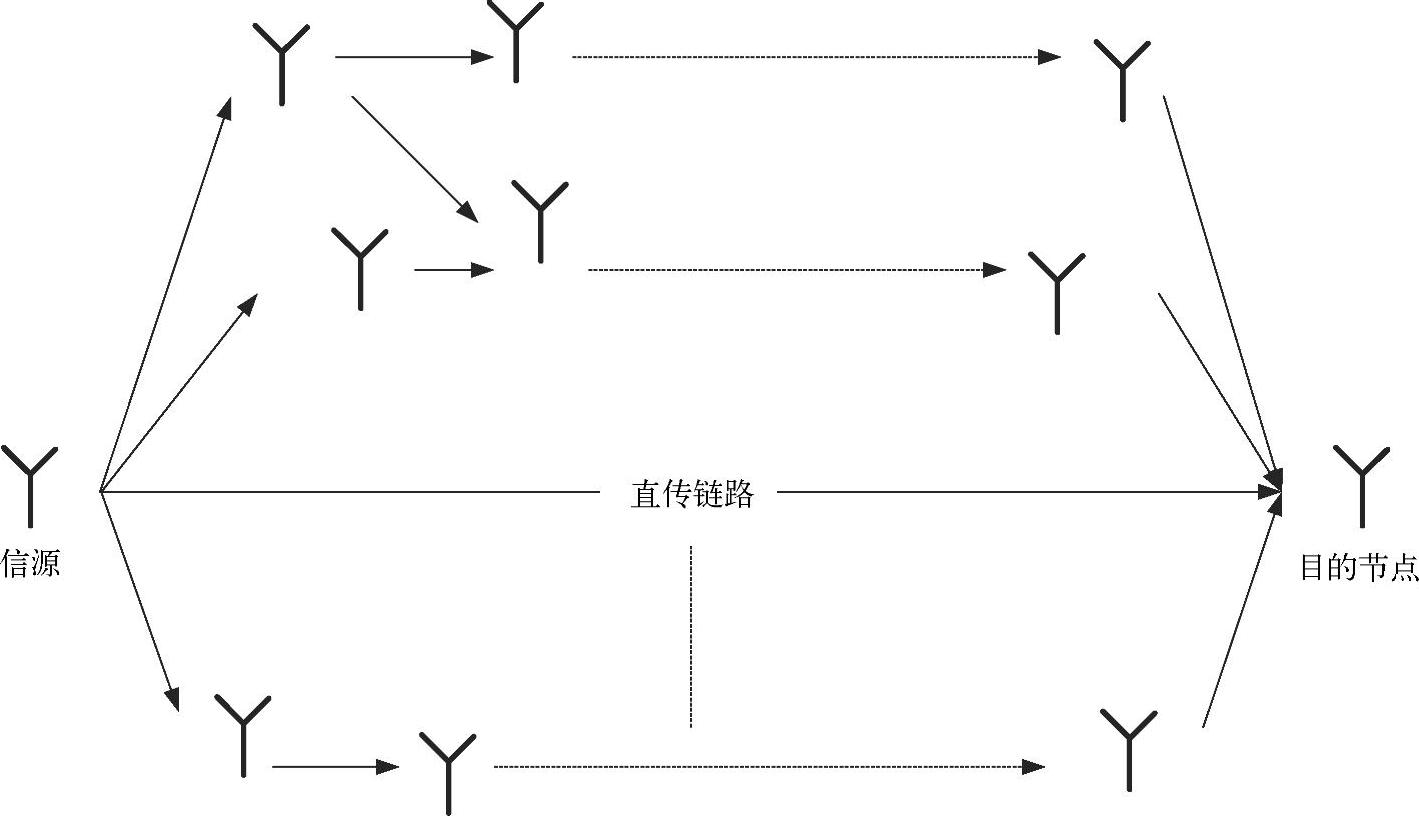
图3.7 典型的多分支多跳的拓扑结构（有直传链路、无阴影衰落的平坦瑞利衰落）

假设N跳链路之间和L分支之间都不存在干扰，可通过在时域、频域、码域分配不同的资源来实现正交的传输。

我们首先考虑具有多分支多跳拓扑中每个节点配置单天线的情况，然后扩展到节点配置多根天线的情况。

3.2.4.2 SISO模式

Ribeiro在文献[275]中提出：式（3.5）中积分很快收敛到零。图3.8比较了对于归一化瑞利分布P_b（e|γ）=Q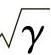（）在不同平均信噪比下的PDF。很显然随着平均信噪比的增加，Q函数很快收敛到0。这意味着曲线下方的大部分面积都是低SNR部分，这就可使用麦克劳林级数展开来大大简化式（3.5）中的积分表示及其相应的结果。当γ足够大时，PDF可用麦克劳林级数的第一项近似表示，文献[383]给出了严格意义上的近似表达式，即有p_γ（γ）→aγ^t+ο（γ），因此，SEP的渐进表达式可简单地表示为

其中，a和t取决于信道类型。例如，对于Nakagami-m信道，a=m^m/Γ（m），t=m-1；对于Rice-K信道，a=（1+K）exp（-K），t=0。利用这些结论，就可以推导出通用中继系统在衰落信道下的端到端SEP的渐进表达式。

例如，源节点和目的节点之间存在直传链路的两跳单分支中继拓扑结构在信噪比足够高时，上述的式（3.29）以及式（3.26）所示的转发链路的渐进SNR表达式均成立。Ribeiro等人^[275]根据式（3.29）进一步推导了通用拓扑结构下端到端SEP的通用且简单的近似表示：

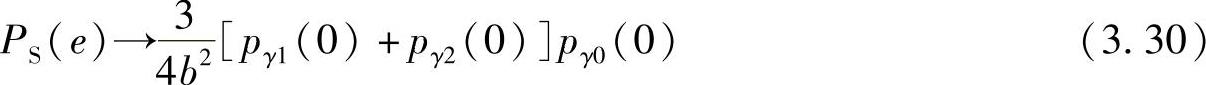
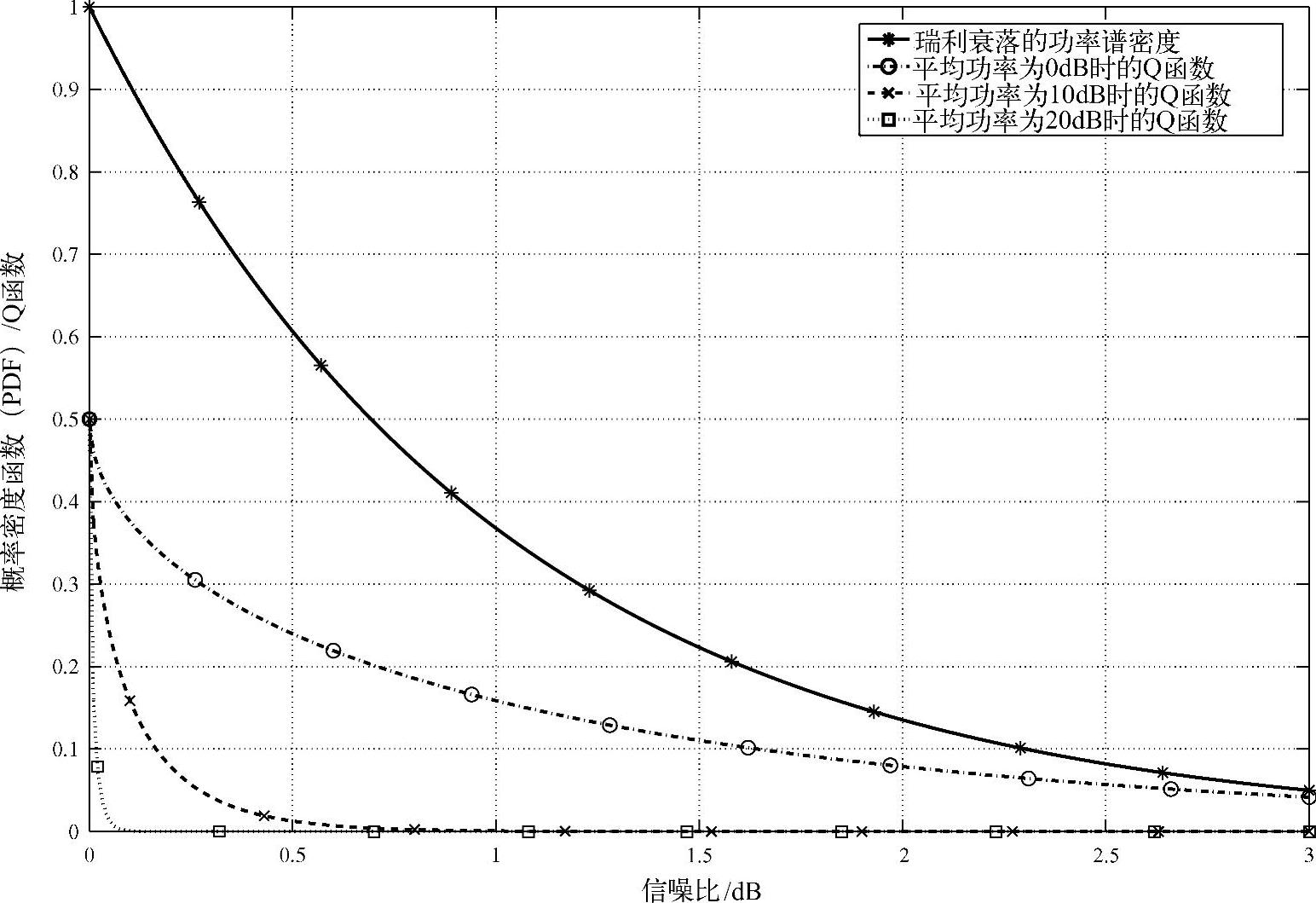
图3.8 瑞利衰落的概率密度曲线和不同的Q函数实现(www.xing528.com)

利用在第2章给出的Rician-K的PDF，SEP的渐近表达式为

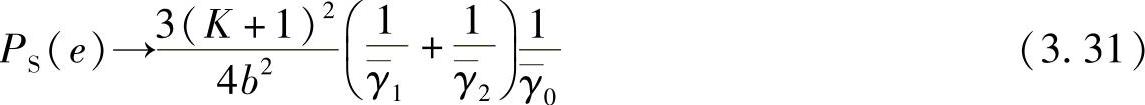
在图3.7所示的一般中继拓扑结构的场景下，文献[275]给出了SEP的表达式为

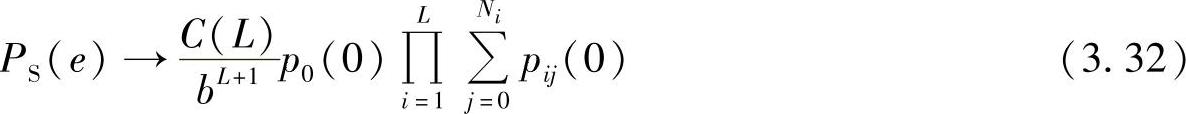
其中，C（L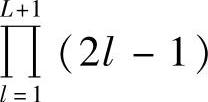）=（）/（2（L+1）！l^（L+1））；p₀（0）和p_ij（0）分别表示直传链路和第j跳第i分支的功率PDF在零点处的展开；N_i是第i分支的跳数；b是由调制方式所确定的常数。文献[275]表明，上述渐进表达式在所关心的误码范围内有很高的精度。

3.2.4.3 MIMO模式

将SISO拓扑扩展到每个节点配置多根天线的MIMO场景时有许多有趣的应用。为了方便介绍，我们只分析单分支两跳SIMO系统的拓扑结构，如图3.9所示。遵循Mheidat和Uysalde^[333]的分析，我们将分为固定与可变的放大转发系数两种放大转发策略进行分析，且仅考虑噪声功率和发射功率在两转发阶段不变的情况，即有γ₁=γ₂=γ。

针对全盲或半盲中继，文献[333]给出了固定转发放大系数且采用MPSK调制方式下的SEP及其上界的表达式：

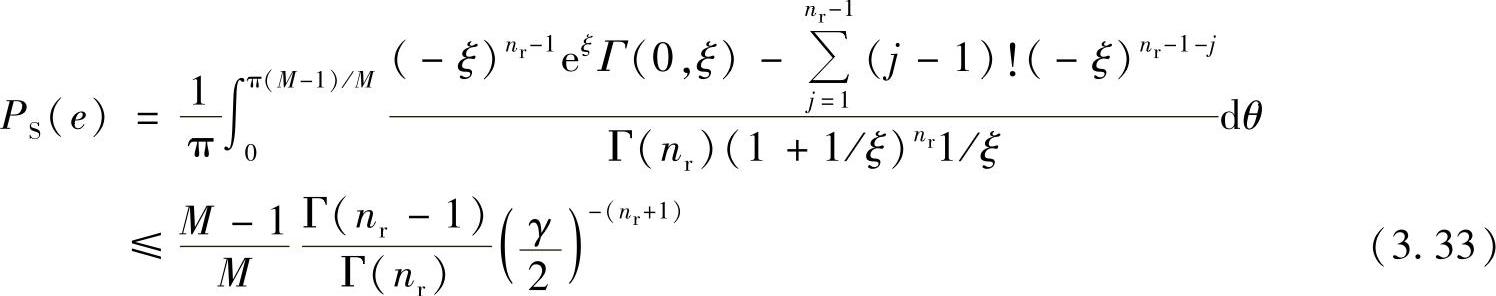
其中，n_r表示目的节点的接收天线数；ξ=sin²θ/（sin²（π/M）γ）；Γ（*）是伽玛函数，Γ（*，*）是高阶不完整伽玛函数。从SEP上界表达式可以得到固定放大转发系数方案下的分集度为n_r+1。

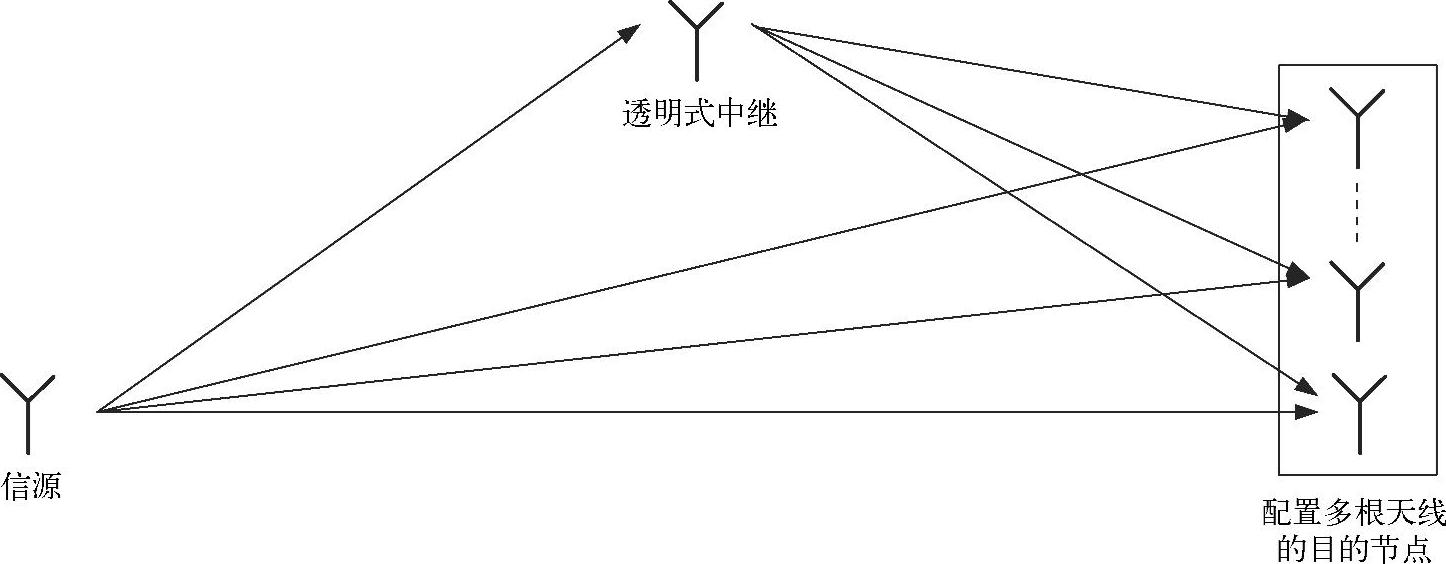
图3.9 典型的单分支两跳SIMO系统的拓扑结构（有直传链路，无阴影衰落的平坦瑞利衰落）

对于信道状态信息辅助中继采用可变的放大系数时，在MPSK调制方式下的误符号率SEP的精确表达式及其上确界可表示为[333]

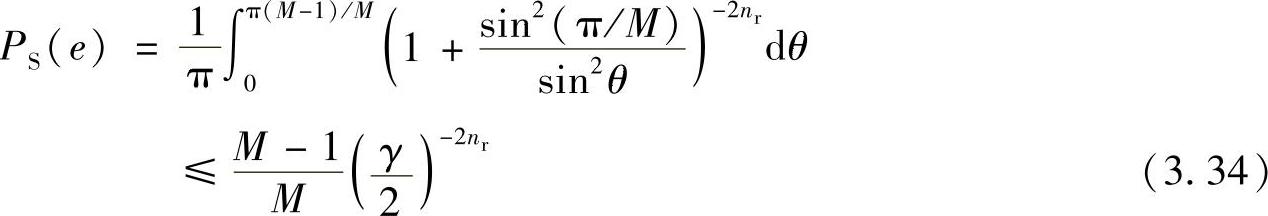
此时可获得的分集度为2n_r。

对比两种放大转发模式可知，仅当中继采用可变的放大系数时才能获得满分集度2n_r。类似的结论对于一般的MIMO中继拓扑结构也成立。