多分支两跳中继放大转发优化方案

目前，关于多分支两跳中继转发放大协议的研究已有很多^{[272，235，333，360，373]}。这里，我们仅讨论全盲与半盲中继^[360]，以及信道状态信息辅助（CSI-assisted）中继^[272，373]。

3.2.3.1 系统假设

图3.5给出了系统的拓扑结构、其系统特征总结如下：

●两跳L分支的拓扑结构。

●存在源节点到目的节点的直传链路。

●采用固定或可变的转发放大系数。

●考虑无阴影衰落的平坦Nakagami-m衰落信道。

图3.5 典型的多分支两跳拓扑结构（有直传链路、无阴影衰落的平坦瑞利衰落）

假设在此拓扑结构中，L条分支路径不存在相互干扰，可通过在时域、频域、码域分配不同的资源，使传输过程保持正交。

此外，目的节点可采用最大比合并（MRC）算法对所有分支的接收信号进行合并处理，也可采用选择合并（SC）算法选择最优的分支进行处理，相应的端到端的接收信噪比可表示为

其中，γ₀表示直传链路的信噪比；γ_l表示第l个分支路径的信噪比。

我们仅考虑算法，而SC算法的分析类似，这里不再讲述。首先考虑中继节点采用固定转发放大系数的情况，即针对全盲和半盲中继类型，然后讨论中继采用自适应的放大转发系数以弥补信道衰落的情况，即针对信道状态信息辅助（CSI-assisted）中继类型。

3.2.3.2 全盲和半盲中继

全盲和半盲中继类型下，第l分支的信噪比γ_l为

前面章节针对两跳和多跳中继链路推导所得的PDF、CDF和MGF表达式，在逐分支分析时都可被利用，为了简单起见，在此不再重复。假设各分支间彼此独立，端到端信道的MGF可写为

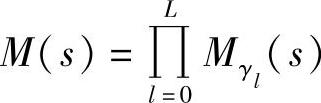(www.xing528.com)

由此可推导出不同性能的闭式表达式或者简单的积分表达式^[91]。DiRenzo等人^[360]给出了上述表达式的界，从而适应于非整数阶Nakagami-m衰落信道以及Weibull衰落分布的场景。

3.2.3.3 信道状态信息辅助的中继

基于文献[276]和[373]，我们分析信道状态信息辅助中继情况下的系统性能。采用可变的中继放大因子，第l分支的端到端信噪比可表示为

文献[279]和[373]分别给出了这种情况下的PDF、CDF和MGF表达式：

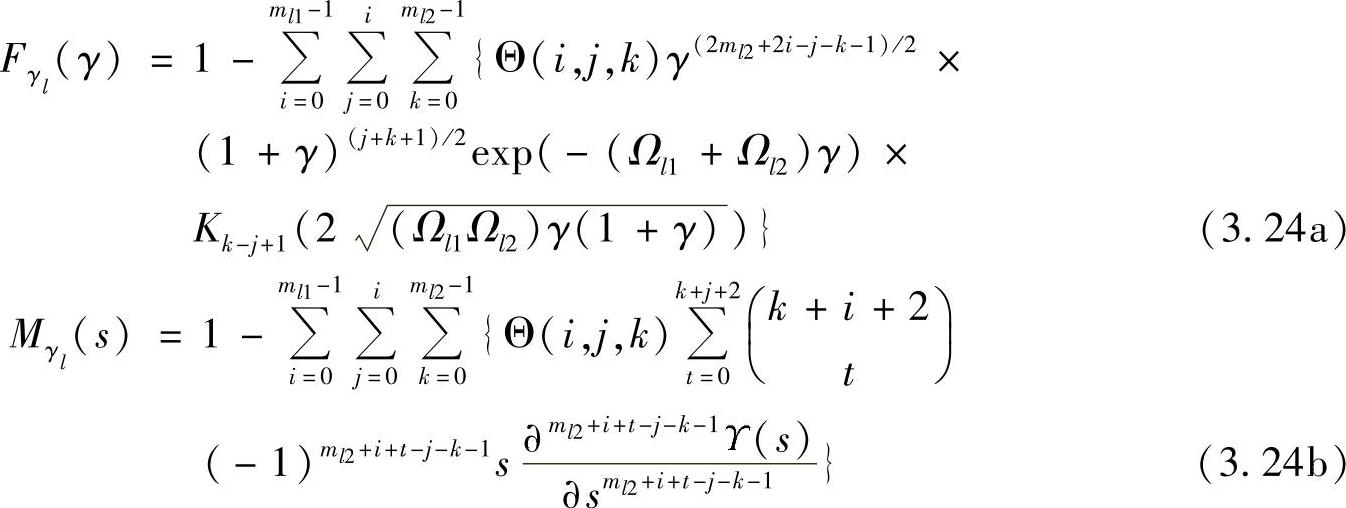
其中

K_v（·）是第二类v阶修正贝塞尔函数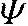；（·；·；·）是合流超几何函数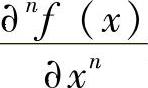；表示函数f（x）的关于x的n阶导，注意=f（x），函数求导可利用一些专用的数学软件。

为了便于分析，Anghel和Kaveh给出了瑞利衰落下的上界和下界。当信噪比较高时，中继节点上的噪声可以忽略，式（3.23）可简化为

通过对中断概率进行求导可得到MGF，但是由此获得的误符号率（SEP）的表达式中包含着难以处理的积分。Anghel和Kaveh推导了MPSK调制方式下SEP的渐进紧致上界和下界：

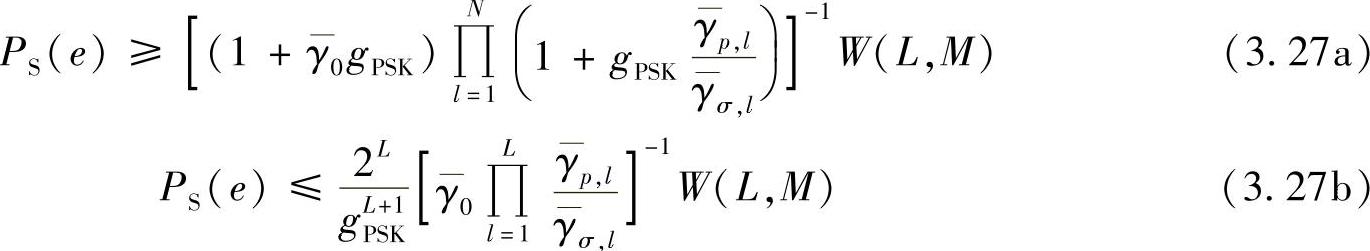
其中，g_PSK=sin²（π/M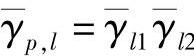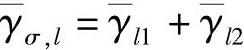）；；，且

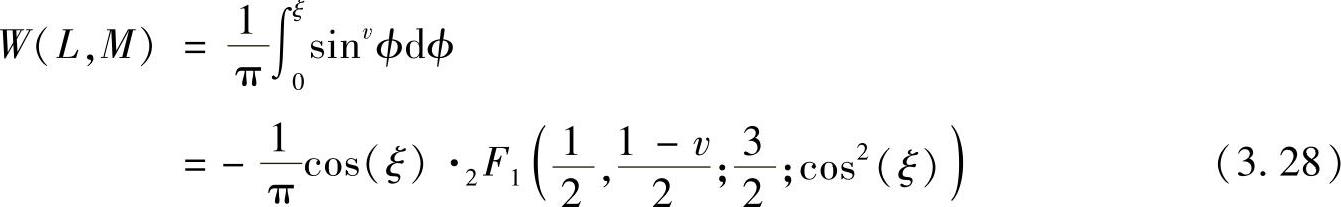
其中，ξ=π（M-1）/M；υ=2L+2，₂F₁（.，.；.；.）是高斯超几何函数。图3.6给出了采用QPSK调制、路损因子为组中继节点，位于源节点和目的节点中间位置时SER的上界和下界的紧致性。可以发现，在中继分支数量较少时，SEP具有紧致的上界和下界，而随着分支数的增加，上界和下界越来越宽松。

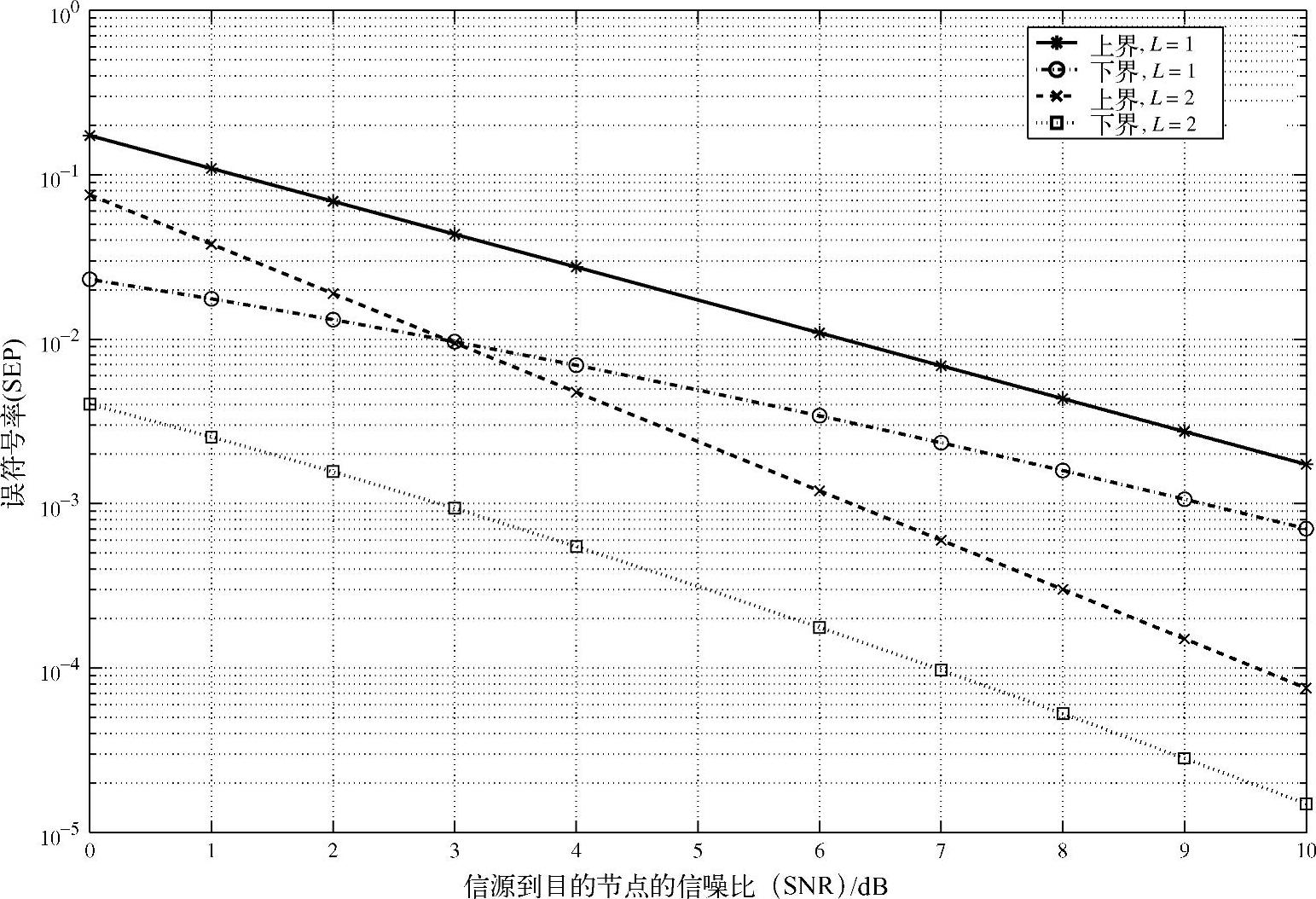
图3.6 不同分支数时误符号率的上界和下界