本节将上面两跳的网络拓扑结构扩展到多个串行级联的中继节点构成的多跳结构,尽管这方面的文献较少,但可以利用3.2.1节的方法来对单分支多跳拓扑结构进行分析。文献[168,276,326,327]就给出了一种推导端到端信噪比(SNR)以及误码率的方法。
3.2.2.1 系统假设
图3.4描述了单分支多跳网络拓扑结构,其主要特点如下:
●单分支N跳的网络拓扑结构。
●不存在直传链路。
●固定的放大转发增益系数。
●无阴影衰落的平坦Nakagami-m衰落信道
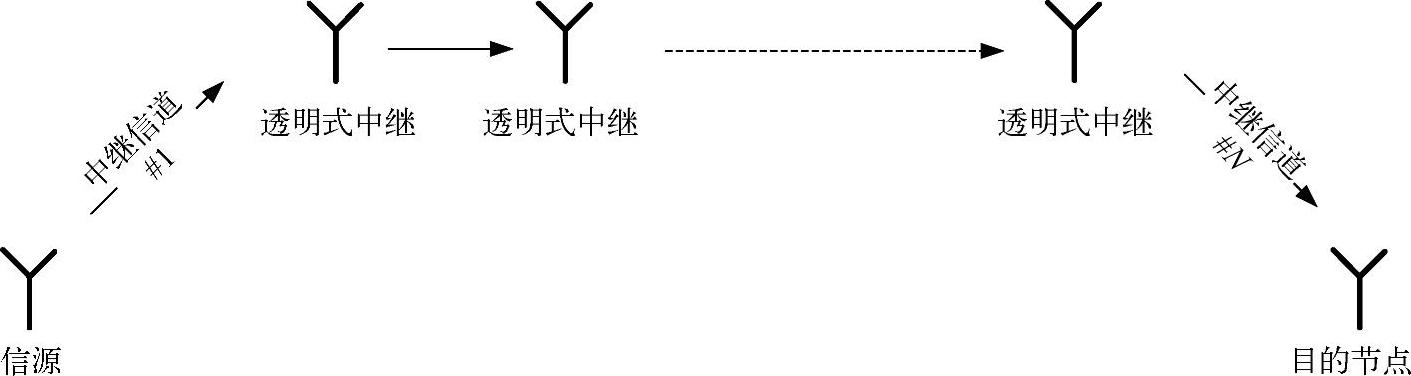
图3.4 典型的单分支多跳拓扑结构(无直传链路、无阴影衰落的平坦瑞利衰落)
考虑系统中有N个转发节点。假设源节点到目的节点不存在直传链路,从而形成了源节点到目的节点的单分支拓扑结构。进一步假设中继节点只知道前一个转发节点的平均衰落功率,对于信道状态信息辅助(CSI-assisted)盲中继而言,以下的分析结论同样适用。同样,我们先分析瑞利衰落场景,即参数m=1,然后推广到一般性的Nakagami衰落场景。
3.2.2.2 瑞利衰落信道
按照文献[168,273,276]的分析方法,当中继节点采用固定的中继转发放大系数时(即半盲型中继),接收机上端到端的信噪比可以表示为

对于瑞利衰落信道,当i≥1,且C0≥1时[168]

由式(3.13)可以导出闭式解,并在文献[168,274,276]中给出了上界。注意到式(3.13)表征的是调和平均,而其上界是其几何平均,因而式(3.13)可简化为(https://www.xing528.com)

利用文献[276]的推论,可以得到端到端接收信噪比上界的PDF和CDF。CDF可以表示为
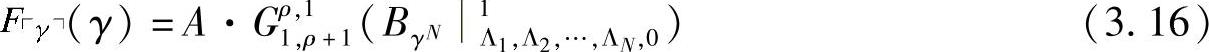
其中,
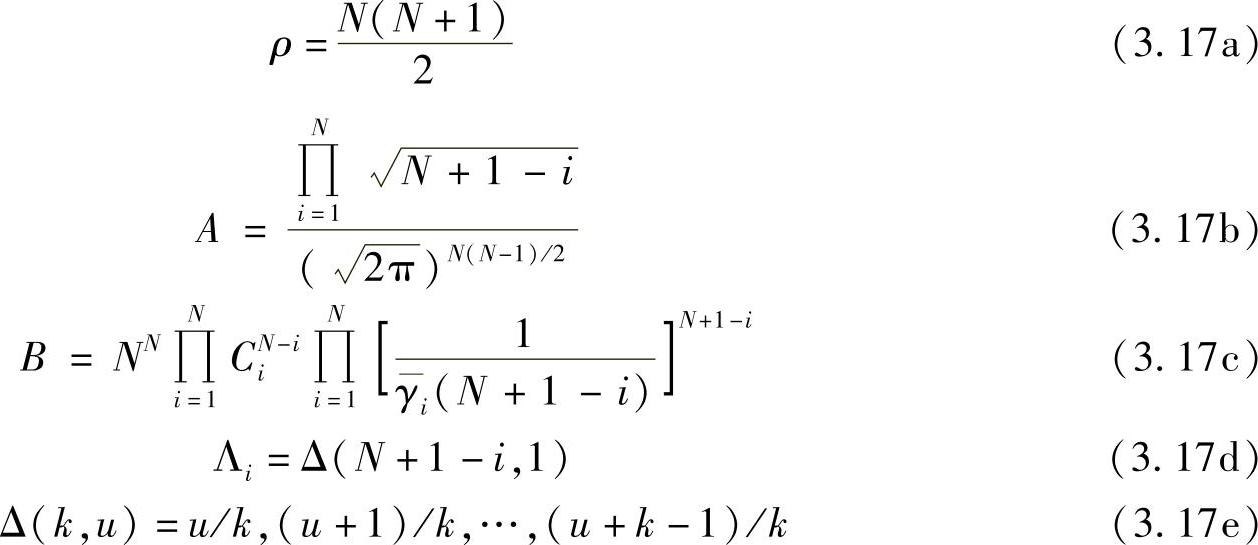
代入式(3.6),可以得到错误概率的下界[276]:
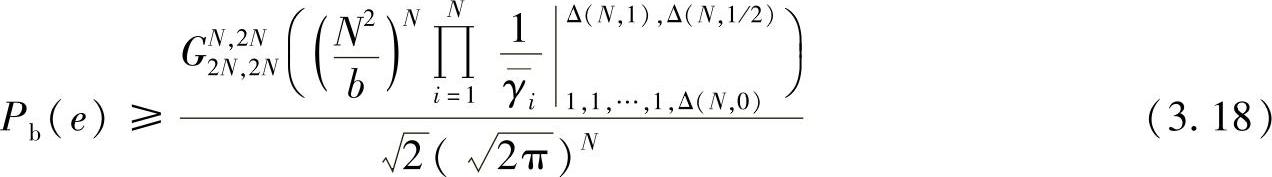
文献[276]中的结果表明,虽然该下界并非渐近紧致界,但在我们所关心的错误性能范围内该结果已经足够精确了。随后Karagiannidis利用Pade近似理论推导了端到端接收信噪比上界的高阶矩,从而获得了更精确的错误概率。
3.2.2.3 Nakagami衰落信道
对于Nakagami-m衰落信道,可采用类似于瑞利信道下的分析方法,因此我们在此只给出PDF、CDF和BEP的表达式:
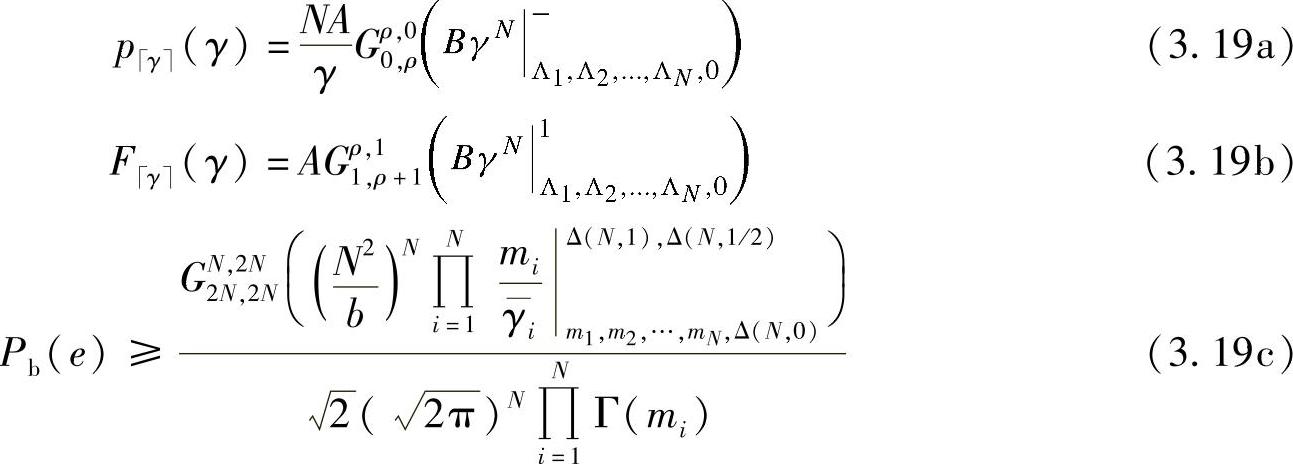
其中
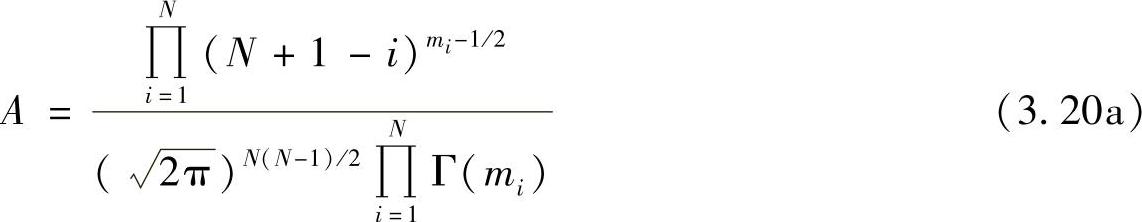
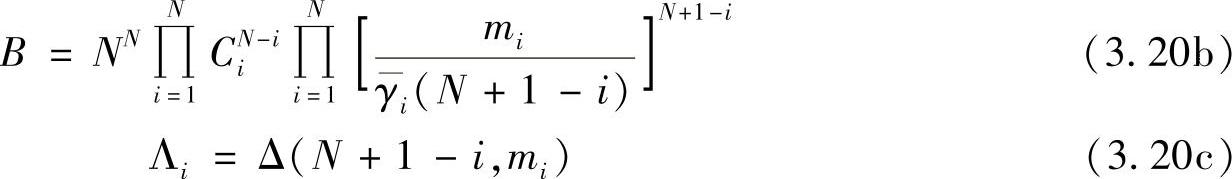
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




