透明中继信道的小尺度衰落特性讨论

下面简要介绍一下透明协同信道的重要特性，包括路损、阴影效应和衰落等。

2.4.1.1 路损

围绕透明中继信道的路损特性，存在着两个重要变化：转效点特性的变化和路损的增加。

（1）转效点特性的变化

正如2.3节中所说，降低发送和接收天线的高度将会减小信道转效点距离，因此传统信道和协同信道的转效点距离有所不同。当天线高度降低以及中继段耦合两方面因素一并出现时，将使信道的路损特性变得非常复杂。通过应用式（2.15），我们可以针对具体的路损模型量化得到其路损特性。下面通过图2.30举例说明路损和转效点距离之间的关系。在图2.30中，分别讨论发送和接收端之间是中继信道还是非中继信道的情况。假设两种情况下传统信道的转效点距离都是100m，中继信道的转效点距离为10m。无论何种情况，转效点前的路损系数n₁=2，转效点后的路损系数n₂=4。可以从式（2.15）和多种转效点距离中看出，要得到转效点的整体特性其过程将是非常复杂的。

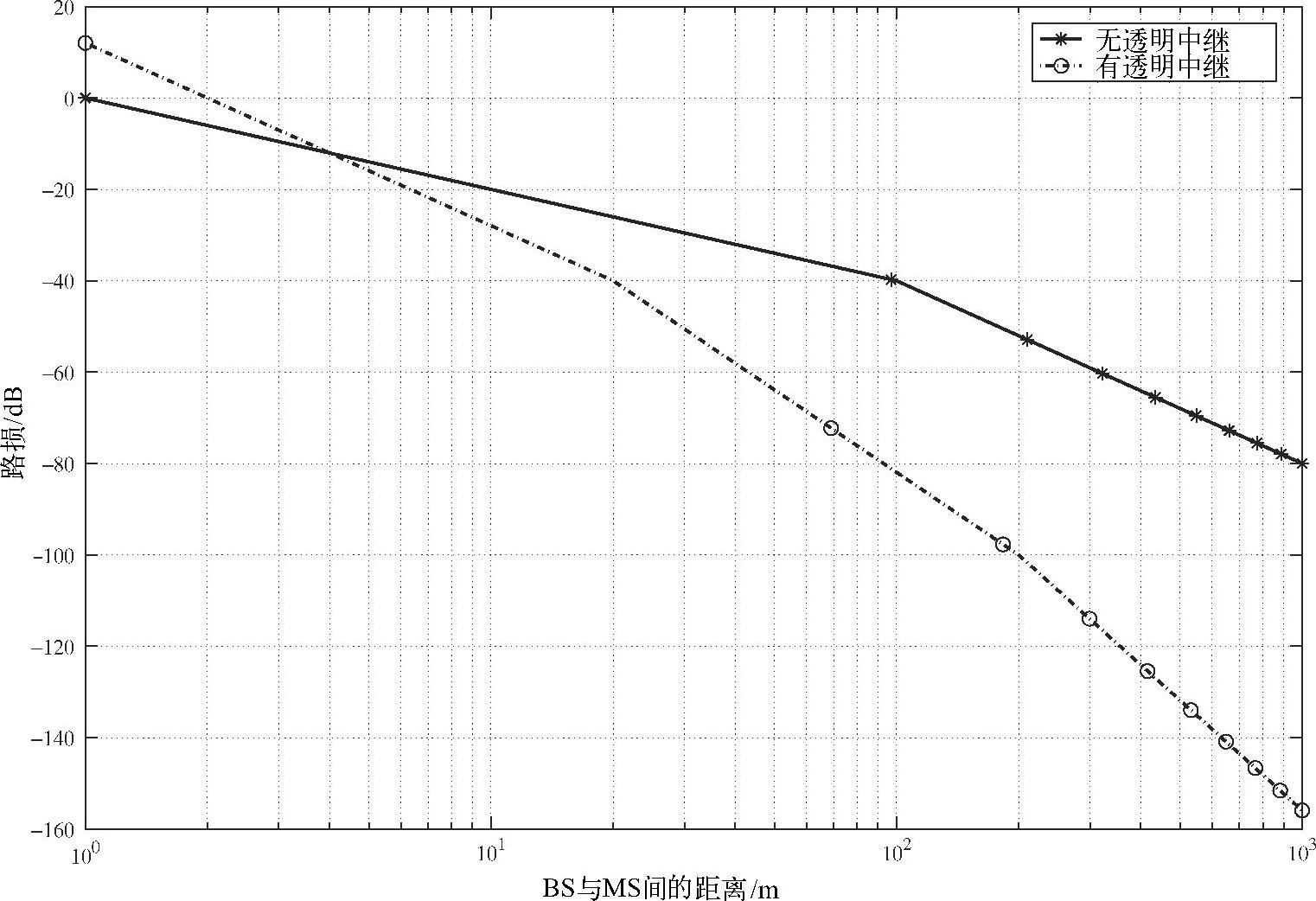
图2.30 假定增益固定，BS和MS之间为中继和非中继链路时，系统的路损和转效点特性

（2）路损的增加

从图2.30中可以看到，在非协同情况下路损是增加的，这可由式（2.15）来解释原因。为了简化计算过程，我们对不同的中继情况都采用了文献[157]中介绍的固定放大系数的单斜率路损模型其形式为

L_i（d）=b_i+n_ilg（d）

其中，b_i为归一化常数；n_i为路损系数。

以dB为单位的端到端路损可以表示为每一级中继信道路损的累加，如：b₁+b₂+n₁lg（d₁）+n₂lg（d₂），其中d=d₁+d₂。假设在发送端和接收端间的中间点采用了透明中继，而且两边的中继段有相同的路损特性，以上的表达式可以简化为2b+2nlg（d/2）。因此端到端的路损参数将调整为

L（d）=b′+n′lg（d） （2.118）

这里取b′=2b-2nlg2，n′=2n。由此可以得出图2.30显示的路损斜率的增加值和截距的偏移值。为了量化任意级数中继情况下的路损，我们假设通信系统源和目的节点之间的距离d=500m，中继在源和目的节点间等距离放置，因此可以产生N个中继段的情况。根据文献[157]的模型，系统的b=-62.01dB，n=5.86，从而得到

b′=-62.01N-5.86lgNdB，n=5.86N。

表2.4总结了非中继情况下，非线性路损特性带来的功率损耗。这些功率损耗对比系统增益来说还是比较大的，但当放大因子变化时损耗会有所减小。

表2.4 当信源和信宿间距500m时，非线性传播模型中的绝对和相对路损

路损对于链路研究具有重大意义，并且路损一般会远超于文献[263]中给出的可能的信噪比增益总和。因此虽然使用透明中继能够降低系统的复杂度，但在系统设计中并不推荐优先使用。

2.4.1.2 阴影

在论及透明中继信道时，需要注意以下三个阴影效应的相关变化：(www.xing528.com)

（1）阴影效应标准偏差的变化

协同通信终端间距的减少会导致阴影效应标准偏差的降低。这一效应已在文献[157]中有量化表达。

（2）阴影方差的增加

在每个中继段阴影信道相互独立的透明中继系统中，阴影效应总量仍然遵循以dB表示的高斯分布，但是直接链路的阴影标准方差一直存在变化。应用式（2.15），可以将固定放大系数下的N级透明中继的有效端到端阴影标准方差表示为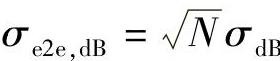。当采用文献[157]所述的更复杂的模型时，N个等间距长中继段的端到端阴影标准方差总和可以这样表示（以dB表示）：

式中，S_s、d₀和D_s为模型特定参量；d是源节点和目的节点之间的距离。假定d=500m，S_s=22.1dB，d₀=10m，D_s=53m，可以根据表2.5查到阴影标准方差的增加。阴影效应的存在是不容忽视的，并且会加剧路损带来的衰减。在表2.5中可以发现，在5个中继段之后阴影损耗开始减少，在20个中继段之后阴影损耗竟然成为了系统增益（表中未显示），这是因为过短距离下会导致阴影标准方差的快速变小。

表2.5 信源和信宿间距500m时，阴影标准方差的非线性特性导致绝对和相对阴影损耗和的变化

（3）阴影相关模型的变化

为了区别于蜂窝模型，文献[169]将协同通信系统下的阴影波动的相关函数标识为联合相关函数（Joint Correlation Function，JCF）。在透明中继系统下还没有可以应用的JCF模型，但根据文献[169]和一些同类文献可以推导出这种模型。这些文献给出透明中继信道的时间自相关函数为

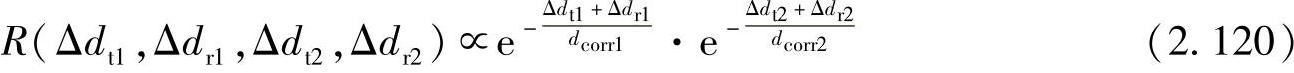
其中、Δd_t1、Δd_r2和Δd_r1=Δd_t2是源、目的和中继节点之间的相对距离；d_corr1和d_corr2是第一个和第二个中继段的空间自相关距离。要注意的是，以上表达式是基于中继自相关间距较小的情况。

总而言之，透明协同中继将会引起严重的阴影衰落，从而降低了阴影相关距离。

2.4.1.3 衰落

为了描述透明中继信道的小尺度衰落特性，我们将会再次讨论通用场景下的几何布置问题，如图2.31所示。假设系统为协同通信系统，系统中存在发送端、中继站、目标移动终端，并以固定速度和固定角度移动。每个终端都装备有多天线，按照三维辐射模型工作，并且在放置时遵循一定的几何规则。同时假定系统覆盖环境是三维并且各向异性的，信道在时间、频率和空间域呈现选择性。研究此模型依然从式（2.6）描述的端到端衰落信道的冲激响应入手，该式为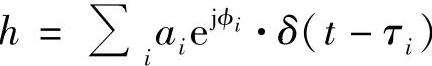，这里a_i、ϕ_i和τ_i通常是相互影响的，并且受潜在的系统假设条件的影响。

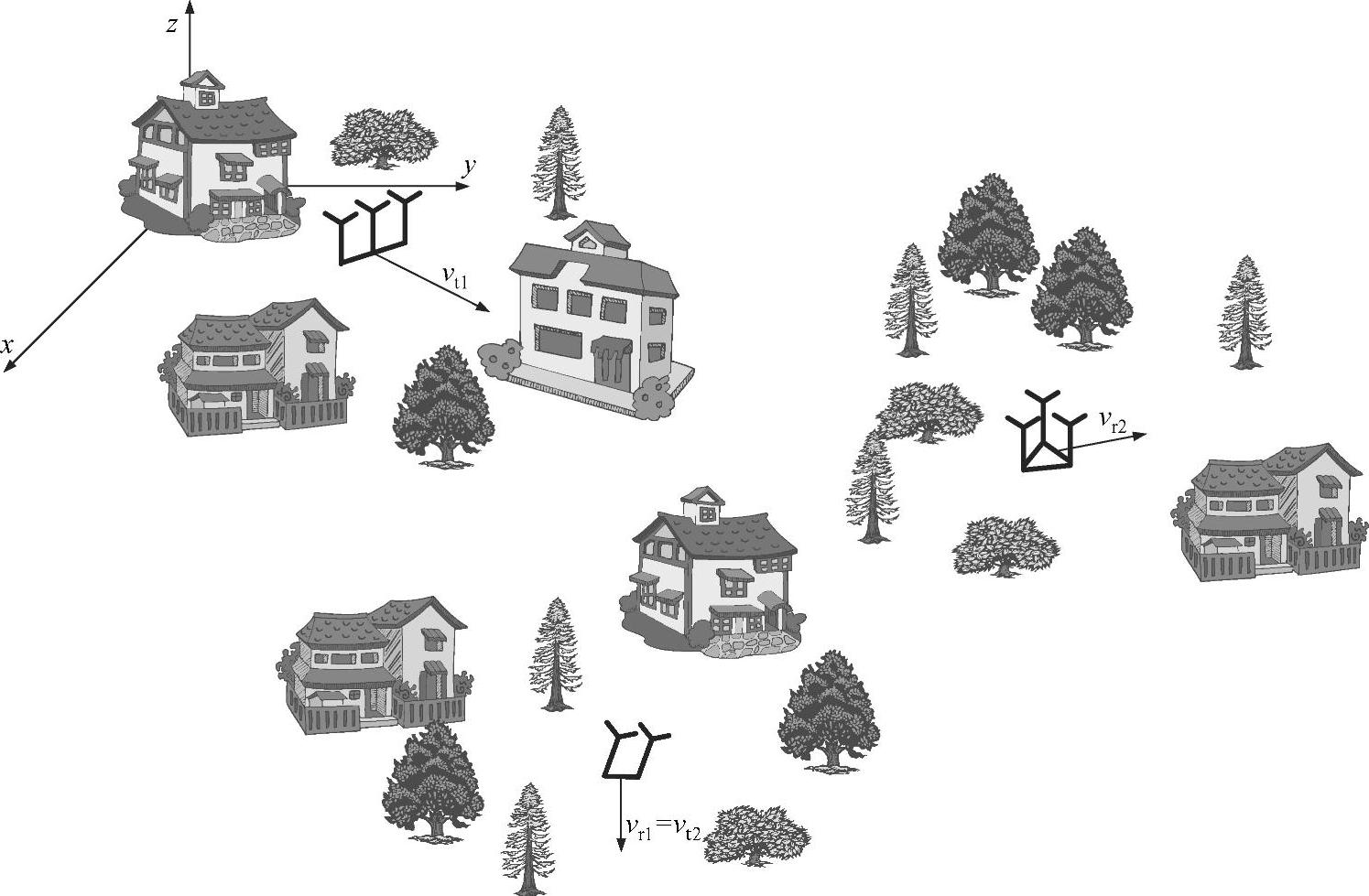
图2.31 透明中继信道的几何布置范例

●幅度/功率统计特性的变化。不同中继段间的耦合会造成信道复杂化，从而导致包络和功率数值大幅改变。

●相关函数的变化。时域、空间域和频域特性也会随着接收端、中继和发送端的移动以及所处环境的杂散程度而改变。

后续章节将要介绍随机信道冲激响应相关的统计和阶矩特性，首先在2.4.2节对端到端窄带系统的参数进行统计分析，然后在2.4.3、2.4.4节中量化分析二阶时域、空间域和频域特性。