现在我们将空、时特性的研究延伸到频域，在频域中，可以假定发射机和接收机都配有多根天线，并且信号分量在时间上可以分解。我们将先从系统假设入手，以获得典型配置场景下的重要结论。最后我们会把研究从典型场景延伸到其他场景。
2.3.5.1 系统假设
最近，一些文献专注于研究宽带MIMO的MS-MS的场景，该场景下，发射机配有Lt根发射天线，接收机配有Lr根发射天线，信号经过频率选择性宽带信道。通过研究这种场景，可以获得信道的瞬时、空间和频域特性。
在早期的文献[199]中讨论了MS-MS的再生SISO宽带信道，并运用射线跟踪法获得车辆间通信系统的功率延迟分布（PDP）。这种模型方法很完善，文献[200]给出了它对系统性能的影响。文献[183，187，201，202]将此模型扩展到MIMO场景，这是将2.3.4节讨论的模型扩展到频域的重要的一步。这个工作本质上是将先前引入的MIMO窄带、带有视距分量的二维双环散射模型、单次反射和二次反射射线扩展到三维宽带场景。与SISO的场景类似，杂散的场景不是以双环形式分布的，而是以文献[203]中讨论的沿着街道峡谷以确定的形式分布。
因此，我们将重点关注文献[187]获得的结果。这个模型中的一些参数有助于估计不同真实环境中的传播特性。文献[187]中的模型符合2.3.3节和2.3.4节中的假设，同时也符合下面的假设：散射体分布在同轴对称圆柱的三维空间内，这使得城市环境中的功率时延谱（PDP）模型更精确。
图2.29给出了这种场景的描述。我们考虑nt×nr的天线配置，其中发射天线和接收天线都配备的是全向天线。发射端和接收端天线元之间的距离分别标记为Δdt和Δdr。发射天线阵列高度为ht，接收天线阵元高度为hr。
图2.29 MIMO宽带再生中继信道的双回波双柱模型
注：对于单次反射分量和视距分量这里不给出描述，但是其原理与二次反射的原理相同
其余符号的定义与窄带SISO和窄带MIMO场景中的符号一致。我们建立原点在发射机的三维坐标系。发射机以速度vt朝着水平角度γt方向移动。接收机在x-y平面面内以速度vr朝着角度γr方向移动。θt和θr分别是x-y平面面内发射天线阵列和接收天线阵列的水平方向角。ψt和ψr分别是y-z面内发射天线阵列和接收天线阵列的垂直方向角。
发射机周围的M个全向散射体散布在半径为Rt1和Rt2的圆柱之间的空间，因此可以看做是分布在半径为Rt（l）的L个圆柱体表面，每个圆柱l表面包含M（l）个散射体，标记为St（m，l），其中Rt1≤Rt（l）≤Rt2，1≤l≤L，1≤m≤M（l）。类似地，接收机周围的N个全向散射体占据着半径为Rr1和Rr2的圆柱之间的空间，这N个散射体分布在半径为Rr（k）的P个圆柱体表面，因此每个圆柱k表面包含N（k）个散射体，标记为St（n，k），其中Rr1≤Rr（k）≤Rr2，1≤k＜p，1≤n≤N（k）。
从发射天线p发射的波与发射机周围的第l个圆柱表面的第m个散射体碰撞，产生的水平出射角（AAOD）为αt（m，l）、垂直出射角（EAOD）为βt（m，l）的。类似地，从发射天线p发射的波与接收机周围的第k个圆柱表面的第n个散射体碰撞，产生的水平到达角（AAOA）为αt（n，k），垂直到达角（EAOA）为βt（n，k）。LOS分量的水平到达角（AAOA）记做αRLOqS。
发射机和接收机间的距离为D。第p根发射天线和发射机周围的第l个圆柱表面的第m个散射体之间的距离记为dp，m，l，发射机周围的第l个圆柱表面的第m个散射体和第q个接收天线之间的距离记为dm，l，q，第p根发射天线和接收机周围的第k个圆柱表面的第n个散射体之间的距离记为dp，n，k，接收机周围的第k个圆柱表面的第n个散射体和第q个接收天线之间的距离记为dn，k，q，发射机周围的第l个圆柱表面的第m个散射体和接收机周围的第k个圆柱表面的第n个散射体之间的距离记为dm，l，n，k，第p根发射天线和第q个接收天线之间的距离记为dp，q。
基带宽带信道可以看做是LOS分量、在发射机反射（SBT）和在接收机反射（SBR）的单回波分量和双回波分量的叠加。对于第p根发射天线和第q个接收天线之间的信道，有[187]：
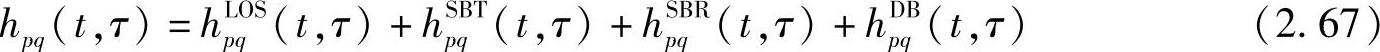
为了简化过程，文献[187]使用了时变频率传递函数而不是式（2.67）的时延扩展函数，前者是后者关于延迟的傅里叶变换。因此有
其中，各个分量分别为
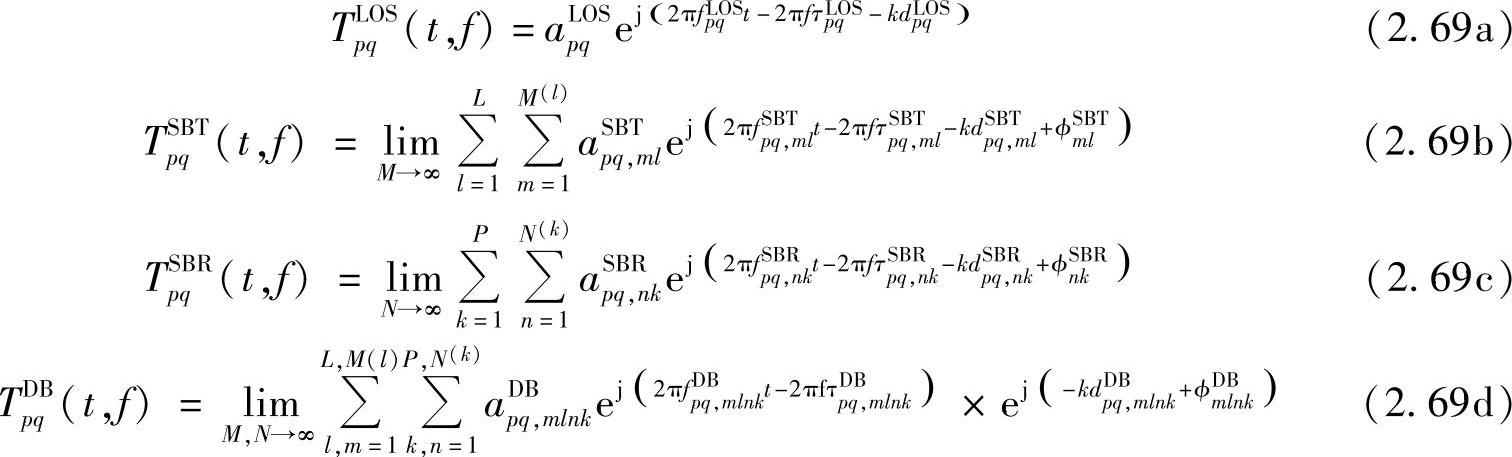
式中，忽略上标和下标，a和ϕ分别是由波和散射体相互作用而产生的信道增益和相位偏移；f是由发射机和接收机移动而产生的多普勒频移；τ是由三维散射体导致的信道多径分量（MPC）的延迟；kd是由波从发射机到接收机传输了距离dF0的相位偏移。这些变量可以按照以下公式计算得到：
（1）幅度
幅度参照2.3.3节和2.3.4节给出的推导。另外，分配给发射天线p和接收天线q之间的视距分量的功率为Kpq/（1+Kpq），分配给非视距分量部分的功率为1/（1+Kpq）。因为max（Δdt，Δdr）＜＜min（Rt，Rr），我们可以假设所有天线的莱斯衰落因子都相同，即对所有的1≤p≤Lt和1≤q≤Lr，都有Kpq=K。我们可以假设分配给SBT、SBR和DB分量的相对功率分别是ηt、ηr和ηtr，并且ηt+ηr+ηtr=1。也可以假设发射天线p到接收天线q的信道功率记为Ωpq。这些参数或者在仿真时设定或者根据测量来确定。我们可以通过下面的公式计算：
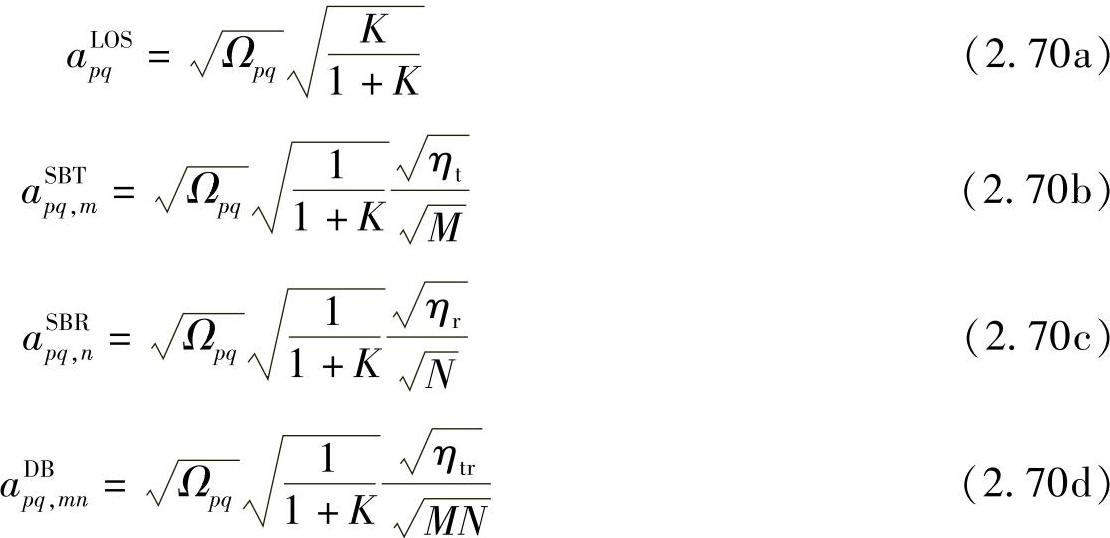
功率Ωpq由Ωpq=PpqD-n（λ/4π）2给出，其中Ppq是从发射天线p到接收天线q的发射功率，n是路损因子。
（2）相位
按照2.3.3节和2.3.4节的讨论，假设所有的相位ϕ在[0，2π）内都是随机均匀分布的。
（3）多普勒频移
多普勒频移取决于发射机或接收机的移动方向和波出射或到达方向之间的几何关系：
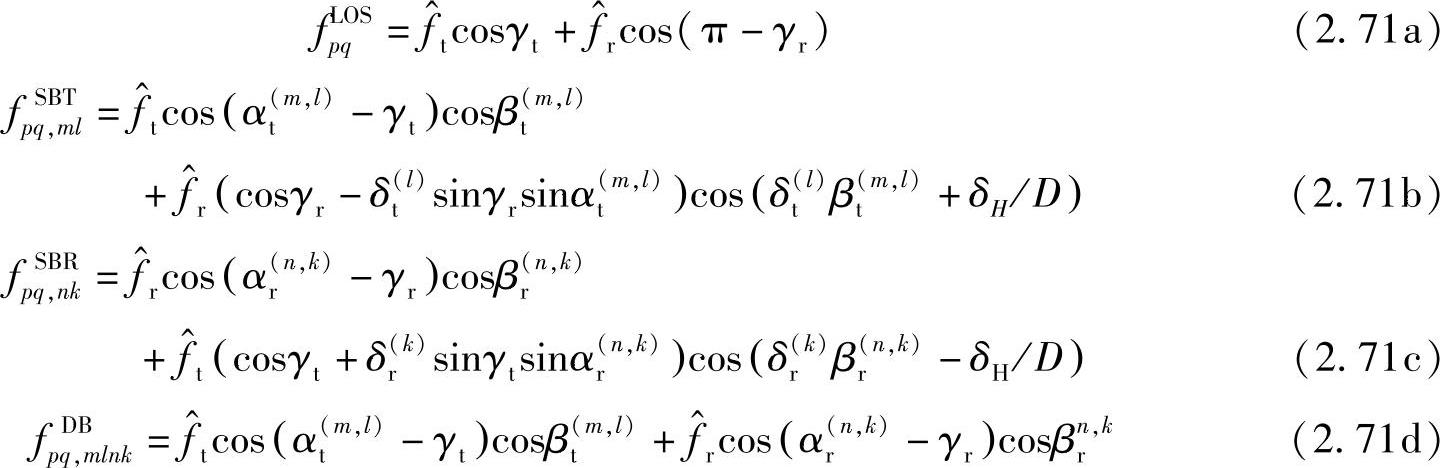
其中，
和f
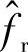分别是发射机和接收机的最大多普勒频移，它们可计算为
和
，fc是载波频率，λ是波长。而且δt（l）=Rt（l）/D，δr（k）=Rr（k）/D，δH=ht-hr。注意，与SISO的场景类似，因为任意一端的散射体的数量趋近于无穷大，所以这些离散的随机角度的概率密度函数都是连续的。
（4）路径长度
如图2.29所示，波的路径长度可以由下式表示：
下面分两种情况讨论，即D明显大于max（Rt，Rr）和D与max（Rt，Rr）相近时的情况。后者主要发生在室内并要求精确表示所用的距离，其闭式表达式可参考文献[173]。对于D＜＜max（Rt，Rr）的情况，可以对单个路径长度运用下面的简化表达式计算[187]：
其中，δt，x=Δdtcosψtcosθt，δt，y=Δdtcosψtsinθt，δt，z=Δdtsinψt，δr，x=Δdrcosψrcosθr，δr，y=Δdrcosψrsinθr，δr，z=Δdrsinψr。
（5）信道多径分量（MPC）的延迟
MPC的延迟可以从往返距离推算出来，并且可以由下式表示：
其中，c是光速。
现在我们可以来推导出MS-MS的MIMO衰落信道相关的时间、空间和频率的关键参数。(www.xing528.com)
2.3.5.2 典型场景
根据文献[187]，空-时-频相关函数（STF-CF）和它的功率谱密度（PSD）可以按照下面的公式计算。
（1）空-时-频相关函数STF-CF
使用上面的变量和式（2.39）中相同的方法，发射-接收天线对pq和其他天线对pq之间的合成衰落信道的STF-CF的计算方法如下：
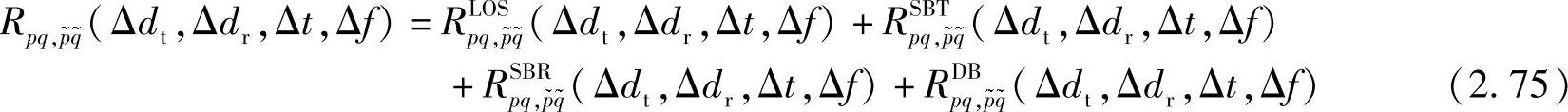
其中，各个相关函数可从文献[187]中获得，并可通过下面的公式计算得到：
其余的变量由以下公式表示：
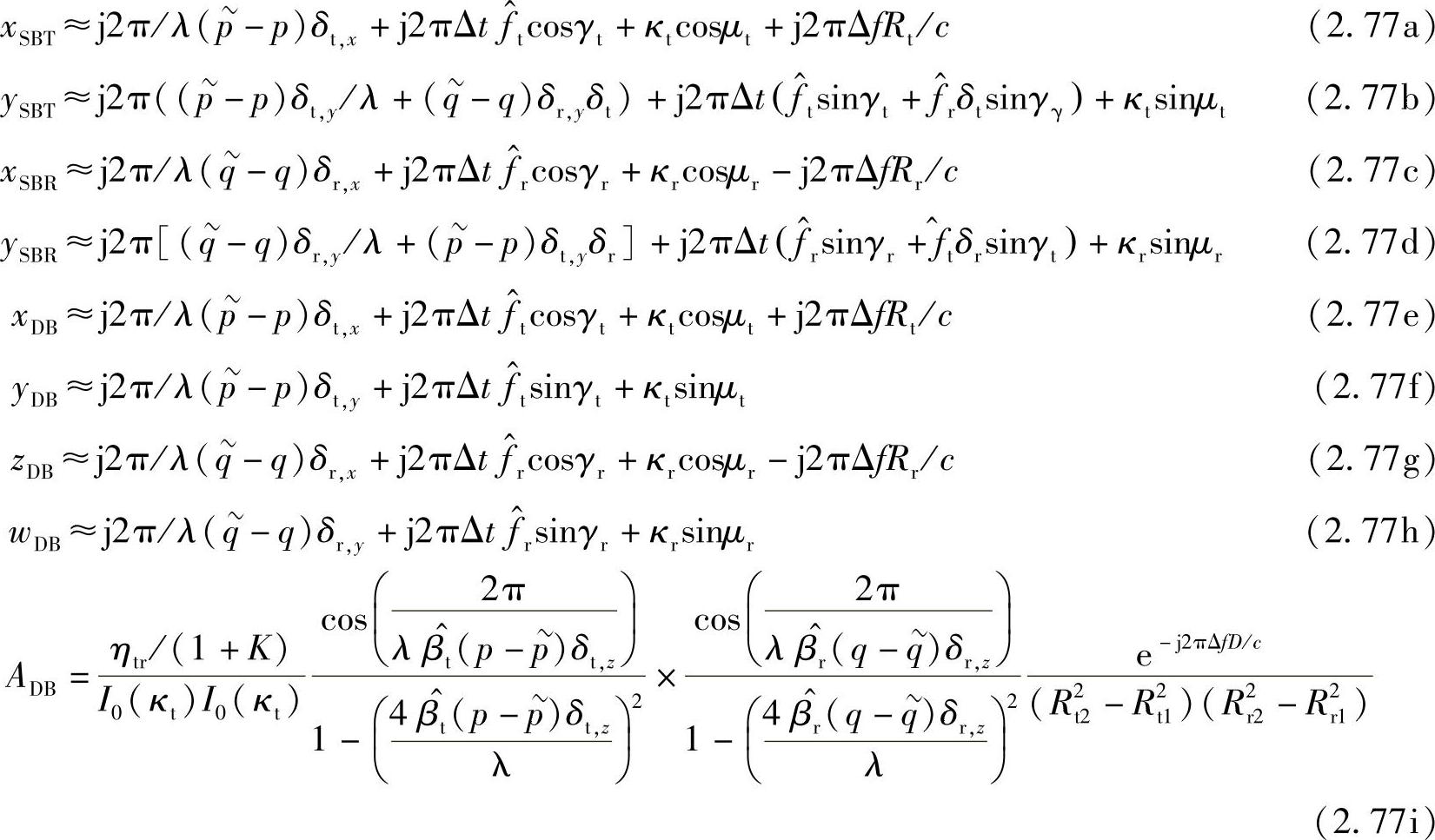
对于发送端和接收端圆柱散射环的半径Rt（l）和Rr（k）的，我们可以假定为均匀分布。例如，发射端
对于AAOD和AAOA的角度分布，我们可以假定发送端和接收端分别服从均值参数μt、参数κt和均值μr、参数κr的vonMises分布，式（2.44）已经给出了这种分布。对于EAOD和EAOA的垂直分布，可以使用均匀分布、余弦分布和高斯分布来表示；在这里我们使用如下分布，这种分布典型地用在由街道主导的城市环境中[187，204，205]：
其中，
是最大垂直角，范围为
；发射天线阵列和接收天线阵列的最大垂直角分别记为
和
。
（2）多普勒功率谱
多普勒功率谱可由上述的STF-CF对于时间间隔Δt在Δf=0的傅里叶变换得到，本质上会产生空间多普勒功率谱密度。运用式（2.40）～（2.75）中的变换关系可以生成下面的式子[187]：
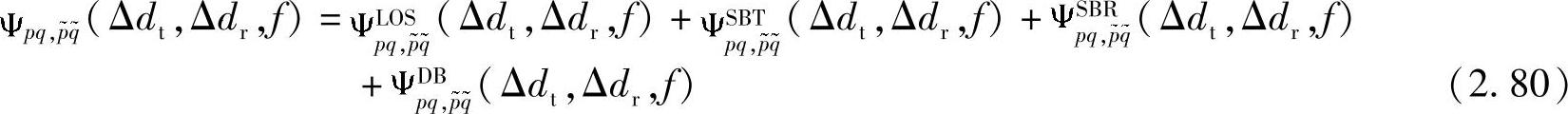
其中各个功率谱密度如下[187]：
其中，*代表了频率f的卷积。其他变量的表示如下：
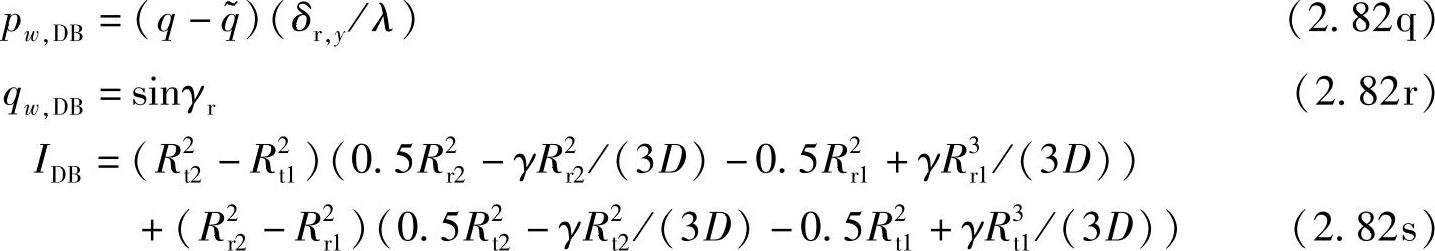
要注意的是，本书并未给出二次反射形式卷积的精确表达式。但是，包含该形式的任何数值计算方法都是相当简单的。
（3）电平交叉率（LCR）
信道包络的电平交叉率可以根据文献[186]中的一些思路计算得到，但只限于存在LOS分量的情况。最终的表达式如下[202]：
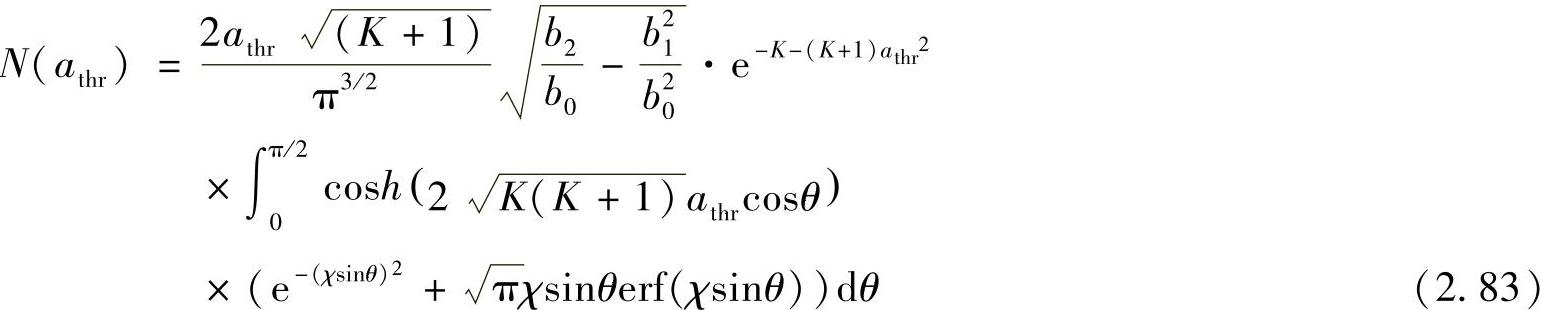
其中，
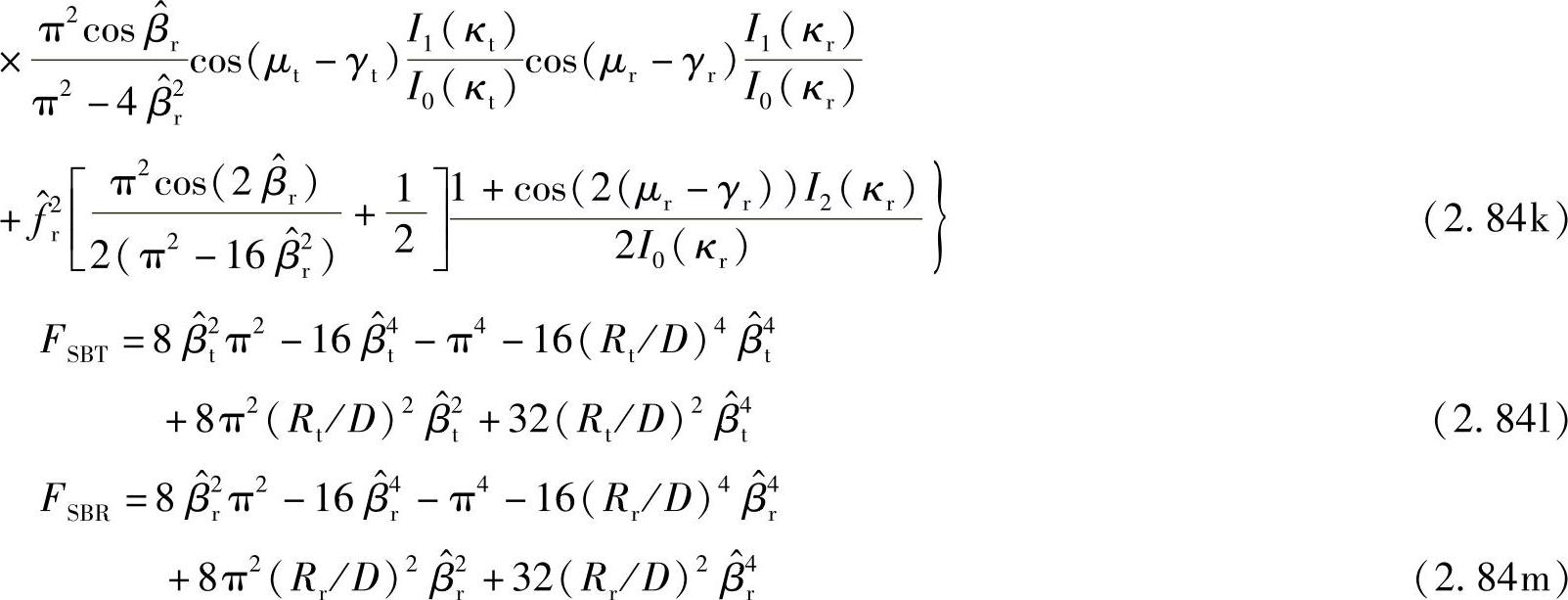
其中，积分需要进行数值估计。
（4）平均衰落时长
因为信道包络是莱斯分布，平均衰落时长由下式给出：
其中，Q（·，·）是Marcum Q函数。
根据上面的通用表达式，现在我们可以研究一些参数的相关函数和它的频谱密度的特性。
2.3.5.3 场景分析
在文献[202]中已经详细讨论和分析了一系列的参数，并将上面的公式简化为适用于典型配置，如窄带场景、Jakes场景等；该研究同时表明，该模型也适用于亚特兰大和乔治亚的宽带测量。因此，我们将在此省略对场景的具体研究。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
