滚动轴承性能测试分析实验探究

【实验目的】

（1）了解和掌握滚动轴承径向载荷分布及变化实验，测试在总径向载荷和轴向载荷作用下，滚动轴承径向载荷分布及变化情况，特别是轴向载荷对滚动轴承径向载荷分布的影响，并作出载荷分布曲线；

（2）了解和掌握滚动轴承元件上载荷动态分析实验，测试滚动轴承元件上的载荷随时间的变化情况，并作出变化曲线；

（3）了解和掌握滚动轴承组合设计实验，测试滚动轴承组内部轴向载荷、径向载荷和总轴向载荷的关系，并进行滚动轴承组合设计计算。

【实验仪器与设备】

1.实验台系统框图

实验台系统框图如图3.3.1所示。

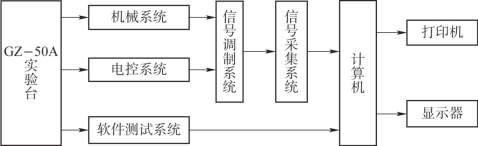
图3.3.1　实验台系统框图

2.实验台机械结构

实验台机械结构如图3.3.2所示。

图3.3.2　试验台机械结构

1—电动机；2—限位顶杆；3—左支座；4—左、右传感器座；5—径向加载装置；6—主轴；7—导杆；8—右支座；9—轴向加载装置；10—左、右轴向载荷装置；11—机座；12—联轴器。

3.实验台工作过程

起动电动机l（静态测试时不起动电机），径向加载装置5调节至设定作用点且逐步加载，左、右传感器座4中的滚动轴承处于工作状态。施加于主轴6上的径向载荷传输至滚动轴承的滚动体，滚动体所受之力，通过传感活塞传输给传感器座4中的径向载荷传感器，经控制器到计算机，通过计算机显示器显示各种受力状态的技术性能数据、曲线和图表；同时，左、右轴向载荷传感器10测量出由径向载荷产生的内部轴向载荷技术参数。移动径向加载装置5，改变径向载荷作用点，左、右传感器座4中的滚动轴承受力状态将随之改变，由此可测试出各种不同工况下的技术参数、曲线和图表。

当轴向加载装置9加载时，左传感器座4中的径向载荷传感器测量出由轴向加载时产生的径向分力信号，左、右轴向载荷传感器10测量出滚动轴承所受轴向载荷和总轴向载荷的技术数据。

根据所测各种技术参数、曲线和图形，可分析出滚动轴承最佳受力状态，从而设计出滚动轴承最佳受力工况和结构。

【实验原理】

1.滚动轴承径向载荷分布

左、右滚动轴承各装有8个径向载荷传感器，可通过计算机测绘滚动轴承在轴向、径向载荷作用下轴承径向载荷分布变化情况。

1）深沟球轴承（向心轴承）载荷分布曲线

以向心轴承为例。轴承工作的某一瞬间，滚动体处于图3.3.3所示的位置，径向载荷Fr通过轴径作用于内圈，位于上半圈的滚动体不会受力，而由下半圈的滚动体将此载荷传到外圈上。如果假定内、外圈的几何形状并不改变，则由于它们与滚动体接触处共同产生局部接触变形，内圈将下沉一个距离。设在载荷Fr作用线上的接触变形量为δ0，按变形协调关系，不在载荷Fr作用线上其他各点的径向变形量为：δi=δ0 cos（iγ），i=1，2，…，L。也就是说，真实的变形量的分布是中间最大，向两边逐渐减小。可以进一步判断，接触载荷也是处于Fr作用线上的接触点处最大，向两边逐渐减小。各滚动体从开始受力到受力终止所对应的区域叫作承载区。

根据力的平衡原理，所有滚动体作用在内圈上的反力FNi的合力必定等于径向载荷Fr。

实际上由于轴承内存在游隙，故由径向载荷Fr产生的承载范围将小于180°。也就是说，不是下半部滚动体全部受载。这时，如果同时作用有一定的轴向载荷，可以使承载区扩大。

图3.3.3　滚动轴承受力分析

2）轴向载荷对载荷分布的影响

角接触球轴承或圆锥滚子轴承（现以圆锥滚子轴承为例）承受径向载荷Fr时，由于滚动体与滚道的接触线与轴承轴线之间夹一个接触角，因而各滚动体的反力并不指向半径方向，它可以分解为一个径向分力和一个轴向分力，如图3.3.4所示。用来代表某一个滚动体反力的径向分力为FNi，如图3.3.4（b）所示，则相应的轴向分力应等于Fdi。所有径向分力FNi的合力与径向载荷Fr相平衡；所有的轴向分力Fdi之和组成轴承的内部轴向力（派生轴向力）Fd，它迫使轴颈（连同轴承内圈和滚动体）有向右移动的趋势，这应由轴向力Fa来与之平衡，如图3.3.4（a）所示。

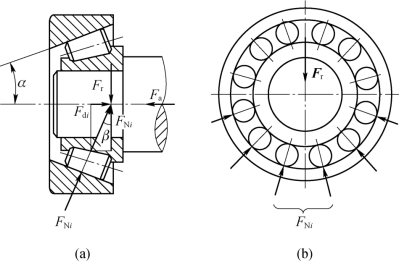
图3.3.4　圆锥滚子轴承的受力

（a）径向分力和轴向分力；（b）径向载荷平衡

当只有最下面一个滚动体受载时，有

受载的滚动体数目增多时，如图3.3.5所示，虽然在同样的径向载荷Fr的作用下，但内部轴向力（派生的轴向力）Fd将增大，即

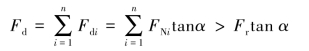
式中：n为受载的滚动体数目；Fdi是作用于各滚动体上的派生的轴向力；FNi是作用于各滚动体上的径向分力；尾部的不等式也表明了n个FNi的代数和大于它们的向量和。这时，平衡内部轴向力（派生轴向力）Fd所需施加的轴向力Fa为

2.滚动轴承元件上载荷动态分析

通过计算机直接测量滚子对外圈的压力及变化情况，绘制滚动体内、外圈载荷变化曲线。

轴承工作时，各个元件上所受的载荷及产生的应力是随时间变化的。根据上面的分析，当滚动体进入承载区后，所受载荷即由0逐渐增加到FN2、FN1直到最大值FN0，然后再逐渐降低至FN1，FN2直至0。就滚动体上某一点而言，它的载荷及应力是周期性地不稳定变化的，如图3.3.6（a）所示。

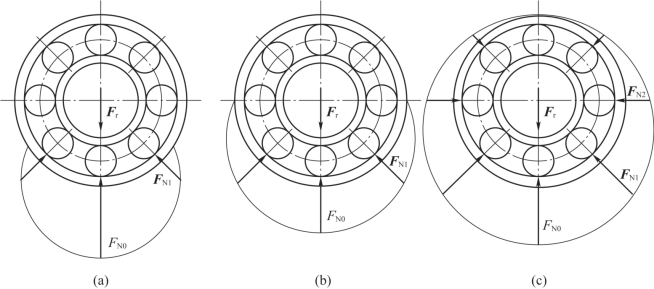
图3.3.5　轴承中受载滚动体数目的变化

滚动轴承工作时，可以是外圈固定、内圈转动，也可以是内圈固定、外圈转动。对于固定套圈，处在承载区内的各接触点，按其所在位置的不同，将受到不同的载荷。处于Fr作用线上的点将受到最大的接触载荷。对于每一个具体的点，每当一个滚动体滚过时，便承受一次载荷，其大小是不变的，也就是承受稳定的脉动循环载荷的作用，如图3.3.6（b）所示。载荷变动的频率快慢取决于滚动体中心的圆周速度，当内圈固定外圈转动时，滚动体中心的运动速度较大，故作用在固定套圈上的载荷的变化频率也较高。

转动套圈上各点的受载情况，类似于滚动体的受载情况，可用图3.3.6（a）所示的曲线描述。

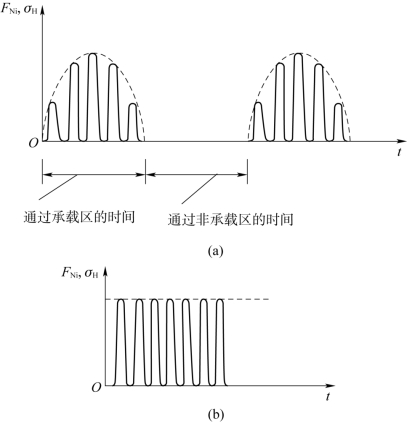
图3.3.6　滚动轴承元件上载荷

（a）滚动体上某一点的载荷；（b）固定套圈上某一点的载荷

3.滚动轴承组合设计计算

左、右滚动轴承座可轴向移动，均装有轴向载荷传感器，可通过计算机测试并计算单个滚动轴承轴向载荷与总轴向载荷的关系，从而进行滚动轴承组合设计计算。

1）滚动轴承的当量动载荷

滚动轴承的基本额定动载荷是在一定的运转条件下确定的，如载荷条件为：向心轴承仅承受纯径向载荷Fr，推力轴承仅承受纯轴向载荷Fa。实际上，轴承在许多应用场合，常常同时承受径向载荷Fr和轴向载荷Fa。因此，在进行轴承寿命计算时，必须把实际载荷转换为确定基本额定动载荷的载荷条件相一致的当量动载荷，用P表示。这个当量动载荷，对于以承受径向载荷为主的轴承，称为径向当量动载荷，用Pr表示；对于以承受轴向载荷为主的轴承，称为轴向当量动载荷，用Pa表示。当量动载荷P（Pr或Pa）的一般计算公式为(www.xing528.com)

式中：X、Y分别为径向动载荷系数和轴向动载荷系数。

对于只能承受纯径向载荷Fr的轴承，有

对于只能承受纯轴向载荷Fa的轴承，有

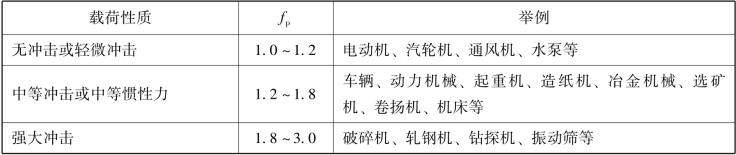
按以上三式求得的当量动载荷仅为一理论值。实际上，在许多支承中还会出现一些附加载荷，如冲击力、不平衡作用力、惯性力以及轴挠曲或轴承座变形产生的附加力等，这些因素很难在理论上精确计算。为了考虑到这些影响，可对当量动载荷乘上一个根据经验而定的载荷系数fp，其值参见表3.3.1。故实际计算时，轴承的当量动载荷

表3.3.1　载荷系数fp

2）角接触球轴承和圆锥滚子轴承的径向载荷Fr与轴向载荷Fa的计算

角接触球轴承和圆锥滚子轴承受径向载荷时，要产生内部轴向力（派生的轴向力），为了保证这类轴承正常工作，通常将其成对使用，如图3.3.7所示。

图3.3.7　角接触球轴承和圆锥滚子轴承轴向的分析

（a）反装；（b）正装

在计算各轴承的当量动载荷P时，其中的径向载荷Fr即为由外界作用到轴上的径向力Fre在各轴承上产生的径向载荷；但其中的轴向载荷Fa并不完全由外界的轴向作用力Fae产生，而是应该根据整个轴上的轴向载荷（包括因径向载荷Fr产生的派生轴向力Fd）之间的平衡条件得出。

根据力的径向平衡条件，很容易由外界作用到轴上的径向力Fre计算出两个轴承上的径向载荷Fr1、Fr2，当Fre的大小及作用位置固定时，径向载荷Fr1、Fr2也就确定了。由Fr1、Fr2派生的轴向力Fd1、Fd2的大小可按照表3.3.2中的公式计算。计算所得的Fd值，相当于正常的安装情况，即大致相当于有半数滚动体全部受载时的派生轴向力（轴承实际的工作情况不允许比这样更坏）。

表3.3.2　约有半数滚动体接触时派生轴向力Fd的计算公式

如图3.3.7所示，把派生轴向力的方向与外加轴向载荷Fae的方向一致的轴承标为2，另一端标为轴承1。取轴和与其相配合的轴承内圈为分离体，如达到轴向平衡时，应满足

如果按表3.3.2中的公式求得的Fd1和Fd2不满足上面的关系式时，出现以下2种情况。

（1）当Fae+Fd2＞Fd1时，则轴有向左窜动的趋势，相当于轴承1被“压紧”，轴承2被“放松”。但实际上轴必须处于平衡位置（即轴承座必然要通过轴承元件施加一个附加的轴向力来阻止轴的窜动），所以被“压紧”的轴承1所受的总轴向力Fa1必须与Fae+Fd2相平衡，即

而被“放松”的轴承2只受其派生的轴向力Fd2，即

（2）当Fae+Fd2＜Fd1时，同前，被“放松”的轴承1只受其本身派生的轴向力Fd1，即

而被“压紧”的轴承2所受的总轴向力为

综上可知，计算角接触球轴承和圆锥滚子轴承所受轴向力的方法可以归结为：先通过派生轴向力及外加轴向载荷的计算与分析，判定被“放松”或被“压紧”的轴承；然后确定被“放松”轴承的轴向力仅为其本身派生的轴向力，被“压紧”轴承的轴向力则为除去本身派生的轴向力后其余各轴向力的代数和。

轴承反力的径向分力在轴心线上的作用点叫轴承的压力中心。图3.3.7所示的2种安装方式，对应2种不同的压力中心的位置。当两轴承支点间的距离不是很近时，常以轴承宽度中点作为支点反力的作用位置，这样计算起来比较方便，且误差也不大。

【实验方法和步骤】

（1）实验之前，细读使用说明书，检查径向分布传感器紧定螺栓是否松动；专用内六角扳手拧紧，以不松动为宜。

（2）检查电源插头、信号电缆插头是否牢固。按下控制面板上“电源”按钮，检查电压表是否有电显示；按下“信号”按钮计算机显示器中才能有传感信号数据显示。

（3）打开计算机，按照软件程序要求操作。将每路传感器施加适当的预紧力，确保各传感器受载状态正常。每做一项实验之前，必须“空载调零”；做完一项实验之后，必须及时卸载，避免传感器长时间受载而影响性能和使用寿命。

（4）测试静载荷径向分布模块时，轴承滚珠之一必须对准下方的准线，才能测试出正确的分布规律和分布曲线。计算机中显示的数据不正确，即是未对准，按“点动”按钮或用手辅助旋转主轴重新操作至对准为止。

（5）打开实验软件主界面，如图3.3.8所示。单击空载调零选定测试对象，将径向加载装置调至设定位置，并逐渐加载。测试静态加载时，总径向载荷最大加至1 000（10 N）。

图3.3.8　实验软件界面

（6）单击“径向分布”再单击“无轴向载荷径向分布”，然后加轴向载荷，一般设置为500（10 N）左右，最后单击“有轴向载荷径向分布”，如图3.3.9所示。

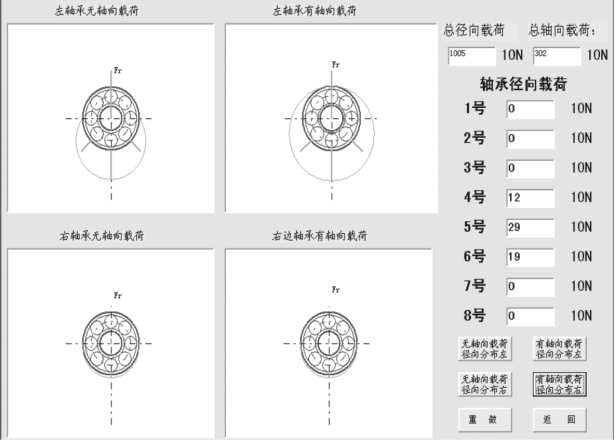
图3.3.9　载荷设置

（7）测试动载荷动态曲线.起动电动机，将径载装置调至设定位置，逐渐加载至500（10 N）左右为宜，且不能同时施加轴向载荷。单击“外圈载荷变化曲线”，当出现动载荷最大值时，再单击“滚动体载荷变化曲线”，如图3.3.10所示。

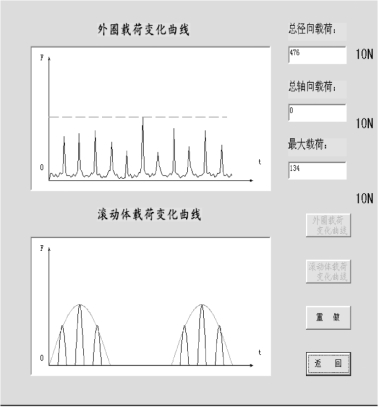
图3.3.10　外圈载荷变化曲线

（8）测试轴承组合设计计算模块时，总径向载荷加至500（10 N）左右为宜，且不要对准底部准线；在施加总轴向载荷之前，先要空载保存由总径向载荷派生的内部轴向载荷数据；总轴向载荷加至400（10 N）左右为宜，且不能作动态运行。

（9）单击“理论计算”进入滚动轴承设计计算界面，将径向加载装置调至设定位置，逐渐加载。单击“结果保存”再施加轴向载荷，单击“实测计算”，同时单击“理论计算”进行对比分析，如图3.3.11所示。

图3.3.11　滚动轴承计算界面

（10）实验结束，退出软件界面，关机。