薄壁圆筒弯扭组合变形主应力测定

【实验目的】

（1）用电测法测定平面应力状态下主应力的大小及方向，并与理论值进行比较；

（2）测定薄壁圆筒在弯扭组合变形作用下的弯矩和扭矩；

（3）进一步掌握电测法。

【实验仪器设备和工具】

（1）弯扭组合实验装置；

（2）力和应变综合参数测试仪；

（3）游标卡尺、钢板尺。

【实验原理和方法】

1.测定主应力大小和方向

薄壁圆筒受弯扭组合作用，发生组合变形。圆筒的m点处于平面应力状态，如图1.6.1所示。在m点单元体上作用有由弯矩引起的正应力σx，由扭矩引起的剪应力τn，主应力是一对拉应力σ1和一对压应力σ3。单元体上的正应力σx和剪应力τn的计算式分别为

式中：M——弯矩，M=PL；

　　　Mn——扭矩，Mn=Pa；

　　　Wz——抗弯截面模量，对空心圆筒有

　　　WT——抗扭截面模量，对空心圆筒有

图1.6.1　圆筒m点应力状态

由二向应力状态分析可得到主应力及其方向为

本实验装置采用的是45°直角应变花，在m、m′点各贴一组应变花，应变花上3个应变片的α角分别为-45°、0°、45°（见图1.6.2），该点主应变和主方向为

主应力和主方向为

图1.6.2　测点应变片布置图

2.测定弯矩

薄壁圆筒虽为弯扭组合变形，但m和m′两点沿x方向只有因弯曲引起的拉伸和压缩应变，且两应变等值异号。因此，将m和m′两点应变片b和b′，采用不同组桥方式测量，即可得到m、m′两点由弯矩引起的轴向应变εM，则截面m-m′的弯矩实验值为

3.测定扭矩

当薄壁圆筒受纯扭转时，m和m′两点45°方向和-45°方向的应变片都是沿主应力方向，且主应力σ1和σ3数值相等符号相反。因此，采用不同的组桥方式测量，可得到m和m′两点由扭矩引起的主应变εn。由扭转时主应力σ1和剪应力τ相等，可得截面m-m′的扭矩实验值为

【实验步骤】

（1）设计好本实验所需的各类数据表格。

（2）测量试件尺寸、加力臂长度和测点距力臂的距离，确定试件有关参数，如表1.6.1所示。

（3）将薄壁圆筒上的应变片按不同测试要求接到仪器上，组成不同的测量电桥。调整好仪器，检查整个测试系统是否处于正常工作状态。

主应力大小、方向测定：将m和m′两点的所有应变片按半桥单臂、公共温度补偿法组成测量线路进行测量。(www.xing528.com)

测定弯矩时，将m和m′两点的b和b′两应变片按半桥双臂组成测量线路进行测量

测定扭矩时，将m和m′两点的a、c和a′、c′四只应变片按全桥方式组成测量线路进行测量

（4）拟定加载方案。先选取适当的初载荷P0（一般取P0=10%Pmax），估算Pmax（该实验载荷范围Pmax≤700 N），分4～6级加载。

（5）根据加载方案，调整好实验加载装置。

（6）加载。均匀缓慢加载至初载荷P0，记下各点应变的初始读数；然后分级等增量加载，每增加一级载荷，依次记录各点电阻应变片的应变值，直到最终载荷。实验至少重复2次。实验数据记录在表1.6.2和表1.6.3中。

（7）做完实验后，卸掉载荷，关闭电源，整理好所用仪器、设备，清理实验现场，实验资料交指导教师检查签字。

（8）实验装置中，圆筒的管壁很薄，为避免损坏，切勿超载，且不能用力扳动圆筒的自由端和力臂。

表1.6.1　试件相关数据

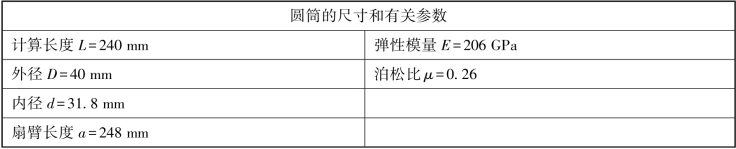
表1.6.2　实验数据

表1.6.3　实验数据

【实验结果处理】

1.主应力及方向

m或m′点实测值主应力及方向的计算式为

m或m′点理论值主应力及方向的计算式为

2.弯矩及扭矩

m-m′实测值弯曲应力及剪应力计算如下：

m-m′理论值弯曲应力及剪应力的计算式为

3.实验值与理论值比较

m或m′点主应力及方向如表1.6.4所示。

表1.6.4　m或m′点主应力及方向

续表

m-m′截面弯矩和扭矩如表1.6.5所示。

表1.6.5　m-m′截面弯矩和扭矩

【思考题】

（1）测量单一内力分量引起的应变，可以采用那几种桥路接线法？

（2）主应力测量中，45°直角应变花是否可沿任意方向粘贴？

（3）对测量结果进行分析讨论，产生误差的主要原因是什么？