【实验目的】
(1)测定常用金属材料的弹性模量E和泊松比μ;
(2)验证胡克定律。
【实验仪器设备和工具】
(1)组合实验台中拉伸装置;
(2)XL2118系列力和应变综合参数测试仪;
(3)游标卡尺、钢板尺。
【实验原理和方法】
试件采用矩形截面试件,电阻应变片布片方式如图1.4.1所示。在试件中央截面上,沿前、后两面的轴线方向分别对称地贴一对轴向应变片R1、R1′和一对横向应变片R2、R2′,以测量轴向应变ε和横向应变ε′。
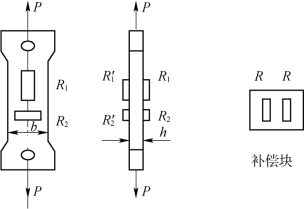
图1.4.1 拉伸试件及布片方式
1.弹性模量E的测定
由于实验装置和安装初始状态的不稳定性,拉伸曲线的初始阶段往往是非线性的。为了尽可能减小测量误差,实验宜从一初载荷P0(P0≠0)开始,采用增量法,分级加载,分别测量在各相同载荷增量ΔP作用下,产生的应变增量Δε,并求出Δε的平均值。设试件初始横截面面积为A0,又因![]() ,则有
,则有
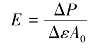
式中:A0——试件截面面积;
Δε——轴向应变增量的平均值。
上式即为弹性模量E的计算公式。
用上述矩形截面试件测E时,合理地选择组桥方式可有效地提高测试灵敏度和实验效率。下面讨论几种常见的组桥方式。
1)单臂测量
如图1.4.2(a)所示,实验时,在一定载荷条件下,分别对前、后两轴向应变片进行单片测量,并取其平均值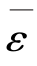 =(ε1-ε1′)/2。显然,(
=(ε1-ε1′)/2。显然,(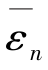 +ε0)代表载荷(
+ε0)代表载荷(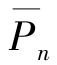 +P0)作用下试件的实际应变量。而且
+P0)作用下试件的实际应变量。而且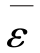 消除了偏心弯曲引起的测量误差。
消除了偏心弯曲引起的测量误差。
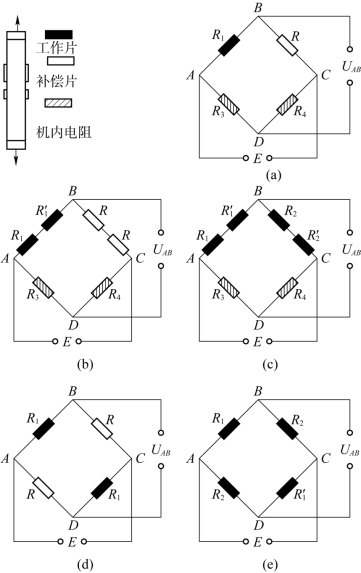
图1.4.2 几种不同的组桥方式
(a)单臂测量;(b)轴向应变片串联后的单臂测量;(c)串联后的半桥测量;(d)相对桥臂测量;(e)全桥测量
2)轴向应变片串联后的单臂测量
如图1.4.2(b)所示,为消除偏心弯曲引起的影响,可将前后两轴向应变片串联后接在同一桥臂(AB)上,而邻臂(BC)接相同阻值的补偿片。受拉时,两枚轴向应变片的电阻变化分别为
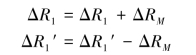
式中:ΔRM为偏心弯曲引起的电阻变化,拉、压两侧大小相等方向相反。
根据桥路原理,AB桥臂有
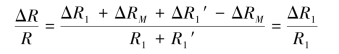
因此,轴向应变片串联后,偏心弯曲的影响自动消除,而应变仪的读数就等于试件的应变,即εp=εd(εp为轴向应变)。很显然,这种测量方法没有提高测量灵敏度。
3)串联后的半桥测量
如图1.4.2(c)所示,将两轴向应变片串联后接AB桥臂;两横向应变片串联后接BC桥臂,偏心弯曲的影响可自动消除,而温度影响也可自动补偿。根据桥路原理得(https://www.xing528.com)
![]()
式中:ε1=εp;ε2=-μεp,μ为材料的泊松比。
由于ε3、ε4为0,故电阻应变仪的读数应为εd=εp(1+μ),则有
![]()
如果材料的泊松比已知,那么这种组桥方式可使测量灵敏度提高(1+μ)倍。
4)相对桥臂测量
如图1.4.2(d)所示,将两轴向应变片分别接在电桥的相对两臂(AB、CD),两温度补偿片接在相对桥臂(BC、DA),偏心弯曲的影响可自动消除。根据桥路原理得
![]()
测量灵敏度提高了2倍。
5)全桥测量
按图1.4.2(e)的方式组桥进行全桥测量,不仅可消除偏心和温度的影响,而且使测量灵敏度比单臂测量时提高2(1+μ)倍,即
![]()
2.泊松比μ的测定
利用试件上的横向应变片和纵向应变片合理组桥,为了尽可能减小测量误差,实验宜从一初载荷P0(P0≠0)开始,采用增量法,分级加载,分别测量在各相同载荷增量ΔP作用下,横向应变增量Δε′和纵向应变增量Δε。求出平均值后,按定义便可求得泊松比μ,即
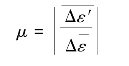
【实验步骤】
(1)设计好本实验所需的各类数据表格。
(2)测量试件尺寸。在试件标距范围内,测量试件3个横截面尺寸,取3处横截面面积的平均值作为试件的横截面面积A0,如表1.4.1所示。
表1.4.1 试件相关数据
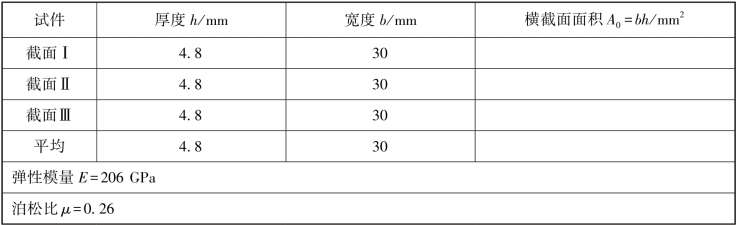
(3)拟定加载方案。先选取适当的初载荷P0(一般取P0=10%Pmax),估算Pmax(该实验载荷范围Pmax≤5 000 N),分4~6级加载。
(4)根据加载方案,调整好实验加载装置。
(5)按实验要求接好线[为提高测试精度建议采用图1.4.2(d)所示相对桥臂测量方法,纵向应变εd=2εp,横向应变εd′=2εp′],调整好仪器,检查整个测试系统是否处于正常工作状态。
(6)加载。均匀缓慢加载至初载荷P0,记下各点应变的初始读数;然后分级等增量加载,每增加一级载荷,依次记录各点电阻应变片的应变值,直到最终载荷。实验至少重复两次。相对桥臂测量数据表格如表1.4.2所示,其他组桥方式实验表格可根据实际情况自行设计。
(7)做完实验后,卸掉载荷,关闭电源,整理好所用仪器、设备,清理实验现场,实验资料交指导教师检查签字。
表1.4.2 实验数据

【实验结果处理】
(1)弹性模量计算
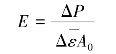
(2)泊松比计算
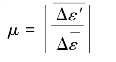
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




