如何应用10.6.5点覆盖方法？

1.基于树的点分配

参考文献（Mousavi et al.，2006）提出了一种一步部署（One-step Deploy-ment，OSD）分布式算法，它假定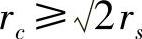。该算法将ROI均匀划分为二维正方形网格，每个网格边长为2r_s，命令传感器来占用所有网格点。直觉是如果每个网格点被一个传感器占用，则整个ROI实现全覆盖，同时传感器形成一个连通网络。

在OSD中，首先构建一棵宽度优先、树根在所选节点处的树，然后由树叶节点启动一次融合过程。在融合过程中，接收到包含所有子节点对应子树规模的消息后，节点计算树根在自身的子树，并向其父节点发送信息。融合过程之后，每个节点知道其子树的规模。然后，递归顶点分配启动。具体说来，树根节点选择其网格点（0，0）作为自己的部署目标，并使用网格点的匹配数，为每棵子树分配一个子区。每棵子树的根以同样的方式完成分配完成。当到达树叶节点时，这种递归分配结束。最后，每个节点知道其所指定的部署点，通过一步构建全覆盖，来移动到部署点。该算法采用一步运动策略，能够节约能量。但是，它要求在开始和树根选择时，所有移动传感器要处于连通状态，且要求树构建开销。

2.捕获和扩展

参考文献（Bartolini et al.，2008a）提出了一种捕获和扩展自部署算法，它隐式假设了ROI是有界的（虽然边界信息不是先验已知的），且存在足够的传感器来覆盖整个ROI。该算法在六角网格的六边形中心处安排传感器，六边形边长等于r_s。移动传感器通过选择其当前位置作为第一个六边形的中心，自发地在ROI上开始构建六边形网格，将其状态变为捕获，为自己分配0阶。

捕获传感器通过局部通信，知道其邻居的状态，并建立一个包含六边形中未捕获邻居的从属集。它将从属邻居推送到相邻空六边形的中心。然后，这些从属邻居处于捕获状态，主邻居为其分配一个比主邻居高的1阶。图10-9a说明了捕获活动，其中节点1捕获了其从属邻居（即节点2～9），将其推送到相邻六边形中心。

捕获活动之后，如果六边形中仍然存在备用传感器，会启动一个扩展过程，它将这些从邻居推送到具有较少传感器、较高阶数的邻近六边形，如图10-9所示。如果存在多个这种六边形，则选择最近的六边形。采用这种方法，冗余传感器通常被推送，以扩展六边形网格的边界。具有相邻空六边形的捕获传感器启动一次拉过程，本质上扩展了环搜索范围，并吸引来自于远处六边形的未捕获传感器。

当多个传感器独立启动算法时，可能会存在多个网格部分。这些网格部分可能没有相互对齐，因为它们是从任意点启动的。当两个网格部分会合时，启动早的网格部分将合并另一个网格部分。在合并的网格部分中，对捕获传感器节点位置进行了调整。调整从两个网格部分会合的边界开始，并传播到整个网格部分。

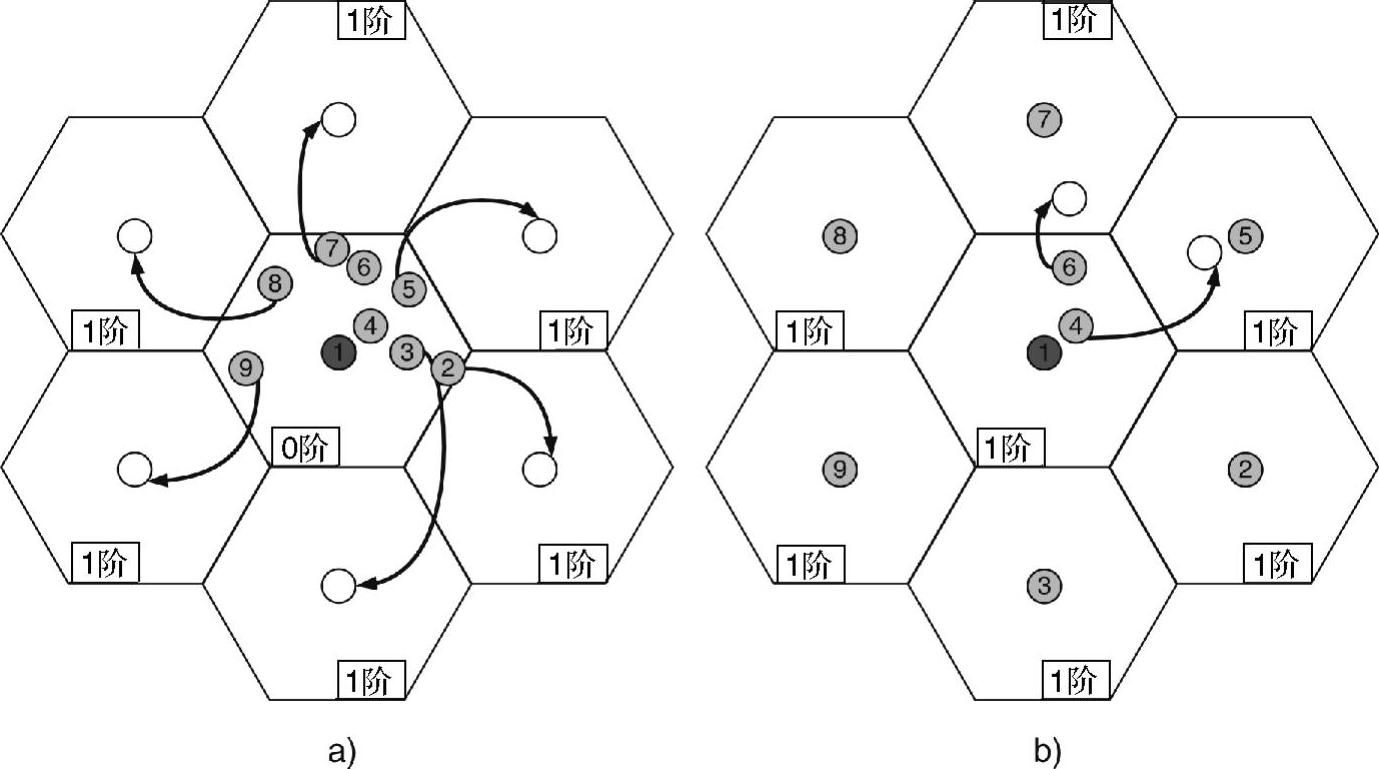
图10-9 捕获与扩展方法

a）捕获 b）扩展

与已经处于捕获状态的传感器相比，为了找到合适的部署位置，未捕获传感器在通信和移动方面，需要消耗相对较多的能量。为了平衡的传感器之间能耗，传感器有时可能会交换角色。当目标六边形的节点密度低于密度阈值时，可以通过禁止捕获和扩展活动来实现密度控制。(www.xing528.com)

根据参考文献（Bartolini et al.，2008b）提出的实现方案，该算法不属于纯粹的局部方案，因为在用于填充相邻空六边形的拉过程中，在发现未捕获传感器之前，捕获传感器必须访问（通过发送一条消息）最坏情况下的每个其他六边形。

3.组合贪婪旋转

参考文献（Li et al.，2008a；Li et al.，2009）介绍了聚焦覆盖问题。聚焦覆盖给定兴趣点的传感器区域覆盖称为聚焦覆盖。它可根据覆盖半径进行度量，即从POI到未覆盖区域的最小距离。最优聚焦覆盖能够实现覆盖半径最大化。作者们针对聚焦覆盖形成，提出了两种纯局部传感器自部署算法，即abbtextgreedy进度（abbGAD）和贪婪-旋转-贪婪（GRG）算法。

假设传感器节点随机部署在覆盖区域，且可能在开始阶段处于非连通状态。假定r_c≥3r_s，且传感器知道息的地理位置。问题是移动传感器节点形成一个围绕POI、具有等边TT布局的连通网络，用P来表示（如图10-10所示）。采用TT布局的原因是，该布局在保证网络连通性的前提下，当节点被部署在布局的顶点时，能够实现给定节点数覆盖面积最大化，且不存在感知空穴（Bai et al.，2006；Ma and Yang，2007；Zhang and Hou，2005）。

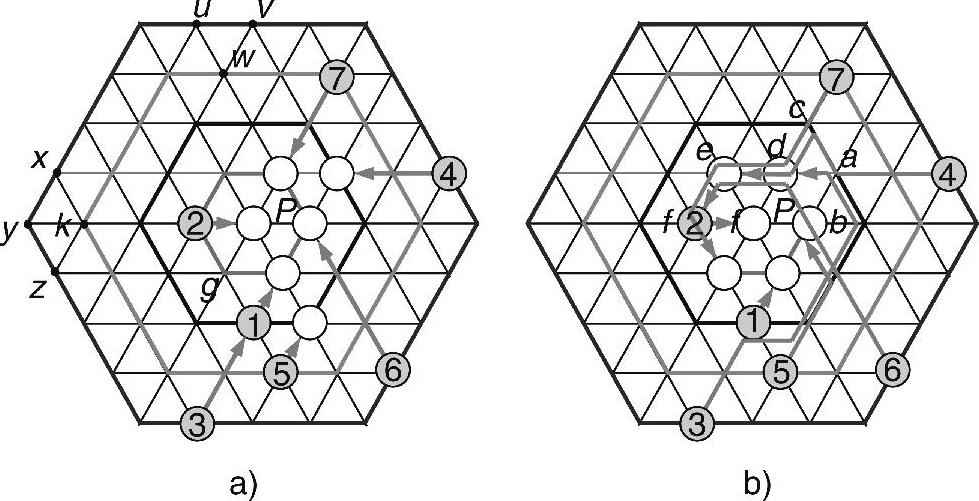
图10-10 等边三角形网格和聚焦覆盖形成

a）GA b）GRG

GA的基本思路是贪婪地沿着指向P的TT边移动节点。每个位于TT顶点的节点向另一个比当前节点更靠近P（图距离）的顶点运动。基于节点当前位置，对于节点运动来说，至多存在两种方向。位于角顶点的节点只有一种可能的运动方向。提出的这些规则主要用于运动控制。第一条规则用于确定同时从两个顶点到同一顶点的运动优先级。在图10-10a中，如果两个节点分别从x和y（或y和z）向k运动，高优先级将赋予从y（或z）出发的节点。但是，为了避免从x到z的潜在同步运动，第二条规则将禁止从z到k的节点运动。第三条规则允许位于与P相邻的六边形的任何节点向P运动，只要P未被占用。在图10-10中，节点轨迹用箭头线标记，它说明了GA是如何工作的。需要注意的是，在该实例中，节点3在节点5的初始位置停止。根据第二条规则，节点3不运动到顶点g，即使g是空的。

GRG包括贪婪进度运动和一种新型运动——旋转。当节点贪婪进度移动处于阻塞状态时，节点就会用到旋转。它将节点移动到同一层上的预定方向（如逆时针方向）。由于提出的算法不需要传感器节点的时间同步，因而某层中的节点旋转运动可能会阻塞高层（比P还高）中的贪婪进度运动。因此，引入一种暂停规则，用于在检测到高层存在一种相邻旋转运动时，取消节点旋转运动。在贪婪进度运动和旋转运动的目标是同一顶点时，采用竞争规则来为贪婪进度运动分配较高的优先级。人们提出三种更多规则，用于处理特殊位置节点（如角节点和网关节点）的运动问题。

GRG的执行过程如图10-10b所示。我们重点关注节点2、4、6。节点2采用单一贪婪进度步骤，运动到其最后位置P，而节点4和6沿着一条长的曲线路径运动。当节点4采用贪婪进度到达a后，它发现d已经被节点7占用，且指向b的贪婪进度被禁止。因此，它沿着其所在的六边形围绕P进行旋转。当节点4转动到c时，节点6到达b。此时，当节点7离开时，d变为未占用状态，因而节点4可以使用P。然后，节点2决定贪婪地向d运动，节点6决定旋转到d，从而导致d处发生碰撞。旋转节点6具有采取下一步部署步骤的较高优先级，它继续进行旋转，而节点2只得等待。最后，节点6通过e，旋转到最终位置f；当节点6离开e向f运动时，节点2旋转到e。

参考文献（Li et al.，2009）证明，GA和GRG能够在有限时间内终止，并得到一个具有最大覆盖范围且没有空穴的连通网络。事实上，它们是第一批能够提供此类保证的局部传感器自部署算法。仿真结果表明，GA的融合时间比GRG算法短，且能耗也比GRG算法低。在参考文献（Li et al.，2009a）中，由相同作者提出了一种称为OGRG的GRG优化版。OGRG采用部署六边形最佳逼近圆用于旋转，而不是六边形，因而能够保证圆形覆盖半径最大化。参考文献（Li et al.，2009b）提出了GRG的改进版，称为具有障碍渗透功能的GRG（GRG/OP）。GRG/OP安装有新型避障能力设备，不仅能够解决聚焦覆盖问题，而且还能解决传统的区域覆盖问题。