参考文献(Mousavi et al.,2006)提出了一种局部随机部署方法,称为Stanas-tic部署例程(Stanastic Deployment Routine,SDR)。在该算法中,传感器将被撒布在X×Y区域,根据受限随机游走获得的局部知识,它们将从密集区向稀疏区运动。SDR的执行独立于网络连通性。由于它的随机特性,SDR无法提供覆盖最大化、空穴消除或最终网络连通性保证。
在SDR中,时间被分成长度相同的连续时段。传感器节点在局部时段t,向某个位置随机运动,并在整个移动矩形(MRt)内被均匀提取。当节点运动时,MRt的位置发生变化,当t增加时,其尺寸动态减少。对于t≥0,MRt从东到西的宽度为X×p0×pt,其中0<p0<1和0<p<1是预定义常数。需要注意的是,MRt的尺寸仅取决于时间t。受到不断缩小的运动矩形限制,传感器在一个时间单元的最大运动距离,随着时间推移呈现指数规律下降,这保证了算法的终止。关键是确定每个节点在时段t处的MRt位置。正如我们将要在下面看到的,它可以由空中某个节点以局部方式完成。
假设在局部时段t,节点共拥有N个邻居(k跳邻居,k为常数)。假定Nw和Ne分别表示通过节点的位于南北线以西或以东的邻居数;Nn和Ns分别表示通过节点的位于东西线以北或以南的邻居数。于是,N=Nw+Ne=Nn+Ns。例如,在图10-8中,当实线节点位于位置a时,N=19,Nw=10,Ne=9,Nn=13,Ns=6。同时,假定dw,dn,de,ds分别表示从节点到其MRt西、北、东、南边界的距离。由于每个节点通常预计从稀疏区域向密集区域运动,因而MRt应当位于覆盖节点局部密集区域一小部分的位置。因此,定义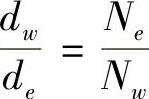 ,在这种情形中,
,在这种情形中,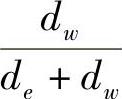 =
=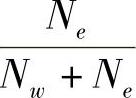 ,因而有
,因而有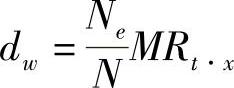 ,其中MRt·x表示MRt的宽度。同样,
,其中MRt·x表示MRt的宽度。同样,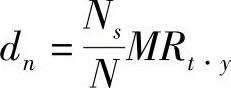 。
。
 (https://www.xing528.com)
(https://www.xing528.com)
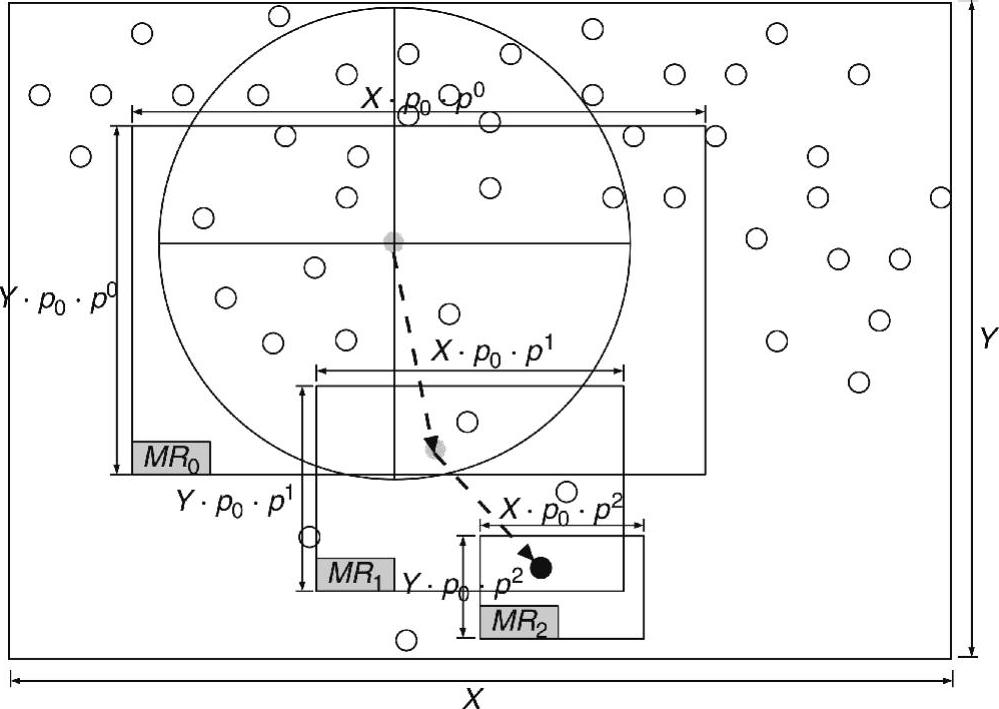
图10-8 基于MR的随机运动
在每个局部时段t中,每个节点能够计算MRt的尺寸及其在MRt的相对位置,即dw,dn,de和ds,因而当给定节点的自身地理位置时,它也能够计算MRt的地理位置。计算出MRt后,节点采用一定概率在符合均匀分布、尺寸减小的MRt内选择一个目标位置,并始终向该位置运动。然后,在局部时段t+1中,节点重复与其新k跳邻域信息有关的计算和运动。图10-8给出了运动步骤和某个节点在t=0,1,2时的MRt。需要注意的是,如果节点发现邻居数等于0(或小于具体数),即它将取消运动(减小其运动范围)。如果它们发现这么做能够减小其运动距离进而降低能耗,则两个相邻传感器可以交换其目标位置。最后,当每个节点的运动距离变小(如小于阈值)时,它停止运动。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




