协同执行器运动应用于节能传感器报告

参考文献（Liu et al.，2007）提出，移动机器人可用于在长期通信任务中节能（如视频监控）。在这种长期通信任务中，数据流是规则的，且为了采用更为节能的方式转发流量，流量足够大，以确保节点移动消耗的能量。给定源-目标对之间的通信要求，问题是如果有可能（使用当前机器人位置），找到二者之间的初始路由，并在路由上将每个节点移动到取其最终位置（如果可能的话，同时维护路由）。目标是在保持从中间节点（机器人）的初始位置到最终位置的运动距离最小的前提下，实现长期通信中节点的传输总功率最小化。

假设源S需要找到一条到达目标D的路由，根据参考文献（Goldenberg et al.，2004），中继节点的最佳位置必定均匀地分布在S和D之间的直线上。定理9-1给出了直线上相邻节点之间的最优跳数和最优距离。假定间距为d的两个节点，其发射和接收所需的能量与d^α+c成正比，其中α为常数（取值范围为2和6之间），c>0。d（S，D）表示S和D之间的欧氏距离。

定理9-1 （Stojmenovic and Lin，2001）：如果路由的最优跳数为k，使得k-d（S，D）×（（α-1）/c）1/α最小化，则从S到D的传输总功率是最小的，且相邻节点的最优距离d（S，D）/k。

证明：假设最初构建任意路径时，需要采用k跳。它的总长度不小于|SD|。因此，在不增加任意跳长度的前提下，路径上的节点可以沿着直线SD移动，从而降低了每跳的能耗。现在，考虑总长度为t两个连续跳，跳的长度分别为t-x和x。这两跳的总能量为（t-x）α+c+x^α+c。该函数一阶导数为零的点在x=t/2。这意味着当重传节点与路径上前一个节点和后一个节点相等的距离处时，能耗最小。因此，为了使得路由的总能耗最小，所有中继节点必须均匀分布在这条线上。于是，相邻节点的距离是d（S，D）/k。线上节点的传输总功率为k×（d（S，D）/k）α+c。假定x=d（S，D）/k表示线上相邻节点之间的距离，则总能量为d（S，D）×（x^α+c）/x。该函数的一阶导数在x值处为零

它能够使得线上节点传输总功率最小。因此

d（S，D）×（α-1）x^α-2-d（S，D）×c×x^-2=0

于是，我们得到

x=（c/（α-1））1/α

最优跳数k可以通过将d（S，D）×（（α-1）/c）1/α四舍五入到最接近的节点计算出来。线上相邻节点之间的最优空间为d（S，D）/k，它是（c/（α-1））1/α的一个凑整值。

基于定理9-1，参考文献（Liu et al.，2007）提出了两种路由算法，主要用于寻找从源到目标的最初路径。第一种算法称为最优跳数路由（Optimal Hop Count Routing，OHCR）。当前节点选择一个邻居，使得该邻居最靠近指向目标的进度最快的位置。仅考虑那些比当前节点更靠近目标的邻居。如果不存在进度的话，路由失效消息将从当前节点被报告给源节点。源S将d（S，D）×（（α-1）/c）1/α四舍五入到最接近的整数k，并计算到相邻节点的最优距离d（S，D）/k。如果k≤1，d（S，D）≤r，S直接向D传输消息。否则，S启动一次路由发现过程。如果不存在比u更接近目标的邻居，路由上的每个当前节点u将向S报告路由失效信息。否则，u选择一个前进邻居v，使得d（v，D）-d（u，D）-d（S，D）/k最小化。路由逐跳前进，直至到达目标D或出现路由失效。详细算法可正式描述如下。

最优跳数路由（OHCR）（Liu et al.，2007）

输入：S和D的位置，传输范围r。

输出：从S到D的一条路由。

开始

将d（S，D）/min（（c/（α-1））1/α，r）四舍五入到最接近的整数k；

计算相邻节点的最优距离d（S，D）/k；

if k≤0，d（S，D）≤r then

S直接向D传输消息，elseu=S；

While未到达D且没有出现路由失效时，do{

//对于当前节点u（u≠D）。

if {v|d（u，v）≤r，d（v，D）≤d（u，D）}=Φthen

u向S报告路由失效消息

else{

u选择邻居v，使得d（v，D）-d（u，D）-d（S，D）/k最小化；

u向v发送一个包含d（S，D）/k的路由发现数据包；u=v

}}

结束

一旦到达D后，即找到一条从S到D的初始路由。要求路由上的所有节点运动到其最佳位置。参考文献（Liu et al.，2007）研究了两种运动策略：多轮移动和直接移动。多轮移动策略用于参考文献（Goldenberg et al.，2004）提出的算法中。在每一轮中，每个节点（S和D除外）移动到路由上行节点和下行节点的中点处。它要求所有节点在每轮中都处于同步状态，以确保在移动时，维持连通性。如果在运动期间不需要连通性，或者在移动时可以通过拓扑来确保连通性，则可以使用直接运动策略来代替路由上节点多余的之字形运动可。在这种策略中，节点直接运动到最佳位置。

到D的路由可能包含不同的跳数，而不是规划数k，中间节点需要获知确切数，使得它们能够运动到合理的最终位置。D计算路径上相邻节点的实际位置，并将信息添加到路由确认数据包中，该数据包被路由回路由上的所有节点。当收到路由确认数据包后（S和D除外），每个节点根据添加的实际跳数计算其理想位置。相同数据包也可以同步节点，使得它们能够同时开始向最终位置运动。

参考文献（Falcon et al.，2009）提出了OHCR的一种变形，称为动态最优进程路由（Dynamic Optimal Progress Routing，DOPR），主要用于根据已经完成的实际进度和未来最优路由中的剩余节点数，来调整针对目标的最优进程。其算法可描述如下。

动态最优进程路由（DOPR）（Falcon et al.，2009）

输入：S和D的位置，传输范围r。

输出：从S到D的一条路由。

开始

将d（S，D）/min（（c/（α-1））1/α，r）四舍五入到最接近的整数k；

p=0；u=S；

While未到达D且没有报告路由失效时，do{

//对于当前节点u（u≠D）。

if {v|d（u，v）≤r，d（v，D）≤d（u，D）}=Φthen

u向S报告路由失效消息

else if p≥k

u选择最靠近D的邻居v；

u←v；(www.xing528.com)

else//（p<k）

DoP=d（u，D）/（k-p）；//路径上剩余节点的理想距离

U选择邻居v，使得dist（v，D）-dist（u，D）-DoP最小化；

p=p+1；u←v；}

结束

这里，p是路由中已经存在的中继节点数，而k-p代表将要添加到路径中的最佳剩余节点数。因此，DoP是动态最优进度（Dynamic Optimal Progress，DoP）。当p≥k，DOPR可以作为用于实现指向目标的最快进度的贪婪路由。

最小功率进度路由（Minimum Power over Progress Routing，MPoPR）（Liu et al.，2007）用于实现在选择转发邻居时，单位进度传输功率最小化。该算法的结构与前两种算法相同，主要区别在于选择最佳转发邻居的标准。这里，u选择邻居节点v，使得（d（u，v）α+c）/（d（u，D）-d（v，D））最小化。需要注意的是，d（u，v）α+c是用于选择v作为转发邻居的传输功率，d（u，D）-d（v，D）是节点v的距离进度。这个指标表示每单元进度的传输功率。它是成本进度范式（Stojm-enovic，2006）的一种。

在以前的算法中，只考虑那些比当前节点更靠近目标的邻居。如果这些邻居不存在，则报告路由失效。因此，算法仅对于密集网络是实用的。在稀疏网络中，恢复方案可以整合到参考文献（Falcon et al.，2009）的路由协议中。目标是使用DFS（Vukojevic et al.，2008）作为路由协议的内置故障恢复机制（也可见第4章）。总体思路如下。

在基于DFS的路由中，每个节点记忆它是否被DFS遍历访问过，且是否首次接收过发送方传送来的消息。它也监听来自于邻居的传输，以获知它们可能的访问状态。当前存储路由消息的节点将使用OHCR标准来排列其未访问邻居。选择列表中的第一个节点来转发消息。如果某个节点没有未访问邻居可以继续，则它将消息回传给发送方，发送方将消息转发给列表中下一个未访问邻居。最后，消息要么到达目标节点，要么返回源节点，不存在未访问或未搜索邻居。在前一种情形中，找到一条从源节点到目标节点的路由。后一种情形表示源节点和目标节点处于断开状态。将OHCR和DFS整合起来的OHCR-DFS的工作原理如下。

采用深度优先搜索的最优跳数路由（OHCR-DFS）（Falcon et al.，2009）

输入：S和D的位置，传输范围r。

输出：从S到D的一条路由。

开始

将S标记为已访问；disconnected_flag=0；

A=S；//A是当前保存消息的节点。

While未到达D且disconnected_flag=0时，do{

if A=S且S不存在未访问邻居

disconnected_flag=1；//S和D断开。

if A=S且A不存在未访问邻居

向其发送方A返回消息；A=向A传输消息的发送方；

if A存在未访问邻居

A使用OHCR标准来对所有未访问邻居进行排序；

A向列表中的第一个邻居B发送消息；

B将A记忆为发送方；

将B标记为已访问；

A=B；}

if disconnected_flag=0

报告路由失效；//未连通拓扑。

else

输出从S到D的路由；

结束

采用类似方式，可以将DOPR扩展到DOPR-DFS。需要注意的是，如果OHCR和DOPR运行成功，则OHCR-DFS和DOPR-DFS将输出与OHCR和DOPR相同的路由。但是，OHCR-DFS和DOPR-DFS适用于稀疏网络，且只要源节点和目标节点处于连通状态，就能保证路由被发现。

在图9-9所示的实例中，S发起到D的路由过程。首先，S将其自身标记为已访问，并根据OHCR标准来排列邻居A和F。假定A是列表中的第一个节点，即

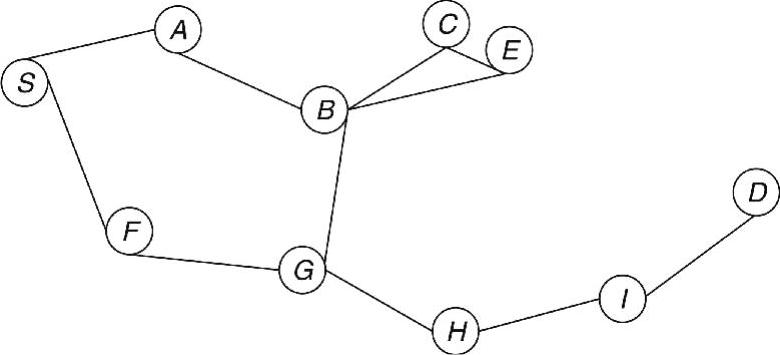
图9-9 OHCR-DFS的路由

|d（A，D）-|d（S，D）-d（S，D）/k‖<|d（F，D）-|d（S，D）-d（S，D）/k‖

其中，k为最优跳数，与能量效率有关。S将消息转发给A，A再将消息转发给B。B采用与S类似的方式来排列邻居C和E，并将消息转发给C。然后，C将消息转发给E。直到这一步，OHCR-DFS与OHCR工作过程几乎一样。由于E不存在未访问邻居，则OHCR将报告路由失效消息，路由在此终止。但在OHCR-DFS中，E将消息返回到其发送方（即C），C再将消息返回到B。需要注意的是，当E将消息以广播形式返回给C时，B监听E的访问状态。这样，B将消息转发给唯一未访问邻居G。最后，消息经由H和I到达D。因此，路由消息的轨迹是SABCECB-GHID，从S到D的路由是SABGHID。

参考文献（Falcon et al.，2009）进一步提出了采集k个邻居路由（Collect K Neighbors Routing，CKNR），用于处理源节点和目标节点处于非连通状态的网络。一旦计算出最优跳数k，节点可以简单地在整个图上运行DFS，直至它发现准确的k个节点。之后，所有k个节点直接运动到其理想位置。需要注意的是，它可能会出现k节点采集之前，节点已经到达目标的情况。在这种情形中，路由算法终止。

根据选择邻居时所使用的标准，我们有CKNR-OHCR和CKNR-DOPR。在CK-NR-OHCR中，转发节点的选择与OHCR-DFS相同。唯一区别是终止条件。一旦采集到k个节点，或者到达目标节点，则CKNR-OHCR终止；而在OHCR-DFS终止的条件是到达目标节点。因此，即使源节点和目标节点处于非连通状态，CKNR-OHCR也能找到k个节点，这些路由运动到预期位置，构建一个可行的路由。需要注意的是，CKNR-OHCR可能选择那些没有序列相邻关系的节点。为每个节点分配一个序列号（计数器），它代表移动后最终路由中的节点位置。

在图9-10中的实例中，假定最优跳数是k=6。S首先将自己标记为已访问，分配给它的序列号为1。根据OHCR标准，S对邻居A和F进行排序，然后将消息转发给A，为A分配的序列号为2。A将消息转发给B，为A分配的序列号为3。B对邻居C和E进行排序，然后将消息转发给C。然后C将消息转发给E，为C和E分配的序列号分别为4和5。由于E不存在未访问邻居，E将消息返回给其发送方（即C），C将消息返回到B。计数器不增加，直到B将消息转发给其唯一未访问邻居G，为G分配的序列号为6。路由算法终止，因为已经采集了6个节点。当G沿着路径向S回复一条ACK消息后，每个节点知道路由中的实际节点数。每个节点根据其序列号，计算其预期位置，并直接移动到该位置。在图9-10中，从S到D的最终路由是SA′B′C′E′G′D。

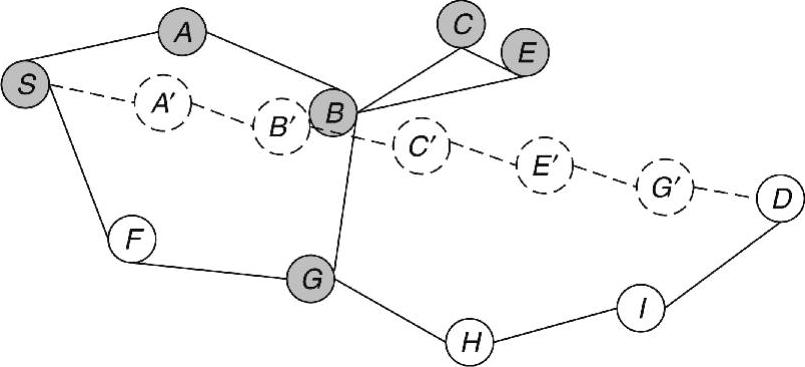
图9-10 CKNR-OHCR的路由