附加限制条件下的双连通图连通性问题

我们对上一节中的同样问题感兴趣，即从随机（但处于连通状态）拓扑开始，实现移动机器人的双连通性。但是，目标也是总覆盖区域最大化，同时实现网络直径最小化。假定每个机器人n有一个通信范围和覆盖范围。第一个参数用c（n）表示，它代表其他节点能够从c（n）接收消息的最长距离。第二个参数用s（n）表示，是代表机器人服务区域半径。例如，如果n是一个传感器，则s（n）对应于传感器的感知范围。如果n是执行器，则s（n）对应于n监视传感器的区域。这些范围之间的比值通常认为满足cr（n）＞2×sr（n）条件。网络的总覆盖区域定义为所有机器人覆盖区域的并集。显而易见，由于潜在的重叠，因而越靠近机器人，总覆盖区域越小。

网络的直径定义为任意两个节点之间的“最大”最短路径。更正式地说，如果d（u，v）是两个顶点u和v之间的最短路径长度，则图G=（V，E）的直径定义为max（d（u，v）∶u，v∈V）。由于直径限制了传输跳数，因而实现直径最小化成为大多数实时应用的关键。显而易见，越靠近机器人，网络的直径越小。因此，直径和总覆盖的概念看起来有点儿自相矛盾，且对于某个算法来说，可能是两个矛盾的目标。

图7-13使用包含4个双连通机器人的拓扑来说明这一点。在图7-13中，直径已经减小到极限（1），它导致网络区域大量重叠。如果我们采用同一网络，将节点移开，直至它们的覆盖区域不再重叠（图7-13b），则网络的直径变大（此处等于2）。但是，如图7-13c所示，一些几何组织（如三角网络）看起来在直径和覆盖区域之间，提供了一种有趣的折衷。

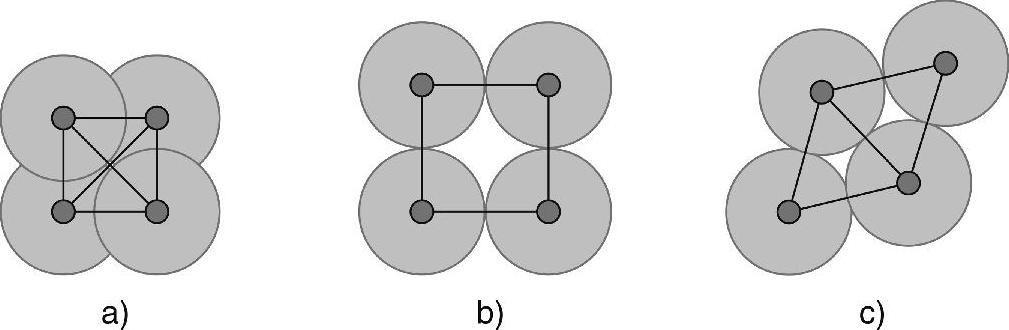
图7-13 三种配置实例

a）最大直径 b）最大覆盖区域 c）三角网络

因此，考虑到这种组织模式，它是一种不错的方案。但是，由于我们此处考虑的场景是节点最初已经部署，我们不需要在整个网络上构建这种完美拓扑（而是使用它来确定邻居节点的局部组织）。虽然如此，我们继续以图解的方式在整个网络上提出一些思路。使用这种结构，可以调节覆盖区域与网络直径之间的折衷，并在不改变组织几何构型（较短距离、较小直径、较高优先级）的前提下，调节邻居节点之间的距离。如图7-14所示。图7-14a给出了理想覆盖（直径为3）的方案，图7-14b给出了将网络直径减小为2（但存在覆盖区域重叠）时的方案。由于理想覆盖和理想直径之间的唯一区别是在不修改拓扑几何构型的情况下节点之间的距离，因而它表明仅使用局部操作可以实现部分折衷（如确定到直接邻居的局部距离）。

可以采用上一节提出的算法（Das et al.，2009），这样形成的网络具有较小直径和/或较高覆盖，它取决于给定的折衷参数。也可以对算法进行修正，用于在局部三角网络模式中，同时提高直径和覆盖两大标准。

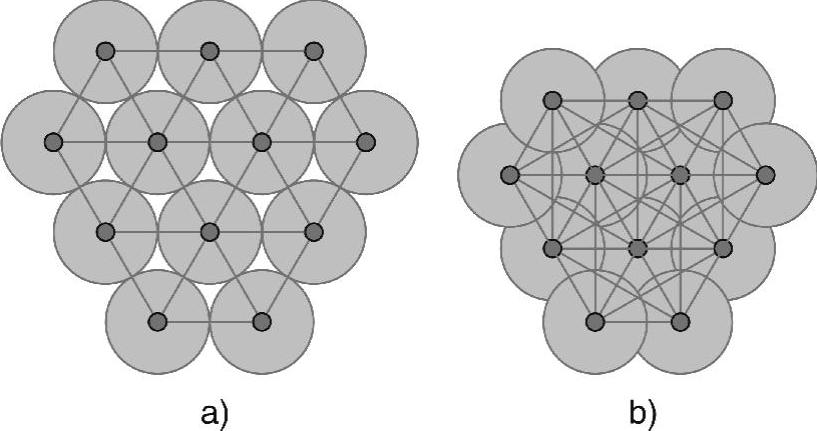
图7-14 折衷的不同选择

a）理想覆盖 b）理想直径

作为一种副产品，原始算法已经通过将机器人相互向对方移动，减小了网络直径。通过改变节点移动方式，可以进一步完善该算法。例如，不再简单请求两个节点移动一半间距来形成连通状态，节点可以首先检查有没有其他邻居，然后仅要求该邻居进行移动。更为一般的情况是，使具有比其他节点度数更低的节点移动，能够减小网络直径（尽管它也可能同时出现其他新问题）。(www.xing528.com)

一旦网络处于双连通状态，通过使用排斥力，可以实现一种局部三角网络，通过推开节点，使其间距相等，因而扩大了网络覆盖区域。这里，排斥力的范围可以作为覆盖和直径之间的折衷参数。图7-15给出了一种在原始算法后面应用这种排斥力的简单场景。一旦第一种算法终止，或者排斥力可以与算法合并时，即可采用这些排斥力。

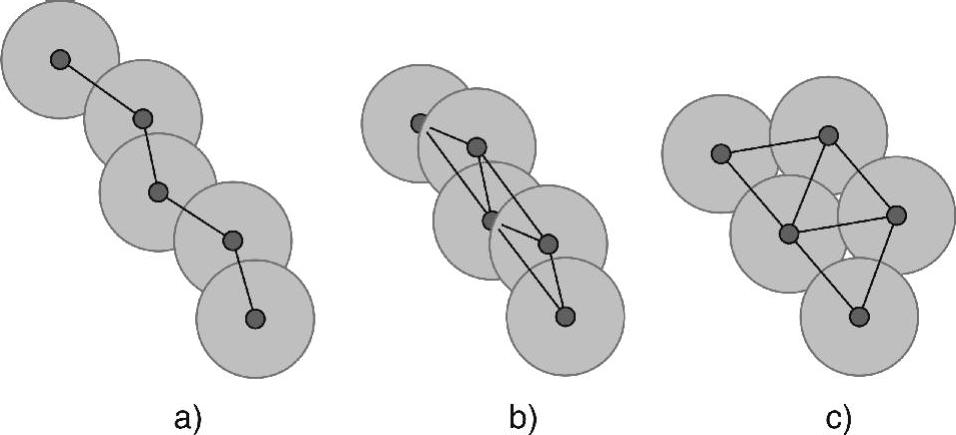
图7-15 混合双连通性和排斥力

a）初始拓扑 b）应用DLNS后 c）应用排斥力后

但是，在应用排斥力的过程中，应当仔细避免网络出现双中断的情况。需要注意的是，在移动传感器网络环境中，使用参考文献（Zou and Chakrabarty，2003）引入的虚拟力，可用于实现机器人总覆盖区域最大化。

在参考文献（Guang et al.，2008）中，作者考虑了一种不一定处于连通状态的初始网络，并提出了一种算法使其变为连通状态。它假定所有节点知道一个它们能够向该方向移动的公共位置（如基站）。每个到达该位置的机器人（如在基站范围内）洪泛一个数据包，使得每个接收到该数据包的节点知道它与其他节点处于连通状态。一旦所有节点处于连通状态，则可以采用虚拟力来实现网络覆盖最大化。

参考文献（Liu et al.，2009）提出了一种将处于非连通状态的初始网络转变为双连通网络的局部协议。目标是实现机器人移动距离最小化，同时最大限度地扩大网络的感知范围。它假定机器人具有一个公共通信范围和感知范围。每个机器人知道单跳邻居的位置和感知区域的边界。与前一种解决方案相同，所有机器人向下一个公共位置移动，且最大限度地扩大其感知覆盖范围。但是，节点移动时仅使用两种虚拟力。第一种虚拟力是能够将每个机器人拉向公共POI方向的引力，第二种虚拟力是能够在每对邻居节点之间使用的排斥力。同时使用这两种力量的应用是图7-16中的一个节点在中心位于POI（如图7-17中的POI，它是由有效的仿真结果产生的）上的双连通三角网格中结束。这是因为当节点进入平衡状态时，每个节点位于一个围绕POI的环路上。当钝角角度的方向发生一定数次的变化（称为振荡）时，每个节点明确停止移动。文献证明，如果网络处于稳定状态，则最终拓扑是双连通的，提出的协议具有高度可扩展性。该解决方案的另一个优势是除了每跳上所需的通信开销外，没有其他额外的通信开销。

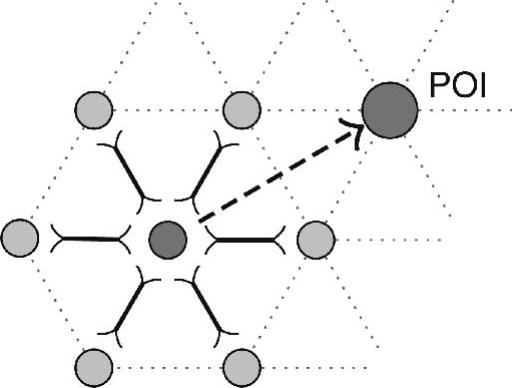
图7-16 邻近排斥力和POI引力

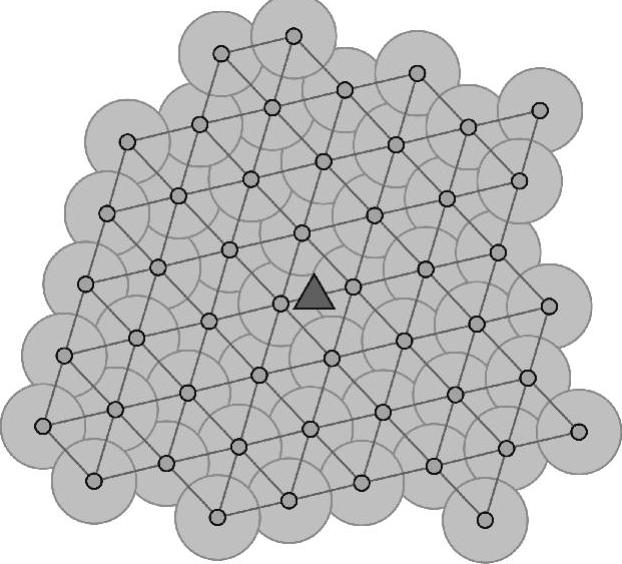
图7-17 由50个随机部署节点产生的拓扑