网络的性质简述

现在，我们讨论一些移动机器人已经随机部署、但仍然处于单连通状态的场景。从这个初始连通网络开始，我们的目标是仅使用局部移动决策将其变成双连通网络，并确保机器人运动距离之和最小化。本节提出的解决方案来自于参考文献（Das et al.，2009）。

从全局的观点来看，双连通网络是一种不包含任何临界节点和临界链路的网络，即如果单独删除任意节点或链路，网络仍然处于连通状态。由于链路是临界的，仅当链路的至少一个端点是临界的，使网络保持双连通状态需要将每个临界节点转变为非临界节点。通过观察图7-11，显而易见，节点（如N）的全局临界性无法以局部的方式来确定，因为它与某些远距离边（如AB）有关，这些边的存在情况是局部无法获知的。

该算法基于p跳临界性概念，我们已经在第7.6节中进行了讨论。实际上，假定每个节点能够以多跳方式交换和中继问候消息，来采集其p跳邻居信息。如果对于某个节点n来说，其p跳区域在n不存在的情况下处于断开状态，则n能够以局部方式确定它是p跳临界的（我们在下文简单地称它是临界的）。在图7-11所示的实例中，N将确定它是临界的（除非p≥5）。

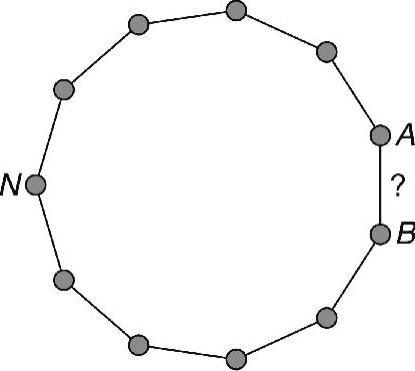
图7-11 局部临界节点与全局临界节点

根据定义，任何临界节点的移动都可能会导致网络处于断开状态。于是，该协议的基本思路是仅使用非临界节点来生成双连通网络，而使临界节点处于静态（直到这些节点变成非临界节点，才能够移动）。这样，算法基于临界节点根据实际情况来触发非临界邻居的预定义行动小集合。特别是临界节点存在或不存在，其他临界邻居将产生不同动作的事实。在描述这些之前，我们再定义几个概念。

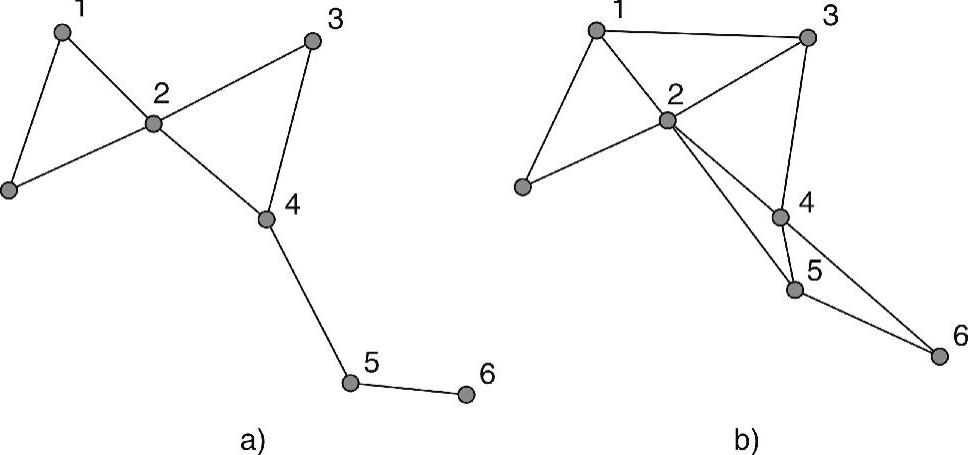
图7-12 引自参考文献（Das et al.，2009）的算法简单场景

a）初始网络 b）最终网络(www.xing528.com)

如果某个临界节点至少具有一个非临界邻居，则我们称该临界节点是可用的。换句话说，如果某个临界节点至少具有一个可以移动的邻居，则我们称该临界节点是可用的。可用性概念可用于确定某些临界邻居中哪个临界邻居可以引导局部行动。更准确地说，这种情形中的导航节点（也称为临界头）必须可用，且要具有比其他任一可用临界邻居大的ID（以防止打结）。我们考虑图7-12a中的实例，节点2、4和5都是临界的。由于4比2大，且节点4是可用的，因而节点2不是临界头。由于5比4大，且节点5是可用的，因而节点4也不是临界头。这里，节点5是唯一的临界头。需要注意的是，如果节点2的ID比节点4大，就可能会出现两个临界头（节点2和节点5），而不是一个临界头的情况。

该算法的工作原理如下：在初始化阶段，每个节点检查它是不是p跳临界点，并在每次问候消息交换完毕后，继续检查它是不是p跳临界点。一旦某个节点检测到它是p跳临界点，它将向所有直接邻居广播一条临界公告数据包，包含它的可用性信息。于是，可能会出现两种情况：

（1）如果该节点没有临界邻居，则它选择两个属于独立“双连通组件”的邻居，并要求它们互相向对方移动。如果n₁和n₂之间的距离是d，则每个节点可以移动的距离为（d-r）/2，其中r是通信范围。为了防止出现多种可能方案，通常选择能够实现d最小化的那对邻居。

（2）如果该节点有一个或几个其他临界邻居，则它需要算出临界邻居是不是临界头。如果是，则它请求非临界邻居向另一个临界邻居移动。这里，所选的邻居应当移动的距离为d-r。与前一种情况类似，选择都属于独立“双连通组件”、且间距d尽可能小的一对节点。

如果某个节点在移动过程中接收到一个行动请求，则它简单忽略这条请求；如果它同时接收到来自于不同邻居的多条请求，则它考虑来自ID最大的邻居请求。需要注意的是，由此形成的运动可能无法在每个预期地点生成一条新链路，例如当一个节点向另一个节点移动，但另一个节点向别处移动时，就会出现这种情况（在情形1中）。但是，由于算法是渐进式的，因而这种情况有望在后面的迭代过程中得到解决。

我们再次考虑图7-12给定的网络，来描述将初始网络（图7-12a）转化为（图7-12b）的执行顺序。如前所述，节点2、4、5初始状态是临界的，但只有节点5是临界头。于是，节点5通过请求节点6向节点4移动，成为第一个行动节点。然后，节点5变成非临界节点，节点4成为临界头，请求节点5向节点2移动。最后，节点2成为唯一的临界节点，当网络处于双连通状态后，它通过请求节点1和节点3相互向对方移动，来应用第一种情形。

作者们通过实验，将该算法与集中式算法（Basu and Redi，2004）进行了对比。仿真结果表明，当采用局部算法时，机器人运动的总距离大大缩短（对于节点密度为10的网络来说，集中式算法中机器人运动总距离大约是该算法的2.5倍）。