非受控动态拓扑中的生成树算法探究

下面讨论涉及传感器以一种非受控方式进行移动的场景，例如传感器安装在所考虑场景的一些物理载体（如运动由外部参数决定的动物、车辆、虚拟昆虫等）上时就会出现这种情形。在最近几十年内，动态拓扑上的分布式生成树维护问题已经得到了广泛的研究，尤其是在动态图和移动Ad Hoc网络两个研究领域。为了更好地理解该问题，绝大多数方法，如果不是所有方法，都考虑了通过构建单个生成树，来覆盖整个网络。通常情况下，从自稳定的角度来解决问题，这些方法将拓扑事件认为是诱发非法状态的故障，且必须对算法进行修正。然后，当整个网络被单个树所覆盖时（这属于合法状态），即可实现算法的修正。为了给此类算法提供一些参考，人们引用了参考文献（Awerbuch et al.，1993）中的分布式图形算法，它“从零开始”给出了最短构建时间（最近又在参考文献（Burman and Kutten，2007）中被修改用于消息传送模型，在参考文献（Gaertner，2003）中用于描述可比算法数）。

虽然大多数算法在每次拓扑失效后，都会重新开启一次完整的树重构过程，但其他一些更为现实的方法（如（Baala et al.，2003）、（Abbas et al.，2006）等）试图纠正由链路失效导致的局部偏差。然而，这些算法仍然需要一些稳定时间，在这段时间内独立子树是不可用和不一致的。一种严重后果是，它们根本无法简单处理比稳定时间变化快的拓扑。

迄今为止，我们讨论了要求整个网络处于连通状态的场景。但事实并非总是如此。实际上，传感器与执行器网络的大多数应用并不要求传感器和所有执行器之间都存在一条路径，关键是传感器必须能够向至少一个执行器（考虑到容错，也可能是几个）报告信息，或与至少一个执行器进行通信。另一方面，这种通信通常是可达的，即基础支撑结构始终是可用的，这一点至关重要。

最近的一篇论文（Casteigts et al.，2009）提出了一种处理高度动态拓扑问题的新方法。该方法的基本思路是放弃构建覆盖整个网络的单一树，而是考虑维护由多棵树构成的森林，它能够机会地发生变化。当任何拓扑失效后，若给定破树的两个部分仍然透明可用，则可以采用单一操作来恢复一致性状态。实现这种特性的关键点是树的合并和拆分必须完全是局部事件，不能产生任何波传播。该算法依赖于令牌循环，必须严格保持每棵树上的令牌数。与其他基于令牌的方法区别在于每个令牌的传输仅限于树的边缘，树的边缘可以提供一些非常特别的属性。主要性能是每个节点随时知道哪个局部边导致令牌丢失，该边是前一次访问结束后，该令牌出来时经过的那条边。结果表明，当树的某个边被破坏时，两个端点节点中的一个知道树的剩余部分是免令牌的，且知道当前它是导致令牌丢失的路由上的“最高”节点。因此，它能够局部生成一个新令牌，重新为其他节点透明恢复地令牌循环过程。

该算法的原理可以通过一个小的局部修改模式集来进行详细描述，如图7-5所示。最初，每个顶点是一个单顶点树，它有自己的令牌（标签T）。当两个令牌位于相邻顶点时，它们将进行合并，对应边标记为树边（规则r₃）。这种标记在每一面上使用不同的值（1和2）来反映剩余令牌诱发的方向变化。如果没有合并是局部可达的，则将令牌传输到树中的任意邻居（规则r₄），然后对方向标记相应地进行更新。对于每个给定节点，如果局部边导致令牌破坏，则以局部方式重新生成新令牌（规则r₁）。破坏边的另一面不执行任何特定操作（规则r₂）。(www.xing528.com)

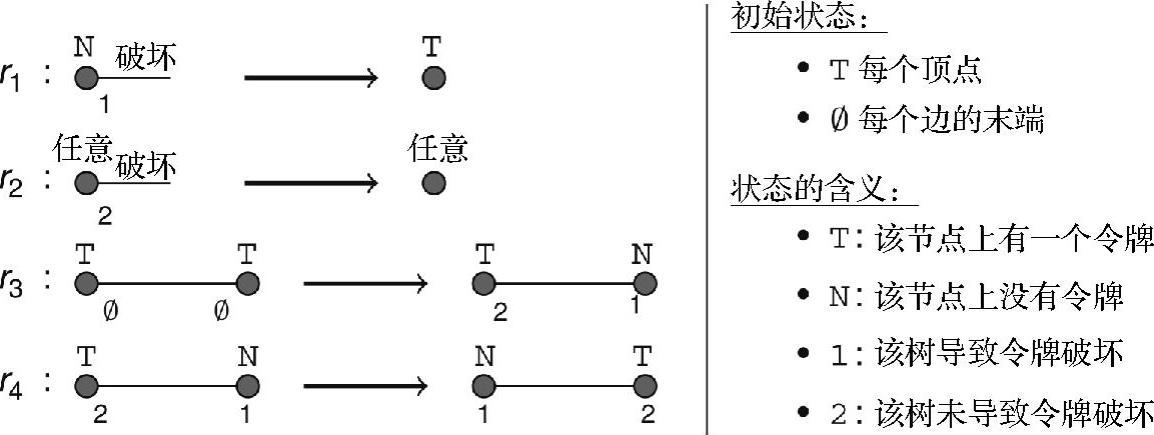
图7-5 生成森林算法

传感器和执行器网络环境中一个有趣的问题是树的预期尺寸是否足够大，以保证每个传感器任何时候在它的树中至少有一个执行器。换句话说，人们可能想要回答如下问题：“给定传感器数目、密度和拓扑预计变化速率，需要多少执行器，使得每个传感器在树上至少拥有一个执行器的概率高于给定阈值？”在参考文献（Casteigts et al.，2009）中，作者们通过描述两个给定树的预计合并时间（它是树尺寸和树之间可用链路数的函数），提供了初步解决方案。尽管这些初步结果与完整答案之间还有很长一段路要走。