最小生成树局部近似值的优化方法

局部最小生成树（Localized Minimal Spanning Tree，LMST）是由参考文献（Li et al.，2003）引入的，我们在第2章已经进行了讨论，它是一种仅采用局部信息来逼近MST的分布式结构。更准确地说，假定每个节点u可以从其单跳邻居处采集正确信息，然后计算能够覆盖自身和其单跳邻居（包括这些邻居之间的边，可以从其位置信息中推导出来）的局部MST。这样，当且仅当边（uv）属于u和v的局部MST时，它属于LMST。为了便于说明，相对于图7-1给出的最优解，我们在图7-2中给出了采用这些算法得出的结果。由此可以看出，只生成了几个循环（3个）。考虑到仅使用了单跳信息，这种近似算法性能比较好。

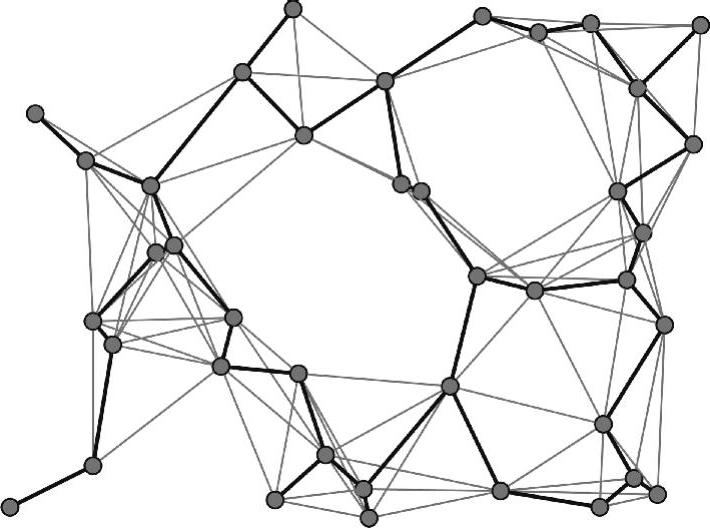
图7-2 局部最小生成树(www.xing528.com)

基于彭罗斯的观察结果——MST最长边对应的最佳传输范围值，参考文献（Ovalle-Martinez et al.，2005）提出使用LMST算法来寻找该值。更准确地说，基本思路是在内部采用波传播，来找到最长的LMST边（逼近该值的）。但是，论文提出，在他们不到3%的实验（网络节点数可达500个）中，即使添加少量边（如图7-2中那些生成循环的边），也可能会将节点传输范围值扩大约33%。反过来，这33%的传输范围变化值会导致能耗增加50%，甚至更多，这取决于所采用的功率衰减因子。因此，论文提出了一种用于删除LMST多余边的准局部方案，采用该方案，每个节点要发送的消息平均数小于7。该过程是一个环路破坏过程，它重复沿着从树叶到树根的悬垂边进行。通过删除它们的最长边，环路被破坏。该过程持续进行，直至它们在同一节点处结束，可以认为该节点是事实上的主导者，它可以学习该过程中最长边的值，并将其以广播形式发送给其他节点。该过程仅在二维空间内运行，因为它是基于面路由方案（关于面路由的详细信息见第4章）。