节点重定位策略：基于能量稀疏区的临时改变方向与历史事件预测

根据第6.2节中引入的能量模型，汇聚节点在向数据源移动时，应当缩短路径长度，从而降低和平衡能量消耗。在重定位期间，汇聚节点可能需要持续接收数据。这会给受访区域内的节点带来额外负荷，增加了能耗。因此，理想情况是汇聚节点经过能量密集区，而不是能量稀疏区。基于这种考虑，参考文献（Bi et al.，2007）提出，在汇聚节点进入能量稀疏区之前，通过采用特定策略，可以临时改变其移动方向，然后返回转向重定位目标。

多汇聚节点最佳配置是NP完全问题，因为它等价于单位圆盘图上的NP完全支配集问题（Bogdanov et al.，2004）。在下面各节中，我们将介绍一些文献中提出的典型汇聚节点重定位策略。

1.基于簇的方法

参考文献（Banerjee et al.，2009）研究了使用多个移动汇聚节点分簇的WSN中的汇聚节点重定位问题。文献假定每个传感器加入一个且只能加入一个最近的簇，并向相应汇聚节点（簇头）发送数据。汇聚节点形成一个连通覆盖网络，用于数据深度融合到固定基站。假定汇聚节点最初分布理想，使得每个簇覆盖网络区域的面积大致相同，且没有大的重叠，这样整个网络完全被覆盖。一旦构建完成，簇将保持不变。

汇聚节点只能在自己的簇内移动。在移动时，它们在覆盖网络中重复执行路由发现过程，以保持一条指向基站的路由。如果没有发现路由，则它们返回前一个位置。这种连通性保持方法可以通过使用单跳或两跳区域信息进行改进。作者通过对第6.2中引入的能量模型稍作修改，分析了当汇聚节点随机独立地进行移动时的网络能耗。他们提出了三种受控汇聚节点移动性策略。

在基于剩余能量的策略中，汇聚节点通常移动到所在簇的剩余能量中心，以平衡能量消耗。剩余能量中心是根据剩余能量衡量的簇成员（传感器）位置的平均值。每个簇成员向汇聚节点发送其剩余能量水平和局部能量消耗估计值（基于历史数据），然后汇聚节点在需要时预测相应传感器的能量。剩余能量中心可能会远离事件的当前位置，导致数据传输距离增加，从而导致总能耗提高。

在基于事件驱动的策略中，汇聚节点通常向所在簇中的事件区域移动，即数据流量最大的区域。目标是缩短数据传输路径，降低传感器中继消息开销，最终延长网络生存周期。但是，在汇聚节点到达事件中心后，它将停在那里。在这种情况下，中继节点集保持不变，避免再进行能量平衡。

由于这两种策略存在着局限性，作者进一步提出，将二者结合起来，得到一个混合策略。汇聚节点首先向事件中心移动，然后向能量中心移动。当汇聚节点离开事件中心时，另一个汇聚节点移向事件中心，感知事件的传感器将向汇聚节点报告数据，从而产生更大的能量增益。

2.事件驱动方法

参考文献（Vincze et al.，2007）研究了事件驱动WSN中的单汇聚节点重定位问题。在事件驱动网络中，传感器具有相同的感知半径，且当传感器检测到事件时，它们即变成数据源。数据源使用最短路径，通过消息中继向汇聚节点发送感知数据。其他传感器不传输数据。事件可建模为以固定速率、随机方向移动的入侵者。假定感知域是一个圆形区域，传感器均匀分布且足够密集，这样每条源到汇聚节点路径近似看做是一条直线，且由长度相等的若干跳组成。

通过近似方法，作者证明，对于某个事件来说，节点P的平均传输负荷（转发消息负荷）L_P与P和事件之间的距离成正比，与P和汇聚节点之间的距离成反比。作者还证明，当P距离汇聚节点只有半跳时，L_P最大。然后，从汇聚节点的角度来看，负荷最重的传感器位于指向最远事件的方向。

基于上述结果，作者认为，为了实现总能耗最低，需要通过重定位汇聚节点，实现事件距离的最小化。这等价于著名的“设施选址”问题。作者进一步提出，为了在节点间平衡能耗，最大传感器负荷应当实现最小化。也就是说，实现事件到汇聚节点之间的最大距离最小化。在直线路由的情况下，这等价于“最小覆盖圆”问题。

作者提出汇聚节点可以根据历史事件数据，来预测当前事件的未来位置，并提前做出重定位决策。一旦计算出目标位置，汇聚节点将移动到那里。当事件随着时间改变位置时，汇聚节点将根据当前事件的演进，来不断调整其位置。

3.蛮力方法

参考文献（Friedmann and Boukhatem，2009）提出了一种针对多汇聚节点重定位的集中式蛮力算法。周期性运行该算法来检查是否应当对汇聚节点进行重定位。当且仅当新汇聚节点位置导致总能耗降低时，汇聚节点重定位就会发生。假定汇聚节点具有网络的全局视图，因而能够运行集中式算法。(www.xing528.com)

为基础网络图的每个边，在两个传输方向的每个传输方向上分配一个权重。权重与两个因子之和有关，这两个因子分别是：接收节点剩余能量的倒数，使用各自系统平衡后，消息沿着边进行传输时的能耗，当节点剩余能量不断减少时，边权重随着时间发生变化；集中式源路由方法（如Dijkstra算法）用于找到从每个传感器到它最近的汇聚节点的最短路径（即具有最小加权和的路径），这种路径试图避免使用能量稀缺节点，降低沿路径用于消息传输的总能耗。

为了最大限度地降低网络中的能耗总量，汇聚节点应当放置在能够实现总能耗最小的位置。总能耗可以根据所有最短路径的加权和来度量。在计算总能耗时，指向汇聚节点的、链接主动节点（即那些正在感知和传输数据的节点）的路径权值有意增加，来使得汇聚节点靠近主动节点，降低用于消息中继的能耗。

启发式方法可用于寻找汇聚节点最佳位置。在这种方法中，每轮重定位仅限于几个（1、2或3个）汇聚节点，且在这些情况下，找到最优方案。为了进一步缩小搜索空间，只允许汇聚节点在8个方向上移动：北、南、东、西、东北、西北、东南、西南。作者考虑了过渡效应（在重定位期间，通信开销可能临时增加）。汇聚节点使用多步移动，而不是一步直接移动到最佳位置，每一步都是在有界局部区域内由受限本地搜索确定的。

4.基于MILP的方法

参考文献（Basagni et al.，2008）研究了单汇聚节点重定位问题，并将其建模为混合整数线性规划（Mixed Integer Linear Programming，MILP）问题。感知区域被划分为二维网格。网格点集S，称为汇聚节点站点，是汇聚节点可能访问的候选位置。汇聚节点逐步移动，在预定范围d_max内，每一步到达一个站点。它必须在每个站点停留至少t_min个时间单位。当汇聚节点访问时，它被认为是不可达的，因而传感器保存数据，不进行传输。可以通过调整网格划分的粒度和d_max值，来调整保持时间。汇聚节点使用网络范围内的洪泛，来向传感器通知其位置及其可达性。

汇聚节点站点集S和最大步移距离d_max定义了一个图。MILP问题用于确定图上的初始汇聚节点站点、汇聚节点重定位路径、汇聚节点在每个站点k处的逗留时间t_k，以使得目标函数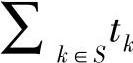最大化。目标函数描述了网络有效生存周期，即传感器能够传输报告的时段。它受到多种因素影响。例如，节点用于数据传输和路由产生的能耗不能超过其初始能量。

基于整数线性规划（Integer Linear Programming，ILP）的集中式解决方案是不可扩展的。对于大型网络来说，在单个节点上采集网络信息的成本和运行ILP解决方案的计算开销增长迅速，使得这些方案仅适用于包含几十个而不是数百个节点的网络。除了基于MILP的集中式解决方案之外，作者还提出了两种局部汇聚节点重定位策略：贪婪最大剩余能量（Greedy Maximum Residual Energy，GMRE）策略和随机运动（Random Movement，RM）策略。汇聚节点移动到邻近站点，该站点的传感器拥有最大剩余能量；后者要求汇聚节点移动到随机选择的邻近站点。

5.外围的方法

根据参考文献（Luo and Hubaux，2005），当WSN覆盖区域为圆形，且采用最短路径路由时，最优汇聚节点移动性策略是沿着网络外围移动。根据这个结果，参考文献（Hashish and Karmouch，2009）建议沿着网络外边界部署汇聚节点，并提出一种简单的汇聚节点重定位方案，来处理由汇聚节点附近节点能量消耗快导致的汇聚节点划分问题。

在提出的方案中，初始阶段对网络外边界进行识别。汇聚节点将边界分为许多部分。图6-8给出了一种包含4个汇聚节点S₁，…，S₄的圆形网络，4个汇聚节点将外边界（边界节点突出显示）分成4个部分。在每个部分中，每个边界节点在两个方向上，保持到最近汇聚节点的跳数。选择汇聚节点来计算网络的虚拟中心（v-center）。给定预定义参数h，距离最近汇聚节点k×h（k=1，2，…）跳的边界节点将其位置信息发送给汇聚节点。来自于所有汇聚节点的报告（以聚集形式）在所选汇聚节点处进行采集。然后，所选的汇聚节点计算虚拟区域的中心，这些节点将该中心定义为v-center，然后使用v-center的位置信息来洪泛整个网络。在图6-8中，计算出来的v-center靠近感知区域的中心。

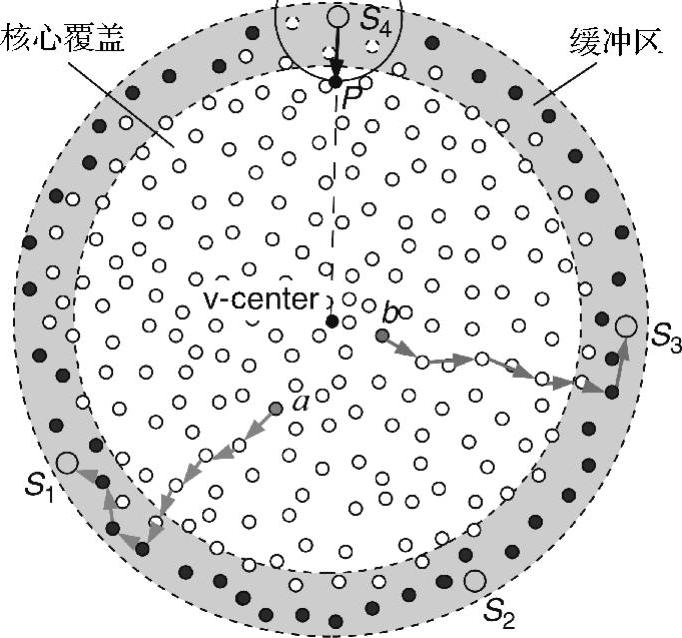
图6-8 汇聚节点部署、源到汇聚节点路由和汇聚节点重定位

当传感器检测到某个事件时，它采用定向转发，将事件数据从v-center发送到外边界上。当边界节点接收到传感器数据后，它将数据沿着网络边界转发给最近的汇聚节点。采用这种数据分发方法，图6-8中的两个数据源a和b，分别向汇聚节点S₁和S₃发送数据。当汇聚节点位于边界上时，边界节点能量消耗速率要比内部节点快，导致所谓的脱皮现象。如果汇聚节点发现它被网络隔离，或单跳邻居数很少，或低速率接收数据，则它向v-center移动一段与传输范围相等的距离，以维护连通性。例如，在图6-8中，由于汇聚节点S₄的3个邻居全部电池耗尽，因而S₄决定移动到位置P。

不受欢迎的脱皮现象会导致覆盖率的降低。为了确保覆盖面，作者建议沿着核心覆盖区域，使用更多传感器或更大缓冲区（图6-8中的灰色区域）。基于第6.2.2节引入的能耗模型，作者认为，提出的汇聚节点重定位方案会导致次优能量平衡。