直接接触数据采集技术

在直接接触数据采集中，移动汇聚节点以单跳通信方式，直接从数据源处采集数据。汇聚节点可能会重传数据，或者在需要时从物理上将数据传送给固定基站。这种方法能够实现传感器通信能耗最小化，因为传感器之间不需要相互转发数据。在这种场景中，主要问题是计算汇聚节点最佳轨迹，该轨迹覆盖了所有数据源，且能实现数据采集延迟最小化。

1.随机数据采集轨迹

参考文献（Shah et al.，2003）研究了汇聚节点随机移动性问题，并提出了一种简单的数据采集算法。在算法中，传感器将测量数据缓存在本地，等待移动汇聚节点到来。文献也分析了多汇聚节点场景。每个汇聚节点随机移动，在通信范围内遇到的传感器处采集数据。然后，汇聚节点将采集数据传送到无线接入点（如固定基站）。

在汇聚节点随机移动的情形中，传感器端的能耗主要是由汇聚节点发现和后续数据传输 产生的。假定每个汇聚节点在移动时广播一条信标消息。发现汇聚节点的最简单方法是对无线通信信道进行监测。一旦传感器接收到信标消息，则它可以断定汇聚节点到来。但是，连续进行信道监测的能耗比较高。参考文献（Chakrabarti et al.，2003）提出，如果汇聚节点（如安装在往返班车上）沿着规则路线移动时，则传感器可以通过学习汇聚节点的运动规律曲线来预测它们的到来。

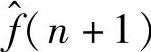找到汇聚节点后，数据传输也能够以一种智能的方式进行。如果传感器发现汇聚节点后，简单地进行数据的传输，则数据可能无法成功交付，或者要进行许多重传，从而导致能量浪费。根据参考文献（Anastasi et al.，2007a），消息丢失概率会随着传感器与汇聚节点距离的缩短而降低。假定汇聚节点沿直线经过传感器。为了实现能耗最小化，数据传输应当发生在消息丢失概率最小的时段内，该时段正好位于传感器与汇聚节点最小距离点附近。基于这种考虑，参考文献（Anastasi et al.，2007b）提出了一种自适应数据传输协议。在参考文献（Anastasi et al.，2007b）中，可以根据函数估计第（n+1）次通过时的接触时间，其中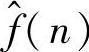和α（0＜α＜1）代表上次（第i次通过）接触消耗时间，接触持续时间或接触与数据传输之间的时间间隔，或其他相关度量标准（不同度量标准具有不同的函数和参数）。根据估计结果，传感器在恰当时间开始传输数据，并发送预定数目比特。如果接触时间足够长，在传输数据之前，传感器能够执行一次休眠-唤醒循环，则这么做以节省能量。

2.TSP访问数据采集

当汇聚节点移动性是一种可控因素时，我们可以通过合理选择汇聚节点轨迹，来降低数据采集延迟。不难发现，直接接触数据采集这个NP完全问题（Lawler et al.，1985）通常等价于旅行商问题（Traveling Salesman Problem，TSP）。在非正式情况下，TSP问题是：给定城市（即传感器）数，找到最短旅行路线，使得每个城市（传感器）恰好被访问一次，并返回出发城市。

参考文献（Nesamony et al.，2006；Nesamony et al.，2007）将汇聚节点移动问题看做是TSP的一个变形，称为使用邻居的旅行商问题（Traveling Salesman Prob-lem with Neighborhood，TSPN），其中汇聚节点需要对每个传感器的邻居进行一次访问。直觉是为了从传感器处获取数据，汇聚节点只要位于传感器的通信范围（模型为圆盘）就足够了。图6-3a将TSP访问（粗虚线）和TSPN访问（粗线）进行了对比，包含1个移动汇聚节点和4个传感器。

图6-3 TSPN

a）使用邻居的TSP b）点集计算

在参考文献（Nesamony et al.，2007）中，作者提出了一种寻找汇聚节点最佳可能访问路线的算法。该算法要求所有传感器的位置是已知的。它首先确定圆盘的访问次序。在这个过程中，可能会用到一些排序限制条件。例如，必须首先访问那些电池能量即将耗尽的对应传感器，以防止数据丢失。如果不存在限制条件，则最直观的方法是基于代表点的TSP顺序来对圆盘进行排序。可以使用不同方式来选择圆盘的代表点。例如，它可能是一个随机点、中心点或距离起点最近的周边点。

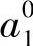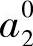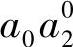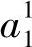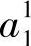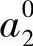一旦确定了访问次序，即可计算最优点集。初始集是由起点a₀和第i个圆盘C_i的代表点a_0i构成。然后，更新为与a₀，和圆盘C_i有关的的过程如下：如果直线与圆C₁相交，则是交线上的任意点。否则，是圆C₁周边上的点，满足最小。在后一种情况下，搜索空间是整个C₁周边减去a₀到C₁圆心、到C₁圆心两条线段之间的弧，且二分搜索主要用于发现。当计算出后，被更新为与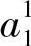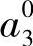，有关的，等。最后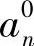，被更新为与，a₀，C_n有关的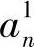。由新点集定义的汇聚节点访问路线长度要比原来短一些。重复进行采取新点集作为输入的迭代更新过程，直至访问路线长度稳定下来。图6-3b说明了这一过程。

传感器存储空间非常有限。它们只能缓冲有限的数据量。假定传感器有不同的数据生成率λ，某些传感器要比其他传感器访问得更为经常些（与其缓冲溢出时间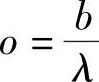有关，其中b是缓冲区大小），以避免数据丢失。参考文献（Gu et al.，2005）研究了缓冲限制条件对于汇聚节点移动性TSP的影响，提出了一种针对汇聚节点移动性的分区调度（Partitioning-based Scheduling，PBS）算法。在PBS中，所有传感器的位置信息都是先验的。传感器被划分为若干组（称为箱子），这样同一箱子B_i内的传感器拥有的缓冲溢出时间变化范围相同，且B_i+1的缓冲溢出时间范围是B_i的两倍。每个箱子又可以根据传感器位置划分为若干个子箱，这样同一子箱内的传感器相互之间的位置靠得非常近。参考文献（Bentley，1975）使用k维数算法实现了这种分区方案。

汇聚节点从B₁子箱中具有最小缓冲溢出时间的传感器开始访问。它沿着所谓的超循环前进。超循环是由许多箱子的访问循环构成的。按照次序，每个访问循环仅包含一个来自于每个B_i箱子的子箱。在每个访问循环中，B_i的子箱后面是位置最近的B_i+1中的子箱。由于B_i+1中的子箱数比B_i多一倍，因而在超循环中，每个B_i的子箱后面会有两个来自于B_i+1的子箱。图6-4给出了包含四个访问循环的超级循环，其中是B_i的一个子箱，每个仅包含一个节点。(www.xing528.com)

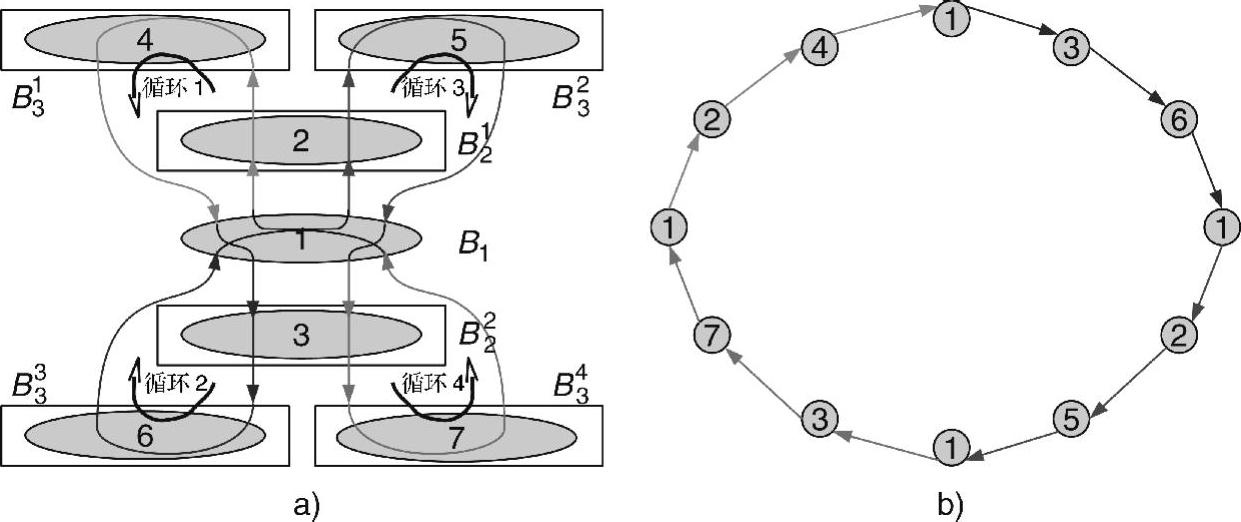
图6-4 四个访问循环组成一个超级循环

a）箱子视图 b）节点视图

在每个子箱中，汇聚节点访问问题可简化为TSP。Prim算法(Prim，1957)可用于计算子箱的最小生成树(MST)，且访问次序由预先安排好的树径确定。需要注意的是，在访问完最后一个子箱后，汇聚节点移向下一个子箱中最近的传感器，而不是返回当前子箱第一个受访传感器。一旦构建完路径，无丢失数据采集所需的汇聚节点最低速率可根据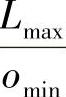来确定，其中L_max是针对传感器的两次连续访问之间的最长路径长度，而o_min是最短缓冲溢出时间。

参考文献(Gu et a1.，2006)研究了区分消息传送问题中的汇聚节点移动性调度。在这种场景下，传输周期性生成的常规消息时，不会出现传感器缓冲溢出的情况，且不定期生成的紧急消息在期限内发送。PBS算法(Gu et al.，2005)提出了一种调度方案，汇聚节点到每个传感器n_i的两次访问之间的间隔不大于有效溢出时问eot(o_i)，该参数与传感器的缓冲溢出时间o_i有关，即传感器n_i所在箱子的最短溢出时间。但是，如果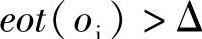，则PBS解决方案无法保证紧急消息及时传送。参考文献(Gu et al.，2006)建议故意缩短一些传感器的eot，并支持多跳消息中继来处理这种情况。它通过一种新算法来实现，将采用PBS(Gu et al.，2005)的多跳路由到移动单元(Multihop Route to Mobile Element，MRME)作为子程序。

在覆盖传感器处，可以满足紧急消息传输期限，即eot≤△处的传感器。在MRME中，未覆盖传感器处生成的紧急消息，不需要等待现场提取。可以将它们中继到d_max（预定值）跳（从发起方起算）内的附近传感器，汇聚节点多次访问过这些传感器。假定t_tr表示每跳传输延迟。如果将传感器n_j处生成的紧急消息发送到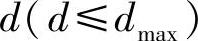跳邻居n_i，然后针对无损调度，汇聚节点到n_i的两次访问之间的间隔最多应当是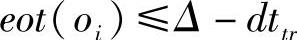。对于覆盖其n_j的n_i来说，汇聚节点访问它的频率至少应当是。

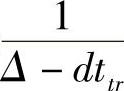对于传感器n_j来说，缓冲溢出时间缩短将导致汇聚节点访问频率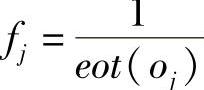增加。将相对增加量定义为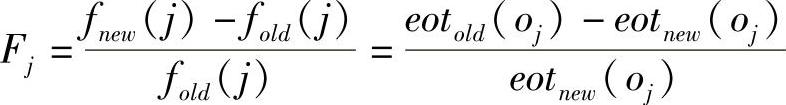。用C(n_i，d)表示n_i的未覆盖d跳邻居。在n_i的d跳区域N_i，d内，由溢出时间减小带来的n_i增益可定义为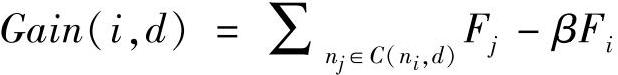，其中β是一个用于调节算法特性的系统参数。在最坏情况下，n_j处生成的紧急消息延迟D_i可表示为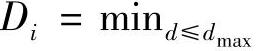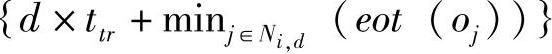。使用上述符号，算法MRME的精髓可以描述如下。

算法MRME的实现分三个阶段。在第一阶段，与PBS一样，传感器被划分为多个子箱，通过检查不等式D_i＞△是否满足来识别未覆盖节点n_i。在第二阶段，一些节点的缓冲溢出时间迭代缩短，直至没有未覆盖传感器存在。在第三阶段，使用修改后的溢出时间来运行PBS，生成一个汇聚节点移动性调度。在第二阶段的每次迭代中，会找到n≤d_max时的Gain（i，d₀），且n_i的缓冲溢出时间缩短为Δ-d₀t_tr。然后，重新计算未覆盖节点集，更新网络中的最短溢出时间o_min。

3.标签覆盖访问的数据采集

参考文献（Sugihara and Gupta，2007；Sugihara and Gupta，2008）研究了针对数据采集延迟最小化的汇聚节点路径选择问题。作者摒弃了从汇聚节点到每个传感器区域只能访问一次的要求。如果相交路径的长度很短，且每个传感器的通信范围很小，则直觉上我们认为汇聚节点的访问时间会长，因为在这种情况下，汇聚节点必须减速以采集所有数据。只访问一次的要求并不总是制胜策略。多次访问与合理的速率控制也可以得到较好的解决方案。

作者通过将搜索空间缩小为一个完全地理图，来简化路径选择问题。在该图中，顶点位于传感器位置和汇聚节点初始位置。假定汇聚节点沿着图中从顶点到顶点的边移动。每条边与一项成本和一个标签集相关联。成本定义为边的欧氏长度，标签集代表一组通信范围与该边相交的传感器，即当汇聚节点沿着边进行访问时，能够从中采集数据的传感器。图6-5给出了这样一个完全地理图，它是由网络中6个传感器构建的。在该图中，传感器的通信范围用虚线表示，同时还给出了入射到节点5上、与链路有关的标签集。

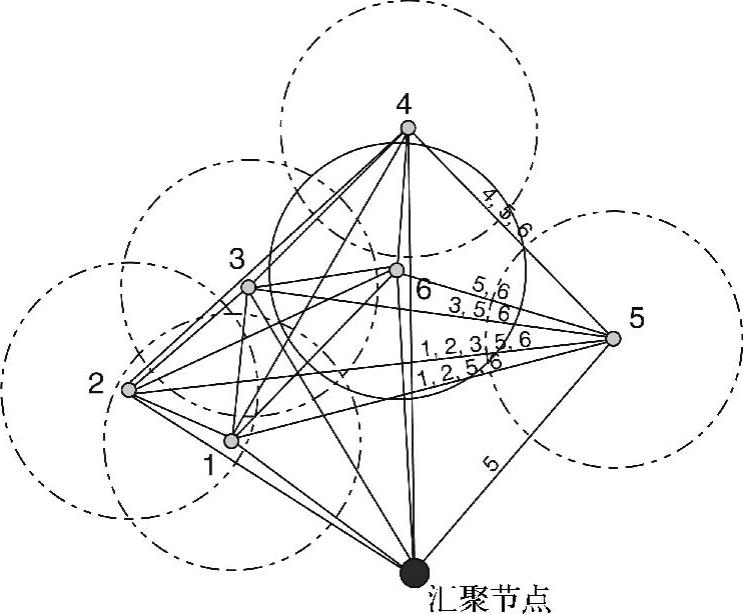
图6-5 传感器与汇聚节点的完全图

目标是找到最低成本访问路径，沿着该路径，汇聚节点可以采集到所有传感器的数据。换句话说，一条最短的访问路径，其相关标签集能够覆盖所有传感器。在这种环境下，汇聚节点不一定访问所有顶点。作者证明最短标签覆盖路径问题是NP难问题，并提出了一种近似算法来解决该问题。算法首先使用任意TSP解决方案，找到了一条TSP访问路线。然后，通过动态编程，通过使用指向T的捷径，得到了最短的标签覆盖路径。采用参考文献（Sugihara and Gupta，2007）中的速率控制算法和作业调度算法，作者用实验验证了算法的有效性，并证明当传感器通信范围较大时，它比类似TSP的算法具有更优的性能。