构建Wi-Fi网络能耗模型——考虑路径能耗最小化

在本节中，我们将基于上面的网络模型和假设，来构建能耗模型。假定n表示网络中的节点总数，A=πR²是网络区域的面积（即C_q的面积）。我们有

n=ρA=ρπR² （6-2）A_i（1≤i≤q）中的预计节点数n_i可表示为

n_i=ρA_i=ρπ（R²_i-R2i-1） （6-3）对于均匀分布的数据源来说，A_i中的预计数据源数T_i为

由于在圆环A_j（j>i）中，与数据源相关的源到汇聚节点路径都将汇聚节点作为目标，A_i作为消息转发者全体参与所有这些路径。在A_i中，每个节点的这些路径预计数m_fw（i）为

在A_i中，每个节点发起的路径预计数m_og（i）为

因此，在A_i中，每个传感器的能耗E（i）为

E（i）=（m_fw（i）+m_og（i））E_c（w_i）根据式（6-1）～式（6-6），我们有

式（6-7）是用于描述传感器能耗行为的通用公式。根据这一公式，我们不难发现E（i）与λ和T成正比，与ρ和R²成反比。当每个传感器是一个源时，即当T=n=ρπR²时，E（i）变得独立于T和ρ。当固定参数λ、T、R和ρ可以忽略时，式（6-7）变为

现在，让我们确定能够实现E（i）（1≤i≤q）最小化的最优w_i值。需要注意的是，w_i值不能大于r_c，否则网络可能被分割。我们分别研究传感器具有固定传输半径和传感器具有可调传输半径的情形。

1.固定传输半径

当传感器有一个固定通信半径r_c时，A_i中的节点传输功耗通常是相同的。在这种情况下，在式（6-7）中，可以用r_c来代替w_i。最优w_i由E（1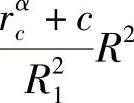）=确定。我们注意到，为了实现E（1）最小化，需要将R₁（即w₁）设置为最大值r_c。利用这个结果，我们能够以递归的形式得出：为了实现E（i）最小化，应当设置R_i=ir_c，w_i=r_c。这样，R=R_q=qr_c。从式（6-8），我们可以得出A_i中每个节点的归一化最佳能耗E_opt（i）

从式（6-9）可以看出，汇聚节点周围存在着不均匀能量消耗现象：传感器距离数据汇聚节点越近，则它能量消耗速率越大，因而电池能量用尽越快。

2.采用不均匀节点分布来平衡能量利用

我们讨论如何恰当使用不同圆环中的不同节点密度来平衡能量消耗。假定圆环A_i中的节点密度为ρ_i。显而易见，为了平衡能量利用，靠近汇聚节点的圆环应当比相对较远的圆环包含更多节点，来共同承担消息中继负荷，即ρ_q＜ρ_q-1＜…＜ρ₁。我们的目标是确定ρ_i是ρ_q的一个函数，它满足E_opt（i）=E_opt（q），其中1≤i≤q，q=R/r_c。

将式（6-7）中的ρ用ρ_i代替。需要注意的是，E_rate（i）现在也与ρ_i有关。通过类似的讨论，我们可以得到A_i中每个节点归一化最优能耗E_opt（i）

由E_opt（i）=E_opt（q），我们得到

对上式进行简单的演算，可以得到ρ_i，它是ρ_q的函数

3.可变传输半径(www.xing528.com)

现在，我们假定每个传感器能够调整其传输半径，最大可以达到r_c。假定理想情况下，传感器能够沿着从源到汇聚节点的直线转发数据，传输半径与圆环宽度对应。因此，路由能耗为

根据上式，当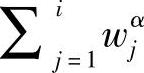最小时，E_path（i）最小。定义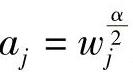，1≤j≤i。于是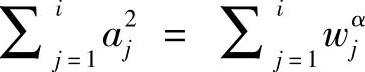，。根据拉格朗日恒等式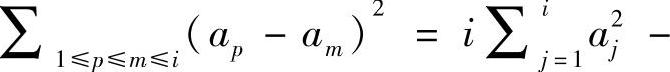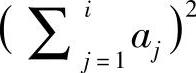，。因此

我们证明，通过分别考虑表达式的右边各项，并确保对于同一值来说，两项全都最小，这样可以实现仅当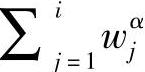最小化。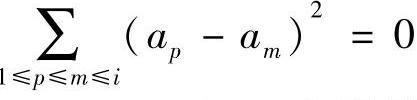显然是最小值，当知，功率平均函数且仅当a_q=a_q-1=…=a₁，即w_q=w_q-1=…=w₁=R₁。众所周知，功率平均函数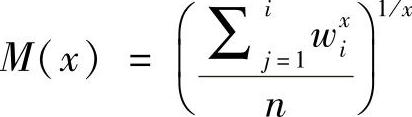是非减函数。在x取特定值x=α/2和x=1时，应用该函数。当x=1时，函数值为常数（因为圆环宽度之和固定的），而x=α/2时，对于w₁=w₂=…=w_q来说，函数值为常数。需要注意的是，参考文献（Olariu and Stojmenovic，2006）最初给出的证明并未实现两种和最小化，因而仍然是不完整的。于是

R_i=iR₁

我们看到，确定R₁是关键。根据式（6-8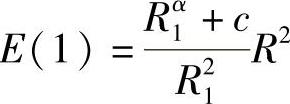），。当α=2，R₁=r_c时，E（1）最小。现在，我们研究α＞2的情况。给定α和c，当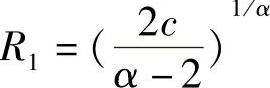时，E（1）最小（当这个函数的导数等于0时，可以得出该值）。由于传感器传输半径上限为r_c，因而我们有

需要注意的是，R₁最佳值与网络区域的半径R无关。

用iR₁来替代式（6-8）中的R_i，我们得到A_i中某个节点每条路由的归一化能耗

这是与式（6-9）相同的表达式。每条路径能耗最小化会导致汇聚节点周围较大的能量消耗。

4.通过调整传输半径来平衡能量利用

我们将描述在半径为R的整个圆盘上，如何通过调整圆环宽度，来支持传感器具有相同能量消耗速率（从而平衡能量利用）。显而易见，对于具有统一能量消耗速率的传感器来说，靠近汇聚节点的圆环（其消息中继负荷任务重）宽度要比相对较远的圆环窄，不等式w₁<w₂＜…＜w_q必须成立，以降低传感器在进行跨圆环传输时的能量利用。我们的目标是确定最优w₁（即R₁），然后计算作为w₁函数的w_i，使得E（i）=E（1）。

最优值R₁由式（6-14）确定。根据E（i）=E（1），我们有

通过简单的代换，上面的方程可以写成

我们得到如下等式

注意到a_i-1仅与R_i-1有关。因此，一旦R_i-1已知，我们可以使用式（6-16）来计算w_i。由于根据R_i-1=w_i-1+R_i-2可立即确定R_i-1，因而可以通过迭代方式来计算w_i。也就是说，w_i是R₁的函数。我们还有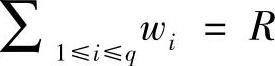。因此，在迭代过程中，当达到总宽度R时，q值也可以确定下来。

对于α=2来说，无法实现能量利用平衡（E（1）=E（2）=…=E（q）），不管R、r_c和c如何取值。关于这种负面结果推导的详细信息，见参考文献（Olariu and Stojmenovic，2006）。

需要注意的是，这里采用可调传输半径来平衡能量消耗时，假定每一跳长度与对应圆环的宽度w_i相同。这种路由与沿着直线的路由相对应，且在预期位置传感器是可用的。当然，为了利用这一假设，高密度的传感器是必要的，但即使是这样，可能也无法满足能量平衡的要求。参考文献（Olariu and Stojmenovic，2006）实际上无法设计一个基于理论研究成果、合理平衡能量的数据采集方案。因此，这仍然是一个悬而未决的问题。