Gabriel图路由优化方案

平面图要正常工作，需要GG充当面路由。面路由性能存在的主要问题是需要用到面边缘的绝大部分。因此，参考文献（Bose et al.，1999）提出了一种面路由与基于距离的贪婪路由的组合。该算法称为GFG（贪婪-面-贪婪），应用贪婪算法直至数据包到达某个节点，使得所有该节点的邻居比节点本身距离目标节点更远。应用面路由直至数据包到达另一个节点，该节点距离目标更近。然后，继续使用贪婪路由算法。该算法可以在贪婪路由和面路由模式之间进行多次切换，但由于面路由通常非常成功，因而能够保证进度和数据传输，且由于算法通常以贪婪模式推进，因而不会形成环路，而面路由模式也能确保在推进过程中不形成环路（即它能够确保恢复过程的正常进行）。

图4-9所示的实例说明了面路由如何在空穴区进行路由。假定采用贪婪算法，数据包到达节点S，该节点比其他邻居更靠近目标D。恢复过程需要用到面路由，即找到一个比S更靠近D的节点。如果采用右手定则，则数据包沿着最短路由直至到达第一个节点B，该节点比S更靠近D。同样，如果采用左手定则，则数据包沿着更长路由到达节点C。恢复过程结束后，继续使用贪婪算法。

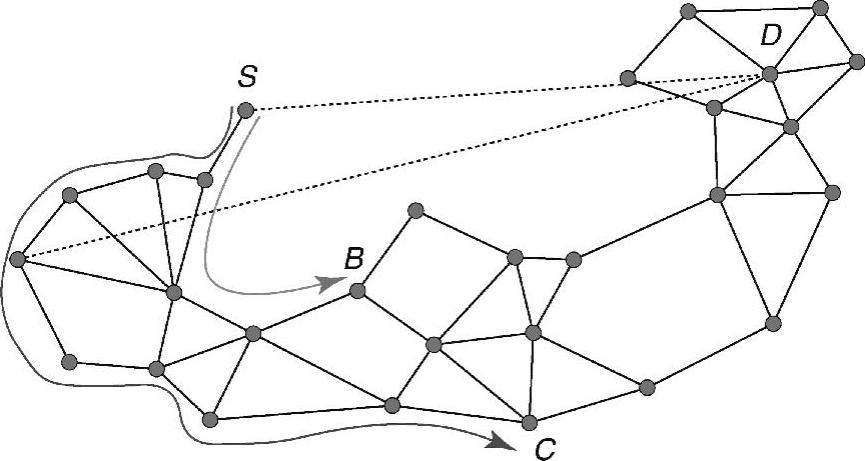
图4-9 遍历面直至恢复过程启动

GFG算法如图4-10所示，从源节点S到目标节点D。粗边属于GG，所有边属于UDG。由于S无法发现比自己更靠近D的任何邻居，因而首先应用面路由。假定采用左手定则，数据包沿着路由SYXTPOK前进，直至到达第一个节点K，它满足|KD|＜|SD|。然后，采用贪婪算法，数据包沿着路由KGHI前进，直至到达节点I，该节点不存在比自己更靠近D的任何邻居。于是，再次应用面路由，数据包沿着路由IHGFECB前进，直至到达节点B，它满足|BD|＜|ID|。需要注意的是，面路由仅考虑了GG中的边，并没有选择边BE。然后，采用贪婪算法，数据包最后经由路由BAD到达D。如果采用右手定则，则数据包沿着路由S→Z→S→Y→X→W→V→W→U→T→R→T→P→Q→P→O→M→N→M→L→J→F前进，到达第一个节点F，它满足|FD|＜|SD|。然后，采用贪婪算法，数据包沿着路由FEBAD前进（在贪婪路由算法中，选择了边BE），直至最终到达目标D。

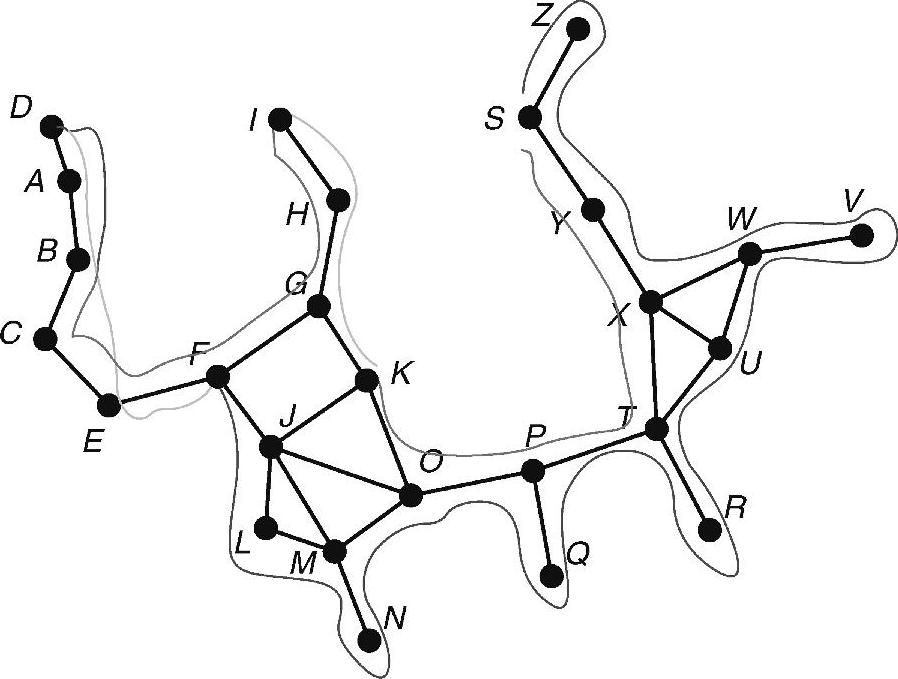
图4-10 采用左手和右手恢复实现的从S到D的贪婪-面-贪婪路由

如果源节点与目标节点是断开的，则GFG将形成一个环路。如果面路由中的第一个边在遍历过程中沿同一方向重复了两次，则检测到环路存在。第一个边可添加到消息中，这样如果它出现重复，将会被检测到。需要注意的是，不是路径上任何节点出现重复都可以推出存在环路。

采用GG作为平面图的GFG变形具有比采用RNG的面路由变形更少的平均跳数，因为GG比RNG更密集（RNG是GG的一个子集），因而具有更多边。边越多会导致面上的边越少，因而跳数也就越少。

参考文献（Datta et al.，2002）对GFG算法进行了改进，进一步降低了平均跳数。每个转发节点使用局部可用的两跳信息，来计算尽可能多跳的信息，并将消息转发给下一个已知跳，而不是将它转发给下一跳。采用CDS技术，除了第一跳和最后一跳外，面路由可以在支配集上执行。

增加了802.11媒体接入层的GFG能够以贪婪周边无状态路由（Greedy Perime-ter Stateless Routing，GPSR）协议的形式实现（Karp and Kung，2000）。GPSR协议是GFG的一个变形。更准确地说，GPSR使用前交叉而不是后交叉变形，它使用RNG来替代GG。但是，这些修改并未改善路由协议的性能。参考文献（Kim et al.，2005）指出，GPSR无法保证任意平面图中的数据包传输。参考文献（Frey and Stojmenovic，2006）证明了这一事实，并进一步给出了任意平面图GFG传输保证的正式证明。这主要是由于GFG和GPSR之间的面路由过程存在差异导致。通常情况下，当算法中的线段XD与其他线段相交时，GPSR将会切换到其他面。但是，GFG正确选择合适的面，一旦交点确定，该面相交前后有时不会发生改变，参见图4-6。有意思的是，当GG用作平面图时，通常不会发生面切换，这就是GPSR实现中的错误在参考文献（Frey and Stojmenovic，2006）提出之前，未被发现的原因。更多关于GFG和GPSR区别的信息可阅读参考文献（Frey and Stojm-enovic，2006）。下面的定理表明，在GG中，当从贪婪路由失败中开始恢复时，到达比当前节点更靠近目标的节点通常是可行的。因此，在使用面路由遍历完某个面后，可以继续使用贪婪路由算法。

定理4-3 （Frey and Stojmenovic，2006）：假定SD是Gabriel图G中源节点与目标节点D之间的线段。对于GG中与线段SD相交的任意边UV来说，D和至少一个边端点U或V之间的距离小于S和D之间的距离。

证明：由于UV位于GG中，直径为|UV|的圆无法包含节点S和D。这样，∠USV和∠UTV都小于90°（如图4-11所示）。由于四边形SUDV角度数之和为360°，∠SUD和∠SVD中至少有一个角应当大于90°。这使得SD成为对应三角形中最长的边。因此，两个节点U和V中，至少有一个节点比节点S更靠近D。

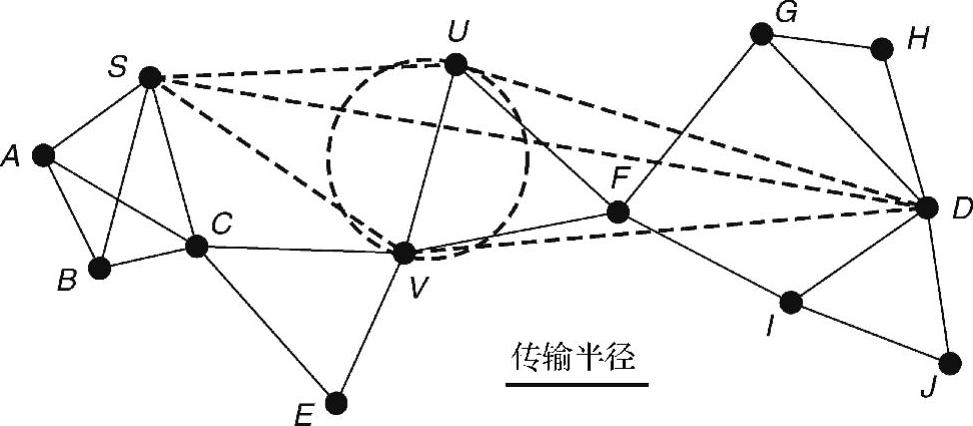
图4-11 通常情况下，GG中的面路由可以找到一个距离目标更近的节点(https://www.xing528.com)

（所有实线边都属于GG）

因此，使用GG的GFG可以通过如下简单算法来实现。GFG over GG（Frey and Stojmenovic，2006）

重复

采用贪婪路由算法直至节点S数据包转发或出现失败

if节点S处出现失败，then

选择包含线段SD的面f

遍历f直至采用贪婪路由算法成为可能

endif

until数据转发

参考文献（Kuhn et al.，2003a）提出了一种称为贪婪其他自适应面路由加（Greedy Other Adaptive Face Routing Plus，GOAFR+）的GFG扩展算法。它发现面路由的效率取决于面遍历的方向。对于某个面来说，如果选择了不合适的方向，则会导致指向目标的路径变长。因此，GOAFR+的基本思路是引入一个圆心位于目标节点的圆C，其初始半径设置时将源节点包含在内。一旦存在更靠近目标的下一跳节点，则采用贪婪模式。只要当前受访节点位于圆C内，圆C的半径就呈指数规律减小。一旦贪婪模式到达一个凹节点U，则会触发面路由的修正版。如果在没有接触圆C的前提下，面已经完成了遍历，则数据包将被改善给当前的受访节点，它比U更靠近目标（如果没有节点比U更靠近目标，则报告路由失败）。如果首次接触圆C，则反方向对面进行遍历。如果第二次接触圆C，且不存在比U更近的受访节点，则面遍历继续从U开始，且C的半径呈指数规律减小。一旦面遍历达到预定常数，且出现了更多靠近目标的节点，则GOAFR+中断面遍历，再次切换到贪婪模式。

路径成本被定义为路径中所有边的成本之和，此处的边成本可能会有任意度量标准，它是欧氏距离的多项式。参考文献（Kuhn et al.，2002）表明，最坏情况下的任意几何路由算法的成本至多受到二次路径成本的限制（与加权最短路径相比），二次路径成本可用渐近最优性来表示。参考文献（Kuhn et al.，2002）指出，当连接凹节点的线段与目标首次相交时，如果面遍历切换回贪婪模式，则无法实现渐近最优性（如GFG不是渐近最优的）。当数据包遍历整个面，并在最靠近目标的面边缘切换回贪婪模式时，则贪婪路由和面路由的组合是渐近最优的。参考文献（Kuhn et al.，2003b）证明，虽然GOAFR+通常情况下无法遍历整个面，但它仍是渐近最优的。

确保传输的地理路由面临着重大挑战，上千篇学术论文都提到了这一点。对于确保传输的地理路由来说，不准确的位置信息是一个重大问题。在3D地理路由中，不存在具有保证传输特性的局部无记忆算法。GG要保持连通状态，要求单位圆盘图的传输半径相同，且不存在障碍物。参考文献（Barriere et al.，2001）给出了模糊UDG的一种扩展形式。如果两个节点的距离小于r，则这两个节点处于连通状态；如果两个节点的距离大于R，则这两个节点处于断开状态。如果满足R/r＜1.41，则主算法生效，它包含有用于维护GG所需的特定扩展和消息开销。对于其他成本度量标准，仍然不存在恢复模式下基于GG的面路由的真正替代方案，该面路由主要用于选择靠近目标节点的邻居。现有的改进方案通常基于面遍历边上的捷径、支配集、最短加权路径。

另一个挑战是与路由过程中路由上中间节点之间移动性有关的问题。该算法是一种针对静态网络的无环路算法，但移动节点可以形成环路。进入到某个面之后，同一面上的两个节点可以通过移动互相靠近，并将面划分为两个新面，在其中的一个新面处留下一条不与从源到目标的假想线相交的消息，这样就形成永久性环路。但是，该问题可通过添加最后一次与假想线SD相交的时戳并忽略之后生成的链路来部分解决（如果移动性尚未高到无法获取所需信息的程度）。