平面几何图中的面路由策略

平面图是指可以画在平面上，且各边仅在其端点相交的图。图4-6给出了一张平面图。在几何图中，每个节点都知道自己及其邻居的位置，因而也知道与邻居连线的角度。平面和几何图的实例包括街道地图、建筑物内同一层楼的房间等。平面几何图将图分成多个面。在图4-6的实例中，面F₁是多边形SABC，而F₂是多边形BEFGHC。参考文献（Kranakis et al.，1999）描述了针对平面几何图的第一个无记忆局部路由算法，它能够在源节点和目标节点建立连接的任何时候确保传输质量。

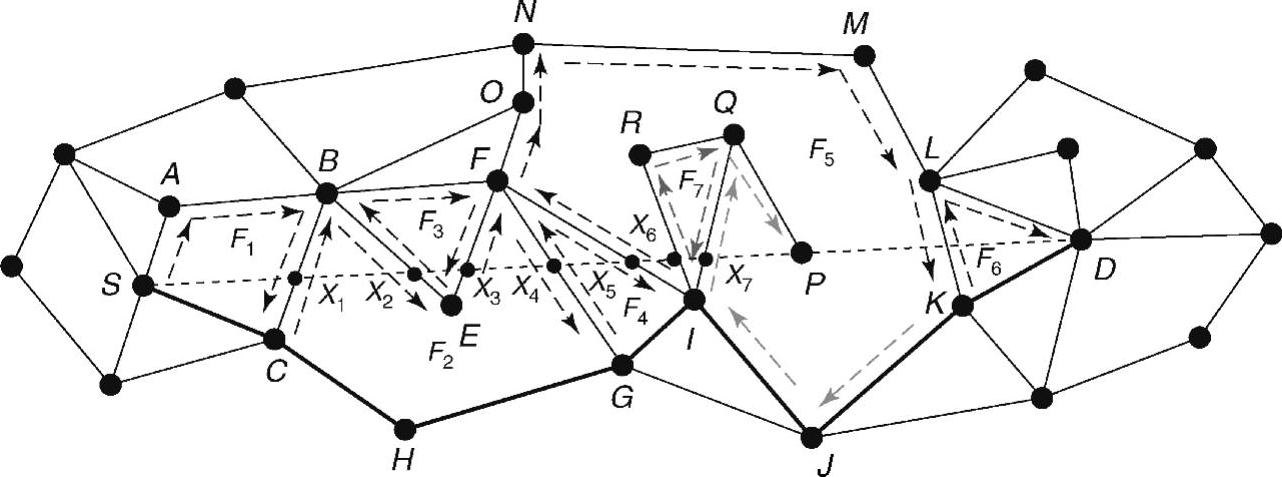
图4-6 面路由

参考文献（Bose et al.，1999）提出的面路由，是对参考文献（Kranakis et al.，1999）中路由算法的一种改进方案。面路由（Bose et al.，1999）的主要思路是，使用包含连接上一个交点X（最初的交点是源节点S）和目标节点D的直线线段的面交点，不断将交点向前推进（指向目标节点D）。数据包沿着面的内部进行路由，直至路由上的某个边与连接X和D的线段XD相交。在图4-6中，线与平面图相交于F₁，F₂，…，F₇。通过使用右手定则（逆时针遍历）或左手定则（顺时针遍历），来遍历任意面的边缘。在右手定则中，将右手放在墙壁上，然后向前走，即可遍历面。也就是说，数据包沿着下一个边进行转发，下一个边可以通过数据包已到达的边逆时针旋转得到。当数据包到达与线段XD相交的边时，下一个与该线段相交的面以同样的方式进行处理。该过程持续进行，直至数据包到达目标D，或者当前面遍历的第一个边在同一方向上被遍历了两次（这种情况表明源节点和目标节点是断开的，形成了环路）。

考虑图4-6中给出的实例，假定采用左手定则。面F₁与线段SD相交，数据包沿着路径SABC在F₁中进行遍历，直至BC与线段SD在X₁处相交。下一个面F₂沿着路径CBE进行遍历，直至下一个交点X₂出现，然后面F₃沿着路径EBFE进行遍历，直至交点X₃出现。然后路径再沿着EFG在面F₂上进行遍历，数据包在面F₄上沿着路径GFI进行遍历，在面F₅上沿着路径IFONMLK进行遍历，最后在面F₆上进行遍历，直至将数据包转发给D。整个路径使用虚线表示。通常情况下，该变形可以来回遍历所有相交的边，又称为后交叉变形，在每个面上，同样可以使用右手定则。如果我们想避免边两次相交，可以采用前交叉变形。它也可以首先使用左手或右手定则，或基于其他标准选择一个方案，例如使用指向目标节点D的最小初始角/方向。数据包可以沿着边SC对面F₁进行遍历，该边比SA在方向上更接近于SD。选择下一个面F₂，参考线变为X₁D。数据包从C转发到H，然后转发到G，直至边GF与线段X₁D相交于点X₄。同样，面切换到F₄，数据包从G转发至I，边IF与线段X₄D相交于点X₅。最后，数据包经由粗线表示的路径SCHGJKD到达D。

需要注意的是，相交后的遍历面可能与XD相关前的遍历面相同。假定目标节点是图4-6中线段SD上的点P，且采用后交叉变形（虚线）。在遍历F₅的点K时，路径将继续沿着KJIQ在F₅上运动。在IQ和SP的交点X₇处，面F₅再次被选中，且采用算法（Bose et al.，1999）进行遍历，由于它包含线段X₇P，且在后交叉或左手变形中，消息沿着路径IQP传送到P；在前交叉或右手变形中，消息沿着路径X₇JKLMNOFX₇RQP传送到P（图中未标示）。但是，算法（Karp and Kung，2000）迫使面在每个相交边X_iD处发生变化（需要注意的是，X_i必须是线段X_i-1D上的内点）。然后，算法（Karp and Kung，2000）选择面F₇，消息沿着QIR或IRQ在环路中不停地进行遍历，因为X₆没有位于线段X₇P内。面变化将永远不再发生，从而形成一个环路。因此，该步骤在参考文献（Bose et al.，1999）中得以准确实现，但在参考文献（Karp and Kung，2000）出现描述性错误，导致在任意平面几何图中缺少传输保证。

目前，存在着多个面路由的变形，主要是在每个遍历面上，采用左手或右手定则来解决各种决策问题。当沿着路由与某个边交叉前或交叉后，面就会发生变化，导致差异产生。面算法的少数变形可描述如下：

面路由

//S：源节点；D：目标节点

涉及(www.xing528.com)

X←S

重复

假定f为G的面，X位于其边界上，且与线段XD相交

顺时针（逆时针）遍历f直至到达边UV

边UV与线段（X，D）在某个内点Q≠X处相交

X←Q

继续从节点U（与XD交叉前）或节点V（与XD交叉后）处开始寻找路由

直至X=D。