基于投影和方向的贪婪路由优化策略

地理路由最简单的形式是贪婪路由，参考文献（Finn，1987）最早对它进行了描述。在贪婪路由算法中，路由中的每个节点将数据包转发给邻居集合中最靠近目标节点的邻居。这样，只有比当前节点更加靠近目标节点的邻居才会列入考虑范围。算法如图4-1所示。假设节点S路由中的当前节点，而节点D为目标节点。节点S的所有邻居都位于圆心为S的圆内。

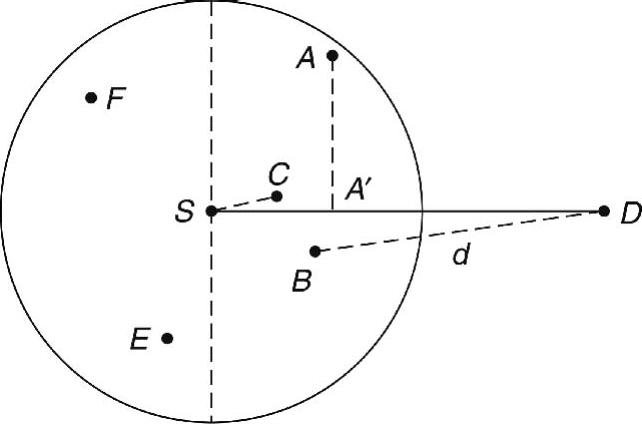
图4-1 基于投影和方向的贪婪路由

假设在S的所有邻居中，节点B是最靠近目标节点D的邻居，d为B和D之间的距离。根据贪婪路由算法，节点S选择节点B作为下一跳转发节点。贪婪路由适用于高密度、大规模网络，且由于贪婪路由具有简单化、局部化的特点，因而拓扑结构不断发生变化。在每跳路由中，与目标节点的距离都实现了最小化。GEDIR（Stojmenovic and Lin，2001a）算法是贪婪路由的一种变形。该算法将所有邻居（甚至是后向的邻居）考虑在内，并选择最接近目标的节点。如果某条消息将被回送到发送它的节点处，则删除该消息。另一种算法是在更接近目标的当前节点中，选择最靠近目标的节点。该算法称为最接近（Nearest Closer，NC）方法，是由参考文献（Stojmenovic and Lin，2001b）提出的。

参考文献（Takagi and Kleinrock，1984）对第一个地理路由进行了描述。该文献引入了进度的概念，用来定义半径内的最大转发（Most Forward within Radius，MFR）贪婪路由算法。假设A是S的一个邻居，从A到D的进度对应于两个向量SD和SA的点积SA·SD=∣SA′∣∣SD∣，其中SA′是SA在直线SD上的映射，∣XY∣表示X和Y之间的欧氏距离（参考文献（Stojmenovic and Lin，2001a）给出了进度的点积公式）。MFR算法考虑了S的所有邻居，并选择节点A，使得SA·SD最大化。也就是说，映射SA′的（带符号的）长度实现了最大化。这样，节点S将分级转发给节点A。MFR算法仅考虑那些具有合适进度的邻居。具有转发进度的最近邻居（NFP）算法（Hou and Li，1986）在所有正进度中，选择距离目标最近的邻居。

地理路由的另一个策略是使用下一跳候选节点与目标节点连线有关的方向信息。Kranakis、Singh和Urrutia在参考文献（Kranakis et al.，1999）中提出了指南针路由（也称为DIR方法）。它根据与候选邻居A和目标节点D相连的直线之间的夹角∠ASD最小化原则，来选择下一跳。在图4-1的实例中，∠CSD是所有S邻居中夹角最小的，因而选择节点C作为转发节点。

参考文献（Stojmenovic and Lin，2001a）证明，贪婪、GEDIR和MFR路由是无环路的，而DIR是有环路的。贪婪路由选择比当前节点更靠近目标节点的邻居。由于不存在回溯，因而它是无环路的。MFR是无环路的证明如下：假定A₁，A₂，…，A_n是环路中的节点，且A₁向A₂转发数据包，A₂向A₃转发数据包，……A_n-1向A_n转发数据包，A_n向A₁转发数据包。在当前节点S处，由于AD·SD最小（即SA·SD最大），因而MFR选择邻居A作为转发节点。由于A₁向A₂，而不是向A_n转发数据包，因而有DA_n·DA₁＜DA₂·DA₁=DA₁·DA₂。同样，我们可以得出DA₁·DA₂＜DA₂·DA₃＜…＜DA_n-1·DA_n＜DA_n·DA₁。它与DA_n·DA₁＜DA₂·DA₁=DA₁·DA₂矛盾。因此，MFR路由是无环路的。

图4-2所示的实例表明，基于方向的路由无法保证UDG中的路由是无环路的。假设S为源节点，B不是它的邻居（传输半径如图所示）。根据基于方向的路由，由于A偏离线段SD的程度小于C，因而节点S选择邻居A作为转发节点。同样，节点A选择B，B选择C，C选择S。这样，基于方向的路由形成环路S→A→B→C→S。(www.xing528.com)

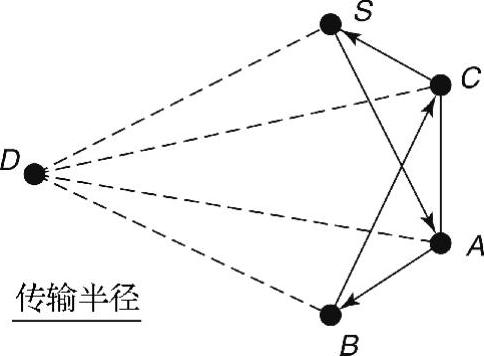
图4-2 基于方向路由的一个反例

图4-3所示为5种路由算法的描述：贪婪、MFR、DIR（指南针）、最短路径（跳数方面）和NC路由。任务是发现从源节点S到目标节点D的一条路由。

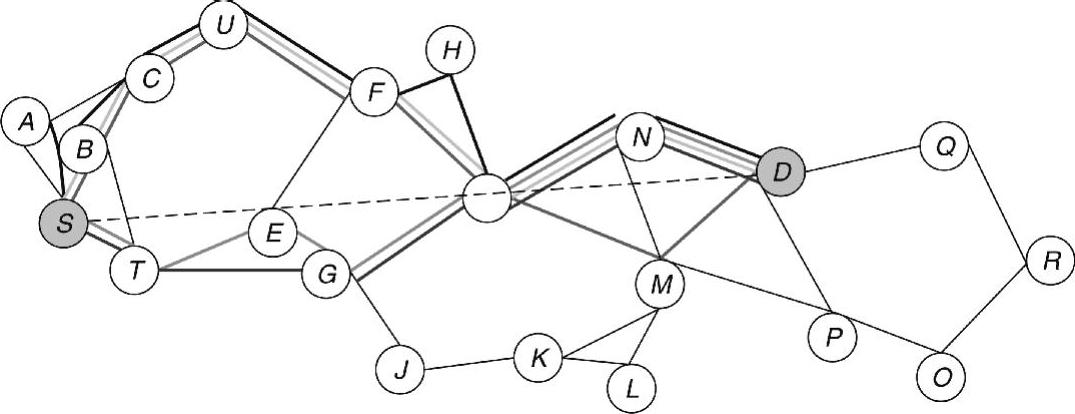
图4-3 使用不同路由算法得到的路径

（贪婪路由算法S→C→U→F→I→N→D；MFR路由算法：S→C→U→F→I→M→D；DIR路由算法：S→T→E→G→I→N→D；最短路径路由算法：S→T→G→I→N→D；NC路由算法：S→B→C→U→F→H→I→N→D）