区域覆盖算法中的覆盖与连通性标准

通过提供计算高效的构成因子，覆盖与连通性标准可作为区域覆盖算法中的组成部分。标准的选择取决于感知半径（SR）和传输半径比值及其均匀度。

如果感知半径（SR）和传输半径相等，则覆盖特性可通过验证感知圆的整个周长是否被其他圆所覆盖来进行检验。在图3-2a所示的实例中，节点O的感知区域未被其他两个圆完全覆盖。标准的正确性可以从如下观测结果推出：如果两个感知圆相交，则每个中心位于其他圆内。如果圆O周长上的点A被圆心在P的圆所覆盖，则从点A到圆心线段上的所有点也被同一圆所覆盖，因为点O和A位于圆心在P的圆内，且任一圆的感知区域是凸的。因此，不需要对整个线段OA是否包含在另一个圆内进行检验，而只需要对位于圆周长上的端点A进行检查。需要注意的是，该标准（及如下标准）假定同一位置不会配置两个传感器。

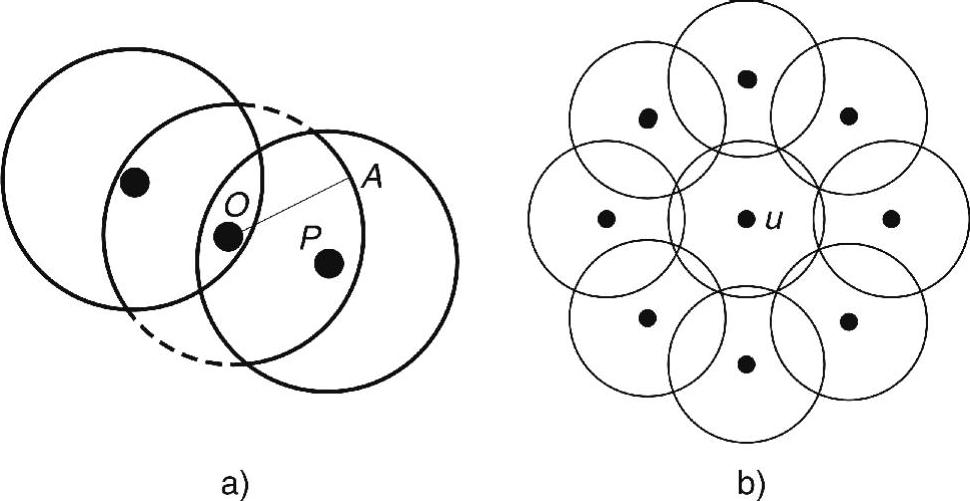
图3-2 基于周长的覆盖检验

该标准可以推广至k-覆盖的情形。当且仅当每个传感器的周长至少被k个不同传感器所覆盖，则称监测区域是k-覆盖的（Huang and Tseng，2003）。如果CR大于SR，则该标准不再适用。在图3-2b所示的实例（k=1）中，假定所有节点都位于节点u的通信半径（CR）内。虽然圆u的周长被其他圆所覆盖，但是节点u的感知区域并未被完全覆盖。

参考文献（Wang et al.，2003和Zhang and Hou，2005）引入了一种覆盖标准，用于确定某个感知区域是否完全被其他感知区域所覆盖。它不要求节点的感知半径相同。同时，该标准不依赖于CR与SR的比值。它可以推广至任意形状（不仅仅是圆盘形）的感知区域，并可应用于对应的边界。

定理3-1 中心位于点O的圆被中心位于点C₁，…，C_m覆盖的问题，可以简化为两个覆盖圆C_i和C_j的交点覆盖问题，或者点O和一个位于点O感知区域内的覆盖圆C_i的覆盖问题，结论如下：如果至少存在两个覆盖圆，且任一交点被不同覆盖圆C_k所覆盖，则感知区域被完全覆盖。

证明：证明的基本思路（见参考文献（Gallais et al.，2008））如图3-3a所示。假定存在一个点P，它未被区域内的任何传感器所覆盖。点P位于一个未覆盖块内，该块边界是由一系列感知圆的外弧和感知区域边界确定的。在图3-3a中，未覆盖块是阴影区域Q-R-S-T-U。从点P移动（沿着任何方向）到未覆盖块的边界，并沿着边界移动，直至到达边界上的某个交点，如图3-3a中两个覆盖圆C和D的交点Q，或者覆盖圆D和中心圆O的交点U。点Q未被任何第三个覆盖圆所覆盖。这与定理的假设条件相矛盾。

由于灰色区域内任意两个圆的交点都被第三个圆所覆盖，因而图3-3b中的中心灰色圆被完全覆盖。例如，圆A和圆C的交换P被圆B所覆盖，圆A和圆D的交点T被圆C所覆盖。

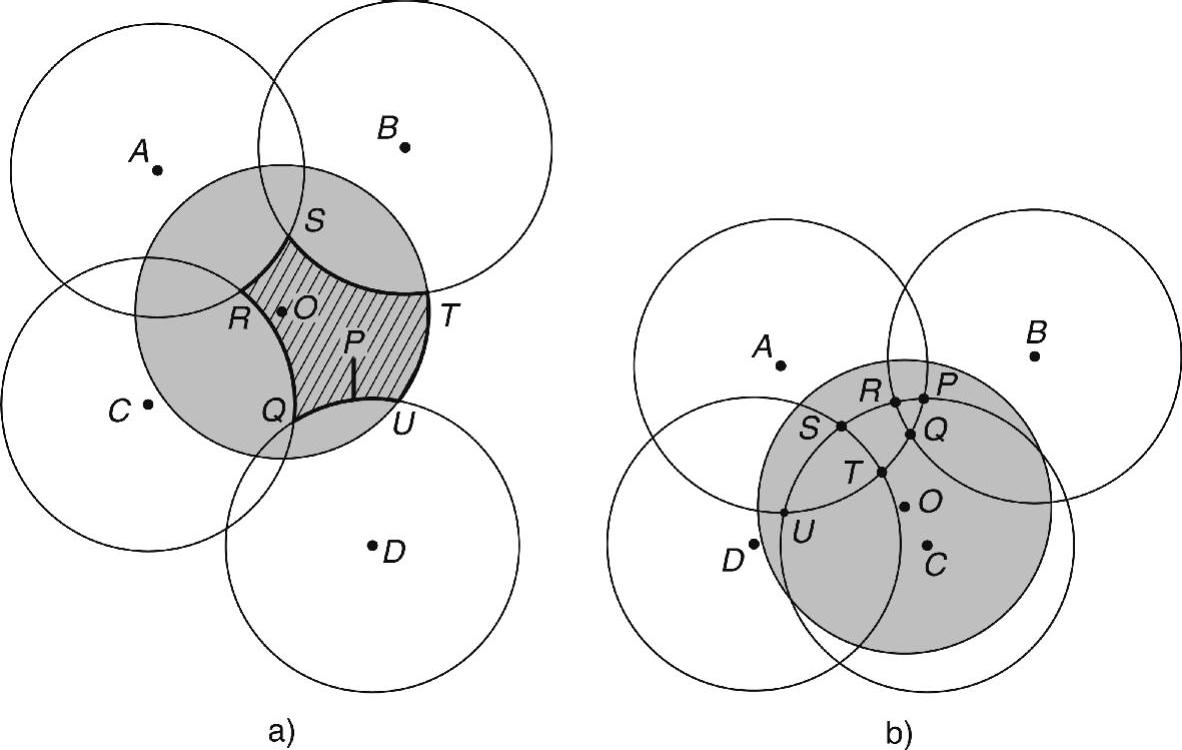
图3-3 如果所有交点被覆盖，则灰色圆被完全覆盖

定理3-1中的标准提供了一种高效的感知区域完全覆盖检测方法。但是，如果该区域未被完全覆盖，则它无法提供与未覆盖区域可能规模有关的直接信息。一种可能的估计方法是随机产生一定数量的点，并检测每个点被现有圆覆盖的情况。未覆盖区域可依据未覆盖点的百分比进行估计。另一种估计方法是基于具有相同顶点的多边形（如图3-3a中的多边形QRSTU），对未覆盖区域进行估计。这就要求设计更为准确的、快速覆盖的规模估算协议。(www.xing528.com)

定理3-1可以扩展至三维（Three Dimension，3D）场景。在参考文献（Ovalle-Martinez et al.，2006）中，该定理可用于3D空间广播协议。在3D空间内，每个节点的传输半径相同。它与传感器体积覆盖场景相对应，此时CR=SR（详细内容见第2章）。在这种情形中，覆盖标准可表述如下：

定理3-2 参考文献（Ovalle-Martinez et al.，2006）：假定球A与球C₁，C₂，…，C_m相交。我们考虑球心位于A、C_i和C_j的球3D周长上的所有交点X。如果至少存在一个这样的交点，且每个交点X至少位于一个剩余球内（对于某个k来说，球心位于C_k），则球心位于C的球完全被球心位于C₁，C₂，…，C_m的球覆盖。在CR/SR比值任意和任意形状的感知体积（为简单起见，本标准仅研究球的体积）的情况下，下面的推广结论成立。同时，假定同一位置不会配置两个传感器。

定理3-3 假定球A与球C₁，C₂，…，C_m相交。我们考虑球心为C_i、C_j和C_k（或C_i、C_j和A）的球的所有位于球A内的交点X。如果至少存在至少一个这样的交点，且每个交点X位于至少一个剩余球内（对于某个p来说，球心位于C_p），则球心位于A的球完全被球心位于C₁，C₂，…，C_m的球覆盖。

证明：定理3-3的证明过程与定理3-1类似。假定球心位于A的体积未被其他体积完全覆盖。假定P是一个未覆盖节点。它位于某个3D未覆盖块内。从点P处开始“移动”，直至到达某个边界。它既可能是某个覆盖圆的边界，又可能是球A的边界。再穿过边界，直至两个球的交线。穿过该交线，直至到达与第三个球的交点。该点未被任何其他球所覆盖（该点不在任何其他球内部），这与定理中的假设条件相矛盾。

参考文献（Zhang and Hou，2005；Wang et al.，2003）对覆盖和连通性标准都进行了研究。结果表明，如果通信半径至少是SR的两倍，且被覆盖区域是凸的，则区域覆盖也意味着覆盖传感器的连通性。这样，参考文献（Tian，2004）通过去除凸条件，对证明进行了推广，根据证明结果，任意两个感知圆相交的节点将成为邻居。

定理3-4 如果通信半径至少是SR的两倍，则区域覆盖也意味着覆盖传感器的连通性。

证明：参考文献（Tian，2004）中的证明过程如下：如果网络是不连通的，则网络中至少存在两个连通分支网络。从两个连通分支网络分别选择的任意一对节点之间的距离大于CR。由于CR>2SR，则两个分支网络中节点的覆盖区域之间不相交。因此，整个区域不是完全覆盖的，因为该区域是连续的（Tian，2004）。

参考文献（Wang et al.，2003）进一步研究了覆盖度和连通度之间的关系。当将任意k-1顶点从某个图中删除时，如果该图仍处于连通状态，则称该图是k-连通的。

定理3-5 参考文献（Wang et al.，2003）：如果通信半径至少是感知半径的两倍（CR>2SR），则一组k-覆盖某个凸区域的节点形成一个k-连通通信图。

参考文献（Simplot-Ryl et al.，2005）对几种集中式传感器区域覆盖算法进行了综述。由于集中式算法信息收集效率不高，导致通信开销过大，因而仅适用于小型网络。我们在这里将仅讨论局部算法。所提出的算法都假定每个传感器知道其位置（地理坐标）。