RNG与LMST的分析介绍，

下一节将要讨论的最小能量广播是基于某些几何结构的。本节将对这些结构进行描述。假定大家已经基本熟悉与最小生成树（MST）有关的知识。对于包含n个节点的加权图来说，其最小生成树是一个将这n个节点作为顶点的最小连通图。最小生成树是一种树形结构，否则在任意圆中，在不影响连通性的情况下，可以将最长的边从图中去除。参考文献（Kruskal，1956）提出的Kruskal算法采用该观测结果来构建MST。所有边按照升序排列，且考虑将其依次按序包含在MST中。在已经构建的MST部分中，如果候选边无法生成一个圆，则它不包含在MST中。

相对邻域图（Relative Neighborhood Graph，RNG）和局部最小生成树（Local-ized Minimal Spanning Tree，LMST）是两种在各类拓扑构建中使用的著名平面图。平面图是一种在平面上以特定方式画出的图，图中各边仅在边的端点相交。图2-19所示为RNG和LMST的实例，同时也图解了平面图。所有非虚线边形成RNG，而所有粗线边形成LMST。虚线边是UDG中的剩余边。边（1，4）属于RNG，但它不属于LMST，因为该边不在节点1单跳子图的MST中（后面将进行解释）。

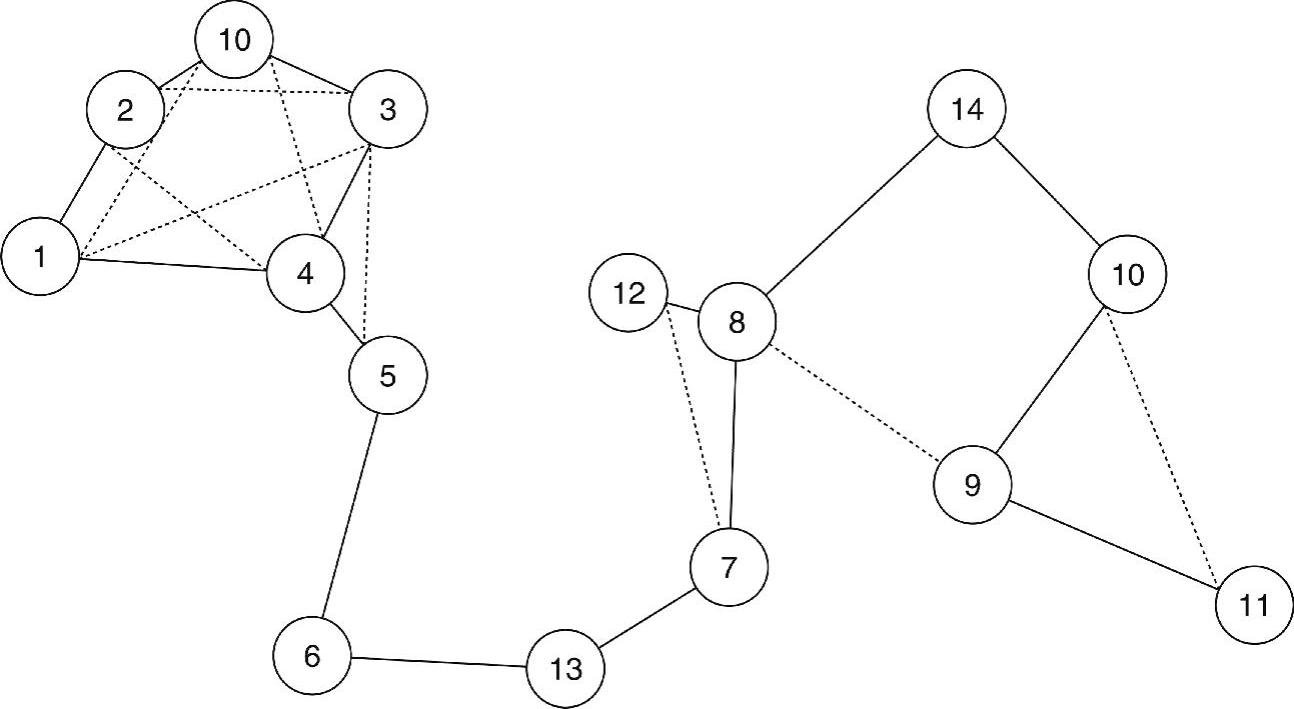
图2-19 单位圆盘图（所有边）中的LMST（粗线边）和RNG（所有非虚线边）

如果在任何三角形uvw（w是来自于节点集的任意第三个节点）中，如果uv不是最长的边，则边uv位于RNG中（参考文献（Toussaint，1980）对此进行了首次定义）。在图2-20中，如果在灰色区域（又称为禁区）不存在其他节点，则边uv属于RNG。对于任何位于禁区的点w来说，uv是三角形uvw中最长的边。使用上述标准，如果禁区内存在另一个邻居，一旦节点收集到所有邻居的位置信息（通过信标消息），则它能够针对每个边做出决策。因此，构建RNG不需要任何额外消息。RNG的平均度数为2.5（Hou et al.，2005）。RNG的平面性可以从其超集Gabriel图的平面性（第4章将对其进行描述和证明）中得出。

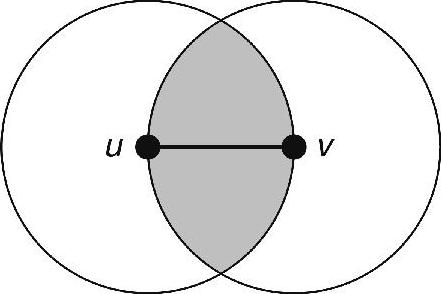
图2-20 RNG中边uv的禁区

在LMST（Li et al.，2003）中，假定每个节点u收集其单跳邻居的位置信息。然后，节点u计算其单跳邻居子图N（u）的最小生成树（MST）。当且仅当uv既位于MST（N（u））中，又位于MST（N（v））中时，边uv属于LMST。为了做出此决策，邻居之间需要进行消息交换（除了学习邻居的信标消息之外）。LMST的平均度数为2.04（Hou et al.，2005）。参考文献（Li et al.，2004）表明，LMST是一种平面图（它也是从超集RNG的平面性中得出的）。它们将LMST扩展至k跳邻居。也就是说，每个节点知道其k跳邻居的位置，且LMST是基于每个节点的k跳子图构建起来的。

定理2-3 （Ovalle-Martinez et al.，2004；Cartigny et al.，2005）：MST⊆LMST⊆RNG。(https://www.xing528.com)

证明：我们首先给出MST⊆LMST（Ovalle-Martinez et al.，2004）的证明，然后证明LMST⊆RNG（Cartigny et al.，2005）。这两个定理都是采用反证法来证明的。

假定存在属于MST但不属于LMST的边。假设e为这些边中最短的一条。假定在每个节点u的子图N（u）中，采用Kruskal算法（Kruskal，1956）来构建MST。也就是说，可以按照各边长度的升序，来逐一对各边进行考虑。在考虑边e时，由于它不包含在LMST中，因而它在LMST生成一个圆C，且e是圆C中最长的边（如图2-21所示）。一些来自于C的边不在MST中（否则由于e属于MST，因而存在着一个圆）。下面考虑由圆C构建的扩展圆C′。假定f是来自于C的一条边，且它不在MST中。将f添加到MST中，生成一个圆B，且f是圆中最长的边。圆B是由边f和一条包含来自于MST的若干条边的路径构成的。将圆C的边f用来自于该路径的所有边来代替。每进行一次替换，都会扩大圆C的范围，但不会添加比边f长的任何边，因而也不会添加比边e长的任何边。这种替换过程会在每一步中持续扩大圆C′的范围。最终，通过使用MST边对应的路径来替换所有非MST边后，边e仍然是圆C′中最长的边。但是，圆C′中的所有其他边目前也属于MST。这与MST不包含圆相矛盾。因此，MST⊆LMST。

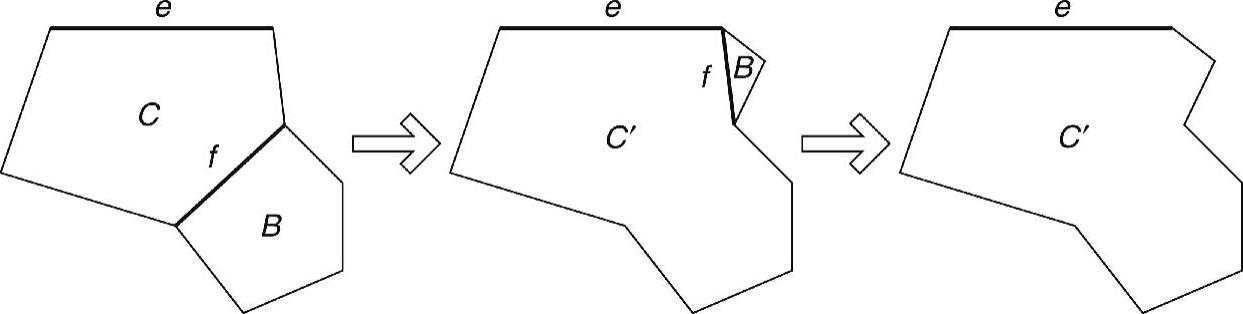
图2-21 反证MST⊆LMST：来自于MST的边e成为圆中最长的边

假定存在着一条边uv，使得uv∈LMST，且uv∉RNG。由于uv∉RNG，必定存在一个节点w∈N（u）∩N（v），且uv是三角形uvw中最长的边。由于uv∈LMST，无论是uw，还是vw，都不在LMST中（否则，LMST存在一个圆，而不是一棵树）。为了不失一般性，我们假定uw不在LMST中。边uv可以被MST（N（u））中的边uw所代替，从而导致MST中的总权重比原始MST树低，这是一对矛盾。因此，LMST⊆RNG。

需要注意的是，RNG中（LMST中也是如此）每个节点u的度数是有界的（通常取值5，特殊情况下为6），但仅当每条边的长度是不同时上述结论才成立（否则存在着RNG中某条边度数非常大的实例）。这很容易通过考虑使用记录

（uv，min（key（u），key（v）），max（key（u），key（v）））

作为上述定义中的新“长度”来实现。