高效洪泛与基于切片的广播技术

对于任何仅基于单跳邻居信息的洪泛方案来说，参考文献（Liu et al.，2007）提出了一种保证传送的充要条件。基于这种充要条件，提出一种称为高效洪泛的、基于发送方的洪泛方案。节点s的邻居区域是节点s所有邻居加上节点s本身的覆盖盘的并集。假设F（s）代表由节点s计算的转发节点集。

定理2-2 对于每个节点s来说，当且仅当节点s的邻居区域被F（s）被覆盖，参考文献（Liu et al.，2007）中的单跳洪泛方案能够实现保证传送。

针对每个转发节点s，基于定理2-2，可采用高效洪泛方案来计算最小F（s）。为了实现F（s）最小化，F（s）中的每个节点必须对节点s的邻居边界有所贡献。否则，在不影响F（s）覆盖区域的情况下，可以将该节点从F（s）中去除。

参考文献（Liu et al.，2007）提出了用于计算最小F（s）的两种算法。第一种算法的时间复杂度为O（n²），其工作原理如下：根据节点s的所有单跳邻居到节点s的欧几里得距离，将其按降序排列成一个表格。由于它必定对节点s的邻居区域边界有所贡献，因而列表中的第一个节点距离节点s最远，将包含在F（s）中。每次，列表中的下一个节点被添加到F（s），如果其覆盖盘没有完全被已构建的F（s）所覆盖。该过程将持续进行，直到考虑了列表中的所有节点。

第二种算法（Liu et al.，2007）用于计算节点s的邻居边界，这样对该边界有所贡献的节点都是F（s）中的节点。该算法的时间复杂度为O（n log n）。基本思路是采用成对边界合并方法，来计算节点s邻居区域的边界。首先，每个节点与另一个节点随机配对，并合并其覆盖边界。然后，合并的节点对边界再与另一个节点对边界进行合并。不断重复这种合并操作，直至仅存在一个大型合并边界，这是节点s邻居区域的边界。最小F（s）是由所有对该边界有所贡献的节点构成的。

源节点s首先计算其F（s），然后广播一条洪泛消息，该消息在F（s）中添加了节点ID。接收到洪泛消息之后，如果每个节点u的ID包含在消息中，且这是它初次接收到消息，则它完成与发送方相同的操作。否则，节点u忽略该消息。如果传输是理想的，即不存在碰撞和丢包，则根据定理2-2，网络中的所有节点最终将接收到洪泛消息。参考文献（Liu et al.，2007）进一步研究了转发节点优化问题。如果F（s）中某个节点所有的邻居已经被节点s或F（s）中的其他节目覆盖，则该节点不需要重传洪泛消息。如果优化过程中存在一个循环，则节点ID用于打破平局。(www.xing528.com)

参考文献（Khabbazian and Bhargava，2008b）提出了一种基于切片的广播算法，这是一种基于发送方的方案。与参考文献（Liu et al.，2007）提出的方案类似，它假定每个节点知道其单跳邻居的位置信息。每次，存储洪泛消息的节点推荐其单跳邻居子集（即转发集），来转发消息。接收到洪泛消息后，只有那些ID包含在消息中，且从来没有重传过消息的节点将转发消息。

为了选择转发消息的邻居，节点将其通信区（其模型为圆形）划分为凸出切片。在如图2-15a所示的实例中，存在3个具有相同半径的圆，每个圆的中心恰好位于其他两个圆的交点处。具有加粗边界的切片定义为节点A附近的凸出切片。确定了节点A的转发集，这样任一非空节点A附近的凸出切片至少包含来自于转发集中的一个节点。假定节点A开始计算其转发集。节点A从其邻居中，随机选择第一个节点S₁。假定当前所选的节点为S_i。如果S_i的凸出切片是非空的，则下一个节点S_i+1是节点S_i凸出切片最远的逆时针旋转。在如图2-15b所示的实例中，S_i+1是位于S_i凸出切片内的一个节点。如果S_i凸出切片内没有节点，则S_i+1是节点S_i凸出切片最近的逆时针旋转，参见图2-15c所示的实例。如果S_i要么位于S₁凸出切片内，要么S₁位于S_m凸出切片内，则S_m处的转发集的选择是完备的。作者证明，基于切片的广播算法能够在无碰撞网络中实现100%传送（Khabbazian and Bhargava，2008b）。

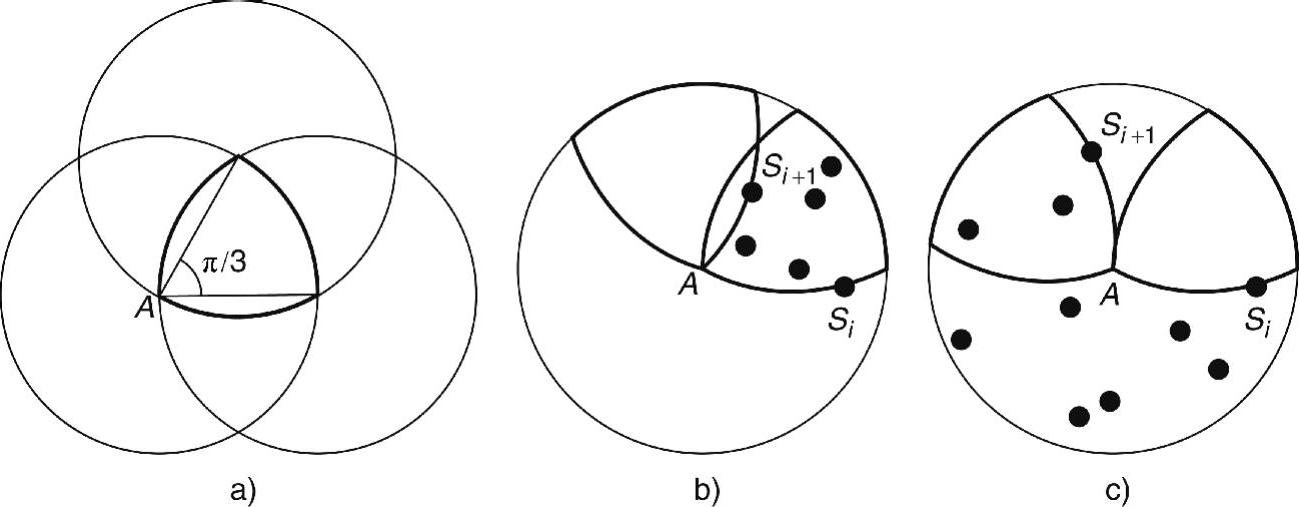
图2-15 基于切片的广播算法