基于覆盖的CDS分析方法

参考文献（Wu and Li，1999）提出了一种在一般图中构建CDS的局部算法。它假定每个节点知道其两跳邻居的局部拓扑。也就是说，每个节点拥有一个直接邻居列表和一系列邻居的直接邻居列表（可通过交换两轮“问候”消息来实现）。另一种方案是，每个节点知道自己的位置和所有邻居的位置（这需要通过交换一轮“问候”消息来实现）。在这种情况下，每个节点可以将自己的位置告知邻居节点。我们描述一个由参考文献（Stojmenovic et al.，2002）提出的改进定义（参考文献（Stojmenovic，2004）随后对该定义进行了修正和评价），它完全不需要发送任何附加消息（除了用于收集所需局部知识的上述“问候”消息）。更准确地说，每个节点可以自主决定它是否位于CDS中，而不需要与邻居交换任何消息。但是，为了获取邻居节点的CDS状态，可能需要进行通信。对于任意输入图，两种定义和构建算法（参考文献（Wu and Li，1999）和参考文献（Stojmenovic et al.，2002））通常会生成相同的CDS。同时，我们还假设每个节点具有唯一键值，且这些键值作为所需局部知识的一部分发送给邻居。

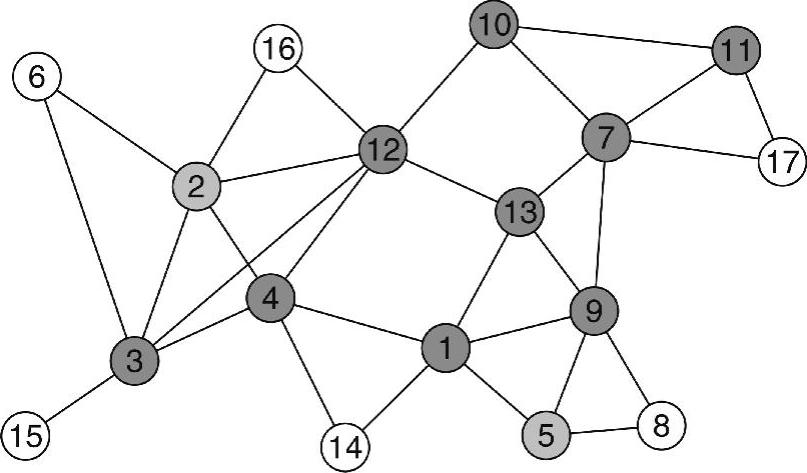
图2-6 基于覆盖的CDS算法

如果某个节点具有两个非连通邻居，则称该节点是0网关节点。如果一个节点（节点A）的每个邻居也是节点B的邻居，且A的键值小于B，则称节点A被邻居（节点B）所“覆盖”。如果节点A的每个邻居至少也是节点B或C的邻居，且A的键值既小于B，又小于C，此时称节点A被两个连通的邻居节点B和C所“覆盖”。一个未被任何邻居所覆盖的0网关节点将变成1网关节点。一个未被任何两个连通邻居所覆盖的1网关节点将变成2网关节点。最后，2网关节点形成一个CDS。需要注意的是，0网关节点和1网关节点也可以形成CDS，因为2网关节点是它们的子集。在图2-6所示的实例中，节点6、8、14、15、16、17不是0网关节点。节点5被其邻居节点9所覆盖，因为所有节点5的邻居也都是节点9的邻居，且5＜9（假定键值是按数字次序排列，1＜2＜…）。这样，0网关节点5不是1网关节点。节点2被两个连通邻居3和12所覆盖，因为它们具有较高的键值，同时剩余邻居4、6和16被两个连通邻居3和12所覆盖。因此，1网关节点2不是2网关节点。最后，剩余的2网关节点{1，3，4，7，9，10，11，12，13}形成一个CDS。

节点的键值既可以是其标识符（参考文献（Wu and Li，1999）），又可以是一个数对（度数degree，标识符ID）（Stojmenovic et al.，2002）（度数是一个节点的邻居数），还可以是一个三元组（能量energy，度数degree，标识符ID）（Wu et al.，2002，2003）。例如，当采用（能量，度数，标识符）时，具有较高能级的节点成为支配者的概率要高一些。如果两个节点的能级相同，则使用节点度数来打破平局。同样，如果两个节点的能级和节点度数都相同，则使用节点标识符来打破平局。对于某个键值来说，这种选择能够均衡节点能量，因为通常选择具有较高能量的节点处于激活状态。可以周期性地对决策进行重新评估，这样就可以延长网络的生命周期。基于节点度数和剩余能量水平，参考文献（Shaikh et al.，2003）提出了几种可选键值定义。奇怪的是，该文献推崇的定义是key（键值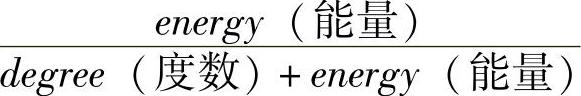）=，但对于该结果文献没有给出任何解释。

通过采用广义规则（Dai and Wu，2003），还可以进一步减小图2-6中CDS的尺寸。在这种情况下，覆盖可由任意数量的连通单跳邻居提供。在如图2-6所示的实例中，节点7被4个连通邻居9、10、11、13所覆盖，因为剩余邻居17被节点11所覆盖，且节点7的键值最小。这样，就可以从CDS中去除节点7。形式上，规则可以定义如下：假定N（u）代表节点u的连通邻居集，这些邻居的键值大于A。如果任一u的邻居要么在N（u）中，要么是属于N（u）的节点的邻居，则可以从CDS中去除节点u。这一规则表述是由参考文献（Stojmenovic et al.，2004）提出的，主要是为了避免邻居之间交换相似信息。根据这一定义，仍然属于CDS的节点称为网关节点。

用于验证这一条件的简单算法是由参考文献（Carle and Simplot-Ryl，2004）提出的。首先，每个节点检查它是否为0网关节点。然后，每个0网关节点u构建（原始UDG的）一个子图G_h，它是由具有较高键值的节点u单跳邻居和邻居之间的现有各边构成。如果G_h是空集或处于非连通状态，则u将加入到DS中去。如果G_h处于连通状态，但存在着u的一个邻居，它不是G_h中任意节点的邻居，则u也决定加入到DS中去。否则，u被覆盖，且不在DS中。Dijkstra最短路径算法可局部用于每个节点，来测试连通性。需要注意的是，邻居所需的连通性并不表示任意两个邻居都是单跳邻居，只是意味着这些节点的子图是一种连通图。

根据广义规则，我们将选择到DS中的节点称为网关节点（将上述定义进行推广）。存在着不被任何其连通邻居子集覆盖的节点。这样，每个未被选作网关节点加入到CDS中的节点要么是0网关节点，要么存在一个包含k个连通邻居的集合，节点被这些邻居所覆盖，它们具有较高键值。无法直接判断所谓的网关节点能否生成一个（连通的）DS。对于任意k来说，每个网关节点也是一个k网关节点。我们将给出CDS性质的证明。连通性的证明方法与参考文献（Wu and Li，1999）给出的方法类似，而DS性质的证明方法可以从参考文献（Stojmenovic，2004）给出的方法推广得出。

定理2-1 网关节点可以生成CDS。

证明：相反，我们假定网关节点生成的集合还是一个DS，则存在一些既不属于集合S，又不是S中任意节点邻居的节点。在这些节点中，假定节点X具有最大键值。如果X的所有邻居不是0网关节点，则此图是一个完全图。否则，假定Y是X具有最大键值的0网关邻居。由于Y不是网关节点，则它被其k个连通邻居U₁，U₂，…，U_k所覆盖（这不必是一连串的邻居），且Y在这些节点中具有最低的键值。可以先去除这些不是0网关节点的邻居，而不会影响到覆盖特性。在这些（剩余）0网关节点中，X必定是至少一个节点（如U_i）的邻居。但是，由于Y的键值小于U_i的键值，与Y的选择条件相矛盾。因此，既不属于集合S，又不是S中任意节点邻居的节点集合是一个空集，因此S是一个支配集。(www.xing528.com)

生成DS的连通性可以从去除任何节点的观测条件中推出，这些观测条件决定不参与CDS，生成DS的连通性不会断开节点S和节点D之间的任意现有路径。在图2-7所示的实例中，假定节点S通过路径S→…→A→U→B→…→D与节点D相连，该路径是由实边构成的。假定节点U不在DS中。也就是说，节点U被其连通邻居U₁，U₂，…，U_k中的k≥1个邻居所覆盖。在图2-7中，k=3。这样，节点A和B通过U₁，U₂，…，U_k连接起来。路径分段A→U→B可以被A→U_i→B代替。在图2-7中，A→U→B可以被A→U₁→U₂→U₃→B代替。因此，即使将U去除，仍然可以保持连通性。所有节点可以按照其键值进行排列，并行去除可看做是按照键值递增的次序，依次去除一系列节点。在每一步中，连通性都得到保持，因为先前去除的节点不会应用于新节点的去除中（每个节点仅被高键值邻居所覆盖）。

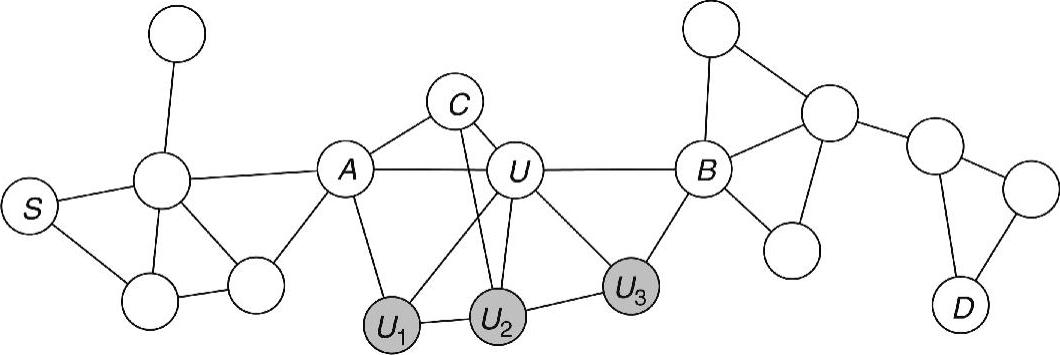
图2-7 网关节点的连通性

参考文献（Dai and Wu，2003）和参考文献（Ingelrest et al.，2007）进一步研究了增强型DS。这里我们给出用于计算DS的一种增强型定义。如果在中间节点u的两跳邻域内，存在着一个具有较高键值节点的连通集A_u，使得u的每个邻居要么属于A_u，要么是A_u中某个节点的邻居，则称中间节点u不是一个支配者。在图2-8a所示的实例中，应用了算法（参考文献（Wu and Li，1999））之后，所有黑色节点形成一个CDS。但是，其尺寸可以缩小，如图2-8b所示。由于节点a被两跳邻居{b，e，f}所覆盖，因而可以将节点a从CDS中去除。同样，由于节点b以及其所有邻居{a，c，e}被其连通高标识符两跳邻居{e，f}所覆盖，因而节点b也可以从CDS中去除。

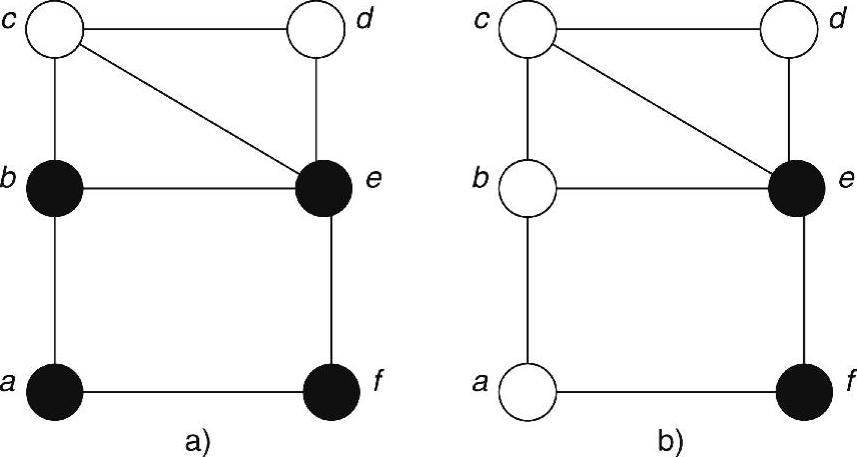
图2-8 CDS实例

a）采用广义规则的CDS b）增强型CDS

事实证明，参考文献（Wu and Li，1999）所提算法的性能比为O（n），其中n为网络中的节点数（Wan et al.，2004）。最坏情况下行为实例是那些位于正方形网格点（x，y）处的节点，其中（x，y）也可用作键值（具有较大传输数量，但又不是太大，例如n^0.5/2）。该网格的所有内点仍然位于CDS内。最坏情况下行为的一种更简单实例是键值递增的一系列节点（以及每个节点约n/2个邻居的传输半径），它迫使几乎所有的节点位于CDS中。但是，参考文献（Dai and Wu，2004）证实，广义CDS概念中包含一个固定平均近似比。参考文献（Wiese and Kranakis，即将发表）证实，在最坏情况下，基于单跳位置信息，不存在可以实现固定近似比的算法。证据主要是基于在两个同心圆上配置任意个节点的实例，节点之间的距离等于传输半径R，这样节点是成对的，每个圆内包含一个节点，成对节点之间的距离为R。如果uv是这种成对节点，基于邻居位置的局部知识，u和v都可以决定加入CDS，因为其他节点看起来与局部单跳子图的剩余部分之间是断开的。但是，在每个圆上，存在着一个包含固定数量节点的CDS，从而表明最坏情况下的近似比是无界的。

该算法的主要优势是通信开销（发送“问候”消息来获知邻居消息之后）和位置维护开销为零。假定节点移动或进行开/关转换，该算法仅需要节点的邻居们更新其状态即可。参考文献（Basagni et al.，2006）通过大量仿真实验，对该算法（Wu and Li，1999）（更确切地说，参考文献（Stojmenovic et al.，2002）所用到的上述算法变形）的性能进行了研究。结果表明，这是一种运行效率较高的算法，且与所有其他可选算法（本节已经对大多数算法进行了描述）相比，该算法能够在低消息复杂性和CDS尺寸之间实现最佳折衷。