基于集合覆盖的集中式算法优化方案

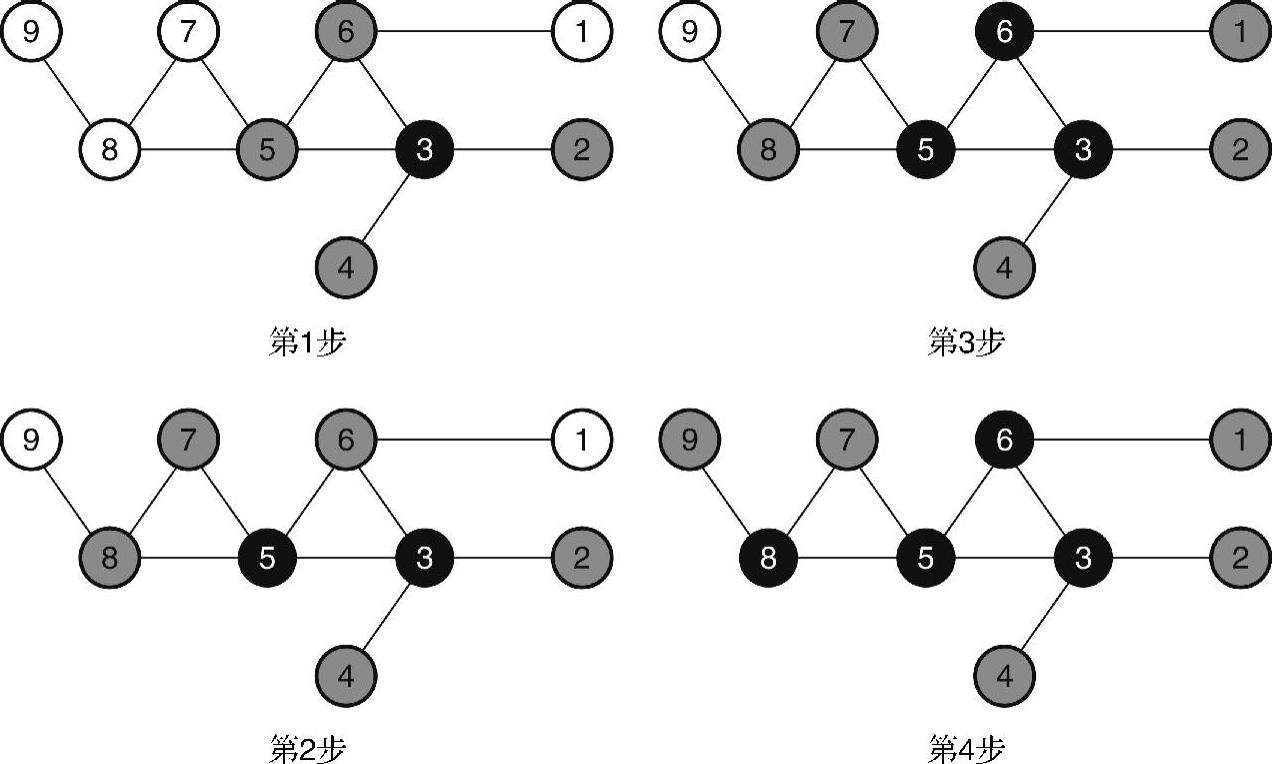
参考文献（Guha and Khuller，1998）提出了多种用于为一般图构建CDS的集中式算法。第一种算法的基本思路是通过单个节点向外来构建CDS。另一方面，第二种算法通过多个节点来同时构建CDS。第一种算法的工作过程如下：每个节点最初被涂成白色。接着，具有最大度数的节点被涂成黑色，而其所有邻居则被涂成灰色。然后，不停重复最后一步，直到图中不存在白色节点为止。每次具有最多白色邻居的灰色节点被涂成黑色，而其所有白色邻居则被涂成灰色。可采用节点标识符来处理多个节点度数相同的情况。最后，所有黑色节点形成一个CDS。算法原理如图2-4所示。节点3和节点5具有最大度数。由于3＜5，因而在第1步中，节点3被涂成黑色。节点3的所有邻居被涂成灰色。由于节点5具有最多的白色邻居，在第2步中，该节点被涂成黑色，而节点5的所有邻居被涂成灰色。同样，在第3步中，节点6被涂成黑色，而节点1被涂成灰色。当节点8被涂成黑色后，所有黑色节点{3，5，6，8}形成一个CDS。

参考文献（Cheng et al.，2003）证实，在UDG中存在着一种针对MCDS的多项式时间近似方案（Polynomial Time Approximation Scheme，PTAS）。这意味着对于任意给定的ε＞0，多项式时间近似的性能比可能是1+ε。但是，当ε趋近于0时，运行时间变得更快。这样，实际上PTAS是不适用的。参考文献（Min et al.，2006）提出采用具有最少Steiner节点的Steiner树（ST-MSN）来构建一个MIS。

(www.xing528.com)

图2-4 用于构建CDS的Guha-Khuller算法

参考文献（Min et al.，2006）提出的算法包括两个阶段。在第一阶段中，构建一个MIS（Wan et al.，2004），这样MIS的每个子集与其补集之间的距离为两跳。假设I代表MIS，A代表I的任一子集。A和I—A之间的距离恰好为两跳。也就是说，一定存在a∈I，b∈I—A，使得a与b之间的距离为两跳。需要注意的是，MIS也是一种支配集（DS）。MIS中的所有节点被涂成黑色，而所有其他节点被涂成灰色。在第二阶段，与至少三个连通黑色节点相邻的灰色节点被涂成黑色。如果没有节点满足这个条件，可以将与至少两个连通黑色节点相邻的灰色节点涂成黑色。最后，所有黑色节点形成一个CDS。对于UDG来说，算法的近似比约为6.8。这意味着CDS中节点数最多是单位圆盘图（UDG）MCDS中节点数的6.8倍。