SSPM射线光学分析

上述QPF的一个可行的物理实现方案是利用一个离焦的高斯光束在样本平面上引入一个二次相位的波前分布，如图9－3所示。

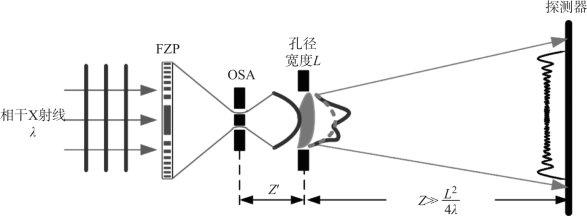
图9－3　利用散光照明的SSPM实现方案

注：样本置于离焦位置，抛物面相位波前被引入样本上；在远场测量衍射图样。

入射的X射线光束由一个菲涅尔透镜（Fresnel Zone Plate，FZP）聚焦，并将一个阶数分选孔径（Order Sorting Aperture，OSA）置于焦点上，使得仅1阶衍射光能够通过。这种设置方式最初由Nugent等提出，通过产生曲面波前照明来解决相位提取的二义性问题［279，309］。他们的工作近年来已经发展成为一种新的X射线衍射成像方法，菲涅尔相干衍射成像（Fresnel Coherent Diffractive Imaging，FCDI）［278，310－312］，尽管该方法工作于Fraunhofer远场。

将样本置于离焦位置Z′，则照射到样本上的高斯光束的复振幅为［313］

式中，C（Z′）为一个样本平面上不依赖于坐标（x，y）的因子；R（Z′）为波前在位置Z′处的曲率半径［313］。

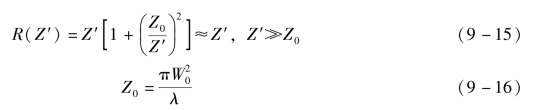
式中，W0为高斯光束的腰宽（焦点处光斑尺寸的一半）；Z0定义为瑞利距离（Raleigh range）。

本章研究a（x，y）对远场测量衍射图样的扩频调制效果，可以忽略振幅变化项C（Z′）·exp［－π（x2＋y2）／（2λZ′）］。该简化的合理性在于，F｛exp［－π（x2＋y2）／（2λZ′）］｝仅为一个实高斯函数，其扩频能力远弱于F｛exp［iπ（x2＋y2）／（2λZ′）］｝，后者的频谱几乎是平直的，如图9－2所示。因此，式（9－14）可简化为

基于孔径的这种二次相位形式可以限制式（9－17）中的相位分布，以满足扩频调制条件：

这导致(www.xing528.com)

利用高斯光束照射样本时，还存在一个隐含约束，即光束直径大于孔径尺寸。

而光束半径为［313］

式（9－15）和式（9－19）表明L≥2λZ′／d。近似地，式（9－16）、式（9－20）和式（9－21）表明L≤2W0Z′／Z0。由此可以导出SSPM的空间分辨率极限：

式（9－17）中的QPF的截止频率由下式给出：

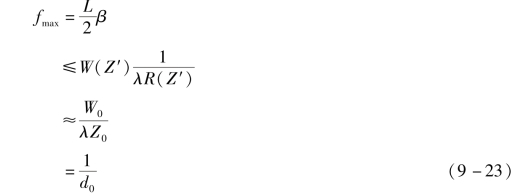
将式（9－19）和式（9－22）代入式（9－23）导出的β≤2／Ld0，有

从而给出了Z′和W（Z′）最小取值：

在任何离焦位置Z′＞Z′min，参数β将变小。因此孔径带宽BWa将随着Z′的增加而线性降低。如果希望样本分辨率小于d0，即d＝d0／M，M＞1，则孔径带宽BWa将为样本带宽的分数，即BWa＝BWψ／M。

可能存在质疑，现有FZP的分辨率将限制SSPM效能的完全实现：目前FZP的光斑尺寸（2W0）约为20 nm，则d0将超过——远大于CXDI所希望达到的成像分辨率。但是在实验部分的数值结果显示，即使QPF的带宽仅为样本带宽的1／8，相位调制器仍然表现出有效性能。此外，当照射光束与样本间存在相对运动时，横向（x和y）或纵向（z），样本上将被引入不同的二次相位波前。该特点有利于方便地实现不同的相位调制，因此当利用多次测量来提高重建质量时具有重要意义。