优化二次相位滤波器的相位滤波效果

一个复高斯函数的傅里叶变换仍然是一个复高斯函数［307］：

其具有瞬时角频率d（βt2）／dt＝2βt，β，t∈R。在信号处理中，是个二次相位滤波器（Quadratic Phase Filter，QPF）。

式（9－7）中QPF的傅里叶变换的模一致为1，本章据此导出所需孔径的相位分布。具体来说，相位为一个有限鸣叫声函数。

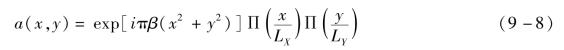
式中，LX×LY为孔径尺寸；矩形函数Π（t）＝1。若则其他为0。注意到a（x，y）是可分离的，其傅里叶变换可表示为

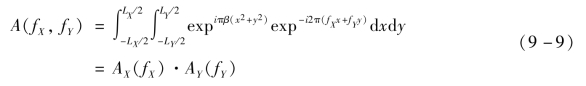
其中的一维谱为［308］

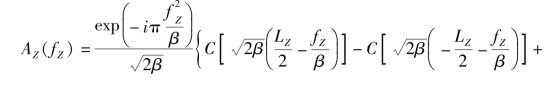
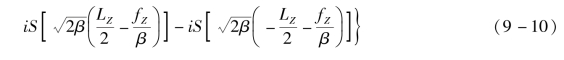(www.xing528.com)

式中

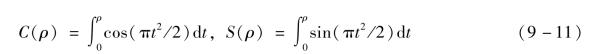
当相位函数φ（x，y）可以很好地被其一阶泰勒展开所逼近时，φ（x，y）的傅里叶变换频率与其局部频率将呈现高度一致性，即

这揭示了二次相位函数的一个有趣特性：孔径a（x，y）的谱也基本局限在一个大小为βLX×βLY的矩形区域中。对于二次相位分布，（βLX／2，βLY／2）是可通过QPF的最高频率的好的估计。图9－2中显示了一个二维QPF的平直傅里叶谱，其截止频率与最高局部频率相一致。

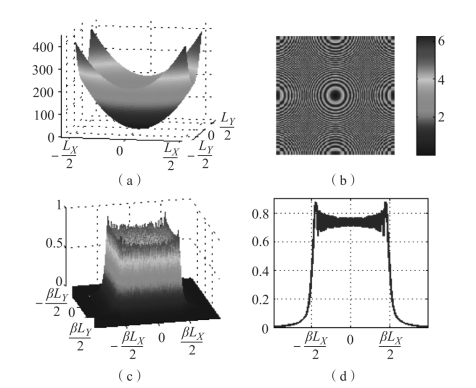
图9－2　二维QPF及其归一化MTF，L＝256，d＝2，β＝1.01×2／（dL）

（a）尺寸为L×L的孔径相位分布；（b）相位图mod［φ（x，y），2π］；（c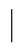）A（fX，fY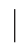），（a）的MTF；（d）横截面A（fX，0）

令孔径平面上物的分辨率为d（物的最小不可忽略横向尺寸），下面建立参数与孔径尺寸L（假设LX＝LY）和d之间的关系。物的单侧带宽为BWψ＝1／d。要求孔径的MTF完全覆盖物的频谱，即BWa≥BWψ，将得到如下的拓扑条件。