深入了解编码孔径CXDI基础知识

在成像原理上，CXDI与晶格成像方法相同：利用高度相干的X射线光束照射样本，并由光电探测器测量散射X射线强度，近场由Fresnel模型描述，远场由Fraunhofer模型描述。由于探测器仅能测量强度信息，而丢失了样本出射波场的相位信息，因此需要通过相位提取算法来获得相位分布进而恢复样本的复透过率。一旦计算出样本透过率，即可进一步估算其折射率和样本内介电系数分布，并最终根据电子密度推算样本的分子构成结构。

本章在经典CXDI实验布局中引入一个编码孔径（也可称为波导），设该孔径具有空间分布a（x′，y′），并被放置于样本前（图9－1（a））或后（图9－1（b））。如图9－1（a），紧邻样本后侧的纵向平面定义为物面，其上的出射场记为ψ（x，y）。

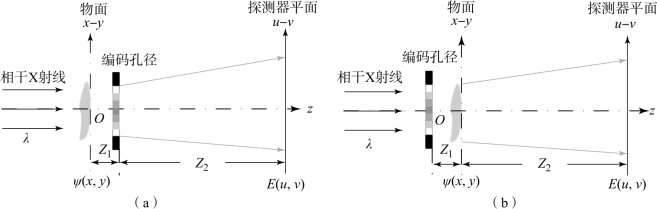
图9－1　编码孔径CXDI成像方案

（a）编码孔径位于样本后；（b）编码孔径位于样本前

两种方案中，感兴趣信号均是样本透过率函数ψ（x，y）与孔径函数a（x，y）之积，二者通过光场的自由传播算子相关联。

假设样本与孔径模板均为薄物体［306］，即其厚度满足Δz＜d·s／λ，d、s和λ分别代表物的分辨率、侧向尺寸和照射波长，则在z＝Z1处的出射场为

式中，a（x，y）＝P（a（x′，y′），Z1）为a（x′，y′）自由传递距离Z1后的分布，而P（·，·）为光场自由传递算子。由于光场的自由传递，故图9－1（a）和（b）中编码孔径对潜在信号ψ（x，y）的调制作用是相同的。(www.xing528.com)

在旁轴近似的条件下，探测器平面上的复振幅E（u，v）可由Fresnel衍射积分表达，即

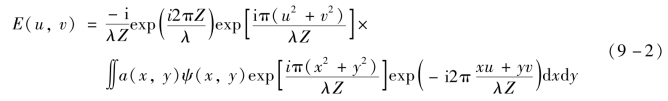
其正比于a（x，y）ψ（x，y）exp（iπ（x2＋y2）／λZ）的傅里叶变换。在Fraunhofer近似下，二次相位项可忽略，则E（fX，fY）∝F｛T（x，y）｝，fX＝u／λZ，fY＝v／λZ，而F｛·｝为二维傅里叶变换算子。探测器仅能获得强度测量：

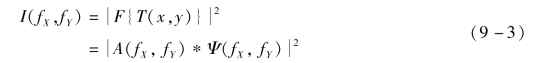
由于功率谱密度与自相关构成一个傅里叶变换对，式（9－3）可重写为

式中，RT（x，y）为T（x，y）的自相关函数，即

显然调制后信号T（x，y）应该具有很窄的自相关函数以降低衍射图样的动态范围。大部分已有调制方法利用随机调制，但是其效果极度依赖于调制单元间变化的尖锐性。本章将在后面部分证实这一点。