1.滤波器数量影响
这个实验用前面学习到的两个字典来进行CCT重建,并比较它们的结果。为了验证字典的泛化能力,使用了两个测试集:测试集1,包含图8-4中的4张图像(1)~(4),它们通过随机选择的方式从训练集合中提取;测试集2,包含图8-4中的4张图像(10)~(13),它们是随机地从光谱图像数据集ICVL[250]中得到。所有测试图像的维度为256×265×31。使用这些测试图像,可以按照式(8-26)中的成像模型仿真生成多个二维光谱层析测量,作为算法8-2的输入。

图8-4 测试图像集合
表8-1中给出了两个测试集上的平均重建PSNR值。首先,测试集2的重建结果并不显著低于测试集1的结果,甚至在4个观测采集情况下精度更高。这验证了CDL可以提取到具有泛化能力的图像卷积先验。第二,在所有测试中,50滤波器的结果总是稍低于25滤波器结果。这揭示出,一方面25个卷积核已经可以成功学习到高光谱图像中的本征特征,另一方面使用更多的卷积核意味着需要估计更多的未知卷积系数,从而影响最终重建结果。因此,在后面的实验中,将使用25卷积核字典。
表8-1 CCT重建的平均PSNR指标dB

2.重建算法的鲁棒性
这个实验用于验证重建算法的噪声鲁棒性。对上述测试集添加高斯噪声,其信噪比SNR等级从10 dB变化到40 dB。图8-5绘出了在各SNR等级下相对均方根误差(MSE)曲线。首先,因为单次曝光测量数据的采样率低到1/31,可以看出在各SNR等级下重建结果均是失败的。同时,在SNR=10 dB等级这个极端强噪声情况下,所提算法也无法从与信号具有同等噪声水平的观测中恢复原始信号。然而,从SNR=20 dB开始,误差曲线开始展现出MSE与SNR的理想关系:在4次观测—8次观测、8次观测—12次观测这两组曲线中,可以看出MSE降低数值之比基本为2∶1,这对应着它们各自的观测数量之比。也就是说,增加更多的观测数据能够带来重建误差的成比例下降。
 (https://www.xing528.com)
(https://www.xing528.com)
图8-5 不同观测数量下MSE-SNR曲线
3.高空间分辨率光谱图像重建结果
这个实验用图8-4中的16张测试图像来验证高空间分辨率光谱图像的重建性能,其空间维尺寸为512×512。由于图8-5的结果显示,12次观测、SNR=30 dB是一个比较合理的设置,故此实验用这种方式进行。为了比较CDL相对于传统解析稀疏基的优势,此处使用了CACCT[183]作为对比测试。可见本章算法在全部测试图像上都优于CACCT重建结果。重建峰值信噪比见表8-2。
表8-2 重建峰值信噪比dB
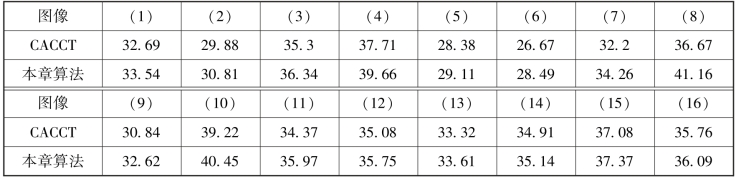
图8-6中显示了来自Harvard数据库的高光谱图像重建结果[182]。由于本章方法融合了CSC高光谱先验与PADMM优化策略,故其在高频成分的恢复上明显优于CACCT。
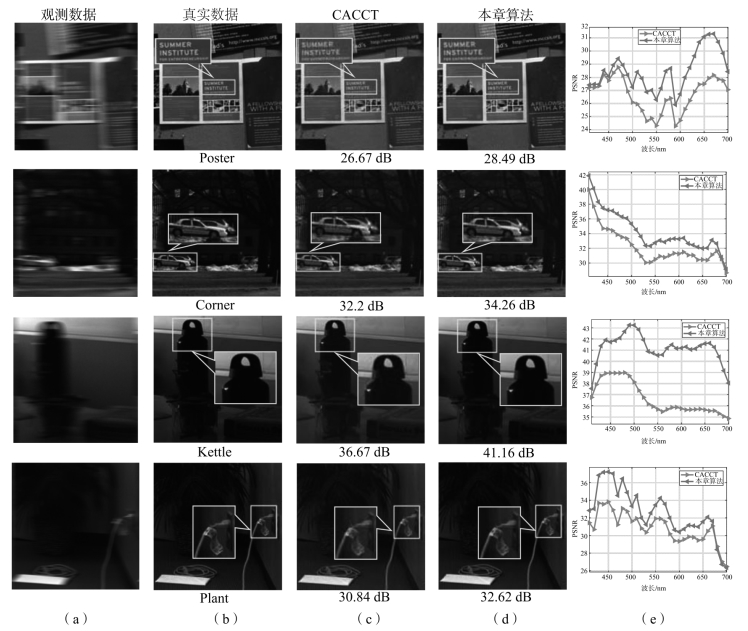
图8-6 重建高光谱图像的RGB显示
(a)观测图像示例;(b)真实光谱降维图像;(c)CACCT结果;(d)本章方法结果;(e)每个光谱通道的重建PSNR
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




