【摘要】:图8-1中给出了CTHIS的原理。设FPA上的坐标轴方向为w和h,则波长相关的平移量为图8-1层析光谱成像结构图注:直视棱镜在不通旋转角度下采集的二维观测数据g(w,h)的频谱对应着三维傅里叶变换中不同的二维切片。根据式进行空间平移的光谱图像在光谱维被FPA所积分[140,183],这在数学上遵循Radon变换,并且与平行X射线层析成像具有相同的数学模型,这也是光谱层析成像名字的由来。
层析光谱成像CTHIS于20世纪90年代首先被Mooney等[140]提出,其具有高光学通量的优势,这对于微弱目标的高光谱测量及成像光谱仪的小型化设计至关重要。图8-1中给出了CTHIS的原理。直视棱镜DVP放置在准直空间中,其旋转会引起各谱段光谱图像在焦平面阵列FPA上的平移。设FPA上的坐标轴方向为w和h,则波长相关的平移量为

图8-1 层析光谱成像结构图
注:直视棱镜(DVP)在不通旋转角度下采集的二维观测数据g(w,h)的频谱对应着三维傅里叶变换中不同的二维切片。
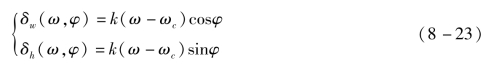
式中,k为DVP的色散系数;ω为波长;ωc和φ分别为DVP的无偏转中心波长和旋转角度。
根据式(8-23)进行空间平移的光谱图像在光谱维被FPA所积分[140,183],这在数学上遵循Radon变换,并且与平行X射线层析成像具有相同的数学模型,这也是光谱层析成像名字的由来。原始的CTHIS重建算法是在傅里叶域中求解一个过定的线性系统方程,但本章方法基于压缩感知原理[131,243]探索压缩光谱层析重建,从远小于光谱谱段数量的少量几个光谱层析投影测量中重建三维光谱数据立方体。(https://www.xing528.com)
将顺序排列的光谱数据立方体记为x∈RH×W×B,而DVP旋转角为φl下的测量向量,记作gl∈RH×W,则离散CCT模型可以写作:
![]()
式中,前向系统矩阵![]() 代表对所有B个平移的光谱谱段的求和,而Alb,b∈[B]实现对光谱谱段b的空间平移[183]:
代表对所有B个平移的光谱谱段的求和,而Alb,b∈[B]实现对光谱谱段b的空间平移[183]:
![]()
式中,F是为傅里叶变换矩阵,![]() 和
和![]() 是式(8-23)中定义的图像空间平移。
是式(8-23)中定义的图像空间平移。
最后,假设有L个由式(8-24)所定义的观测数据,将其级联得到如下线性系统。
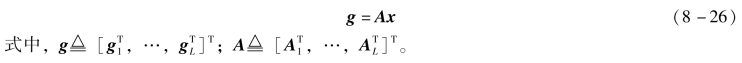
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




