卷积稀疏编码的子问题优化

当固定卷积核｛Dk，b｝时，使用第7章中从Dk，b构造卷积矩阵λk，b的方法，卷积稀疏编码子问题可写作

式（8－2）是非平滑凸函数，此处使用ADMM来求解。引入辅助变量sj＝Dzj和tj＝zj，式（8－2）的增广拉格朗日函数为

由于M是对角矩阵，求解sj是简单的。然而，由于尺寸为KN×KN，逆矩阵［DTD＋r（z）I］－1的计算成为真正的困难。这可以通过频率域内卷积矩阵的对角化来解决。

此处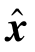，代表x的DFT。然而，与单通道CDL情况不同，式（8－5）中的三维卷积核结构使得无法直接应用矩阵逆引理来求解［206］，下面详细分析的矩阵结构，进而给出基于变量重排的解决方案。

1）式（8－5）的变量重排

式（8－5）中的矩阵具有以下稀疏结构。(www.xing528.com)

是由K×K个矩阵块构成，其中每个矩阵块为一个N×N的对角阵。通过变量重排，式（8－5）可以被分解为N个独立的小问题求解。

式中，为在空间频率位置n上采集所有K个卷积核的B个光谱通道上的DFT值；包含式（8－6）中每个矩阵块的第n个对角线元素；以同样方式提取。

2）式（8－7）的计算复杂度

式（8－7）有三项预处理计算开销：i）D的FFT，O（KBN logN）；ii）式（8－6）中的计算，O（BNK2）；iii）Hn＋r（z）I的逆矩阵计算，O（NK3）。式（8－7）自身的计算负荷在于两项矩阵—向量乘法，为O（JNK（K＋B））。如果将［Hn＋r（z）I］－1缓存起来，这部分预处理开销是平摊到ADMM算法的多次内循环上的，但是要以额外的内存消耗为代价。