PCDL的收敛条件：优化方法

当用式（7－12）替换式（7－10）进行卷积核更新计算时，一个自然的问题是：在何种条件下算法7－1收敛到以下鞍点问题的一个最优解：

式中，F和G为准下连续特展凸函数（proper，convex and lower semi－continuous functions）；dom F≜｛x∈X：F（x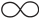）＜＋｝为函数F的定义域，类似地，dom G表示G的定义域；γ∈Υ为约束项Ad＋Bp＝c对应的拉格朗日乘子，而Υ表示对偶空间。

PADMM算法［212］结果表明，按照如下方式对变量d和p进行预条件化更新：

序列｛di，pi｝强收敛于式（7.16）的一个鞍点，如果满足如下条件：

（1）AHA＋∂F与BHB＋∂G是强单调的。

（2）N－AHA≥0，L－BHB≥0，预条件矩阵N与L为有界范数厄米特矩阵。

需要注意的是，式（7－8）中含有三个原始变量d、u和v。为了建立PCDL的收敛条件，本节将式（7－7）中的增广拉格朗日函数变换成式（7－16）中的两个变量块的标准形式。(www.xing528.com)

式中，G（p）≜E（u）＋R（v）。

式（7－17）与式（7－7）之间的等价关系可以通过以下过程证明。

首先，d的更新公式为

将对偶变量αd和βd分别替换为可见式（7－18）～式（7－20）与式（7－8）是相同的。

对于PCDL，条件（1）成立，因为：首先，保证了其强单调性（strongmonotonicity）；另一方面，由于G是特展凸函数，其准微分算子（subdiffer⁃ential operator）∂G是单调的［214］，而单位算子I的存在使得BHB＋∂G＝I＋∂G是强单调的［214］。条件（2）仅要求选择预条件矩阵时满足N≥AHA，因为此处并不要对变量p做预条件化处理，即取L＝BHB。