卷积运算中的边界处理与模板矩阵应用：相关工作探究

卷积运算涉及卷积边界的处理问题，其对CDL的结果会产生重要影响［197，202］。为去除边界问题的影响，首先可以将所有训练图像进行边界补零到尺寸L＝（H＋h－1）×（W＋w－1）［190，191］；同时，为充分利用FFT进行快速计算，卷积核也通过补零插值到相同的尺寸L。该补零过程可以通过一个插值矩阵P来实现［206］。然后在目标函数中引入一个模板矩阵，以将边界元素排除在外［197，207］。此外，该操作还有利于从部分图像像素中进行CDL［208］和图像修复应用。由此，考虑边界因素的目标函数为

为简便起见，本章此后的表述中将直接用Dk∈和分别表示由dk和zj，k构造的循环块—块循环卷积矩阵。值得注意的是，卷积运算dk∗zj，k的矩阵—向量形式既可以写作Dkzj，k，也可以写作Zj，kdk，这将视对哪个未知变量进行优化而定。

在式（7－5）中固定系数z，d—子问题等价于如下的无约束问题。

式中，系数矩阵Z≜［Z1；…；ZJ］，Zj≜［Zj，1，…，Zj，K］，j＝1，2，…，J；而卷积核构造为d≜［d1；…；dK］；图像写作b≜［b1；…；bJ］；目标矩阵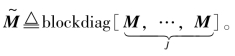示性函数ΓC（·）将卷积核限制在凸集C＝｛dk∈RL：（I－PPT）dk＝0，‖dk‖≤1｝之内，即卷积核的原始尺寸与单位范数球的交集［201，204］。

引入辅助变量u＝Zd和v＝d，式（7－6）的增广拉格朗日函数可写作：

式中，为惩罚因子，则各个ADMM变量按以下次序依次更新。(www.xing528.com)

相同的ADMM优化方法可用于求解CSC子问题，只需做函数替换R（v）≜‖v‖1。而且，CSC子问题有频域中的快速算法［201］，该部分内容将在7.3.2节介绍。相比较而言，滤波器更新子问题的计算复杂度更高，因此本章内容围绕该问题的优化求解展开。

可以看出，式（7－8）中的变量d、u和v子问题对应着迫近算子并有闭合解［209］，并且u和v可通过逐点计算，参见后面的算法7－1。但是d的求解涉及大型逆矩阵（ZTZ＋的计算。为获得可行的d变量求解方法，Bristow等［198，206］利用FFT将卷积矩阵｛Zj，k｝对角化（此处，a＾和A＾分别代表a和A的频率域表示），并且通过对JL×KL的稀疏矩阵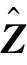的元素重排，可构成块对角矩阵，每一个矩阵块的尺寸为J×K。每一个矩阵块对应一个最小二乘问题，共有L个这样的K×K线性独立系统。因此，这种直接采用逆矩阵计算的算法具有复杂度O（LK3）。为对算法进行加速，Heide等［197］在每一次卷积核子问题中将逆矩阵缓存下来，但是要以更高的内存消耗为代价［201，202］。Wohlberg［201］提出了一个迭代Sherman－Morrison方案来求解各K×K线性子系统，具有计算复杂度O（J2LK）。由于这些方法均依赖于确切矩阵求逆，因此对图像数量J、滤波器个数K存在二次甚至三次依赖。本章提出一种对角预条件处理滤波器子问题式（7－8）的方法，以避免（ZTZ＋的显式计算，获得的计算复杂度为O（JLK）。在避免CDL中的稠密矩阵求逆问题上，文献［202］提出的BPG_M算法采用迫近梯度下降的优化策略。BPG_M使用PB和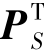分别代表卷积核补零矩阵和图像边界截断矩阵，对于其滤波器更新问题所涉及的系统矩阵Ψ＝PBZ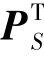，通过寻找对角优超矩阵MΨ≥（Ψ）TΨ来逼近式（7－6）的线性化迫近的上界。本章基于PADMM（Precondi⁃tioned ADMM）的字典学习算法相对于BPG_M的优势在于：

（1）在BPG_M中，Z、PB及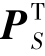耦合在一起，这使得难以通过对矩阵ΨTΨ的谱分析获得紧的优超矩阵MΨ，因为在其推导过程中会略掉PB，从而引起一个过度松弛。而本章方法利用ADMM灵活的变量分离特性，将PB、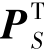与Z分离开来，直接从Z＾HZ＾推导出对角的预条件处理矩阵，从而避免了PB、的影响（参见7.3.1节）。

（2）PB和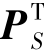均不能通过傅里叶变换对角化，BPG_M必须频繁地在空间域与频率域之间切换，这显著地增加了运算量。而本章算法在频率域中通过变量重排，将原始的大规模线性方程组分解为若干个小型方程组求解，从而可以快速地通过对每个小方程组系统矩阵的谱半径计算，来获得所需的预条件矩阵（参见式（7－21））。