压缩光谱层析成像的高光谱数据集实验结果

为验证压缩光谱层析成像的可行性，本节给出利用真实高光谱数据集进行仿真层析重建的结果。所用光谱图像数据来自哈佛大学的CZ高光谱数据库［182］，包括室外日光照明和室内人造光混合照明两类场景的光谱数据。所有原始数据的规模为1 392×1 040×31，覆盖光谱范围为420～720 nm。实验从室外和室内数据集中分别挑选了两组数据，并截取成384×384×30大小用于算法验证的真实数据（室内：Kettle／Plant；室外：Poster／Corner）。

所有层析成像过程和重建算法均由MATLAB编程实现（未经C和MEX优化），其软硬件资源为：AUSU X81笔记本电脑，Windows XP操作系统，MATLAB2012b（32 bit）；2.0 GHz Intel Core2 Duo CPU T5750，2 GB内存。

4组实验中，在12个位置上将直视棱镜DVP的旋转角度设置为2πl／12，l＝1，2，…，12，这相当于30%的数据采样率。在图5－10、图5－12、图5－14和图5－16中绘出了重建相对误差曲线：各图中上部为各通道光谱图像的重建相对误差，其中有个别谱段的重建相对误差显著增大，且不同数据集中大误差谱段并不固定，这可能是由于这些谱段图像的主要空间频率成分远离层析采样点位置所致；下部为逐次迭代误差，可见算法在20次迭代后重建误差已基本稳定。算法运行时间约为63 s。

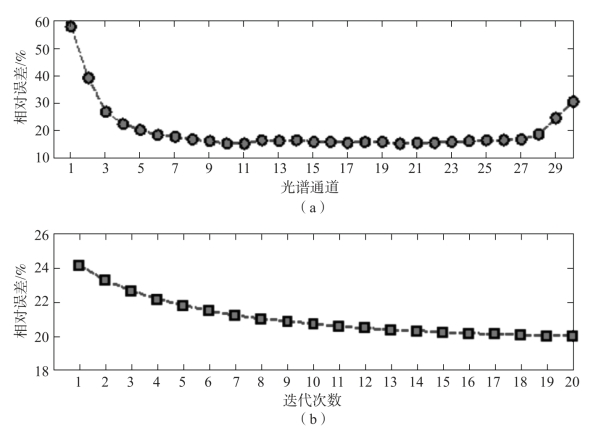
图5－10　Corner重建相对误差

（a）各通道光谱图像的重建相对误差；（b）光谱数据立方体重建的逐次迭代误差

在图5－11、图5－13、图5－15和图5－17中绘出了4组数据的最优与最差重建谱段图像，以及对应谱段的原始图像和基于频域采样数据IFFT的反向投影算法重建结果，以供视觉比较。可见本章的TV规整化重建算法对抑制图像中的“振铃”效应具有显著作用，同时边缘成分也得到很好的保持。

图5－11　Corner最优与最差重建谱段结果

（a）最优重建谱段；（b）最差重建谱段

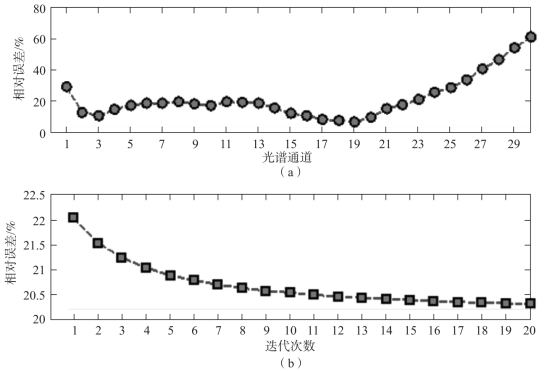
图5－12　Kettle重建相对误差

（a）各通道光谱图像的重建相对误差；（b）光谱数据立方体重建的逐次迭代误差

(www.xing528.com)

图5－13　Kettle最优与最差重建谱段结果

（a）最优重建谱段；（b）最差重建谱段

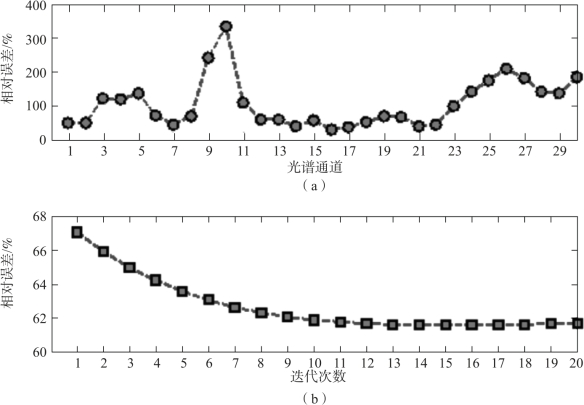
图5－14　Poster重建相对误差

（a）各通道光谱图像的重建相对误差；（b）光谱数据立方体重建的逐次迭代误差

图5－15　Poster最优与最差重建谱段结果

（a）最优重建谱段；（b）最差重建谱段

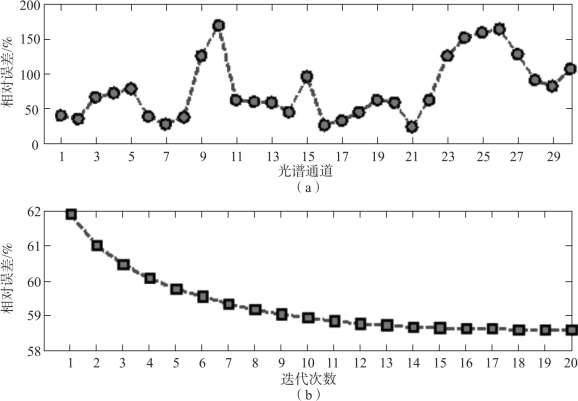
图5－16　Plant重建相对误差

（a）各通道光谱图像的重建相对误差；（b）光谱数据立方体重建的逐次迭代误差

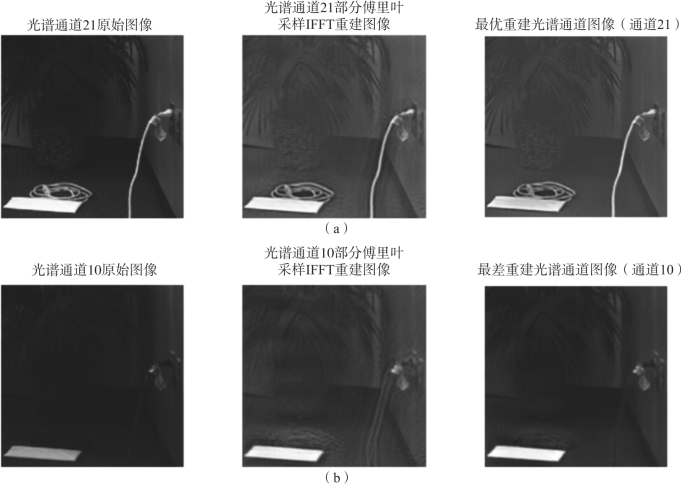
图5－17　Plant最优与最差重建谱段结果

（a）最优重建谱段；（b）最差重建谱段