傅里叶域快速重建算法

高光谱图像的稀疏性体现在数据中存在着高度的空间相关性和光谱相干性，因此无论是式（5－1）中的l1最小化还是式（5－2）中的TV最小化优化策略，都能用于求解式（5－9）。但是对于图像复原来说，只要图像梯度是稀疏的，TV规整化［179］比l1规整化能够更好地保留图像边缘［131］。因此，本章将选择三维TV作为光谱数据立方体f的空间—光谱联合稀疏性约束。

式中，‖·‖为向量的2范数；为一阶微分算子；Dif的三个分量分别是体素i位置上的x、y和λ方向上的一阶有限微分。

至此，原始光谱数据立方体通过如下拉格朗日问题求解。

式中，α＞0控制着规整化与重建精度之间的平衡。但是由于TV算子本身既非线性又不可微，故难以直接求解式（5－11）。我们采用如下的变量分离方法［180，181］，将Dif从不可微项‖·‖中分离出来。

引入辅助变量W＝［w1，…，wN］，wi∈R3，则式（5－11）等价于：

式中，惩罚因子β＞0控制着wi和Dif之间的偏离程度。显然式（5－12）中的代价函数关于（f，W）是凸的，并且固定其中一项时，另一项有闭合解。因此按如下方式交替优化W和f。f－step：固定f，则式（5－12）等价于求解(www.xing528.com)

其唯一解由如下的二维shrikage公式给出［181］。

W－step：固定W，则式（5－12）等价于求解二次型。

式中，D（j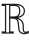）∈N×N，j＝1，2，3，分别为x、y和λ方向上的有限一阶微分矩阵，它们各自的第i行共同构成梯度矩阵Di；ω（j）＝［w1（j），…，wN（j）］T。

由于在周期边界条件下微分矩阵D（j）可被三维DFT矩阵F对角化，＝FD（j）FT和PTP同为对角阵。因此，可以在傅里叶内逐点求解

当ω（j）固定时，式（5－17）的主要运算负荷为3次FFT和1次IFFT（Inverse FFT）。