压缩光谱层析成像模型优化

首先回顾一下光谱层析模型CTHIS，如图5－6所示，一个CTHIS由物镜、旋转的直视棱镜DVP和相机组成［140］。随着DVP绕光轴旋转，一个空间物点的中心波长（由DVP决定）在FPA上的成像位置保持不变，而其他波长像点将绕中心波长点环绕，环绕半径由波长和DVP的色散常数决定。相机在DVP每个旋转角度下记录的复用图像，都对应着三维频率立方体中过原点的一个切片。Brodzik和Mooney给出了基于凸集投影和PCA的频域迭代重建算法［147］，解决了病态系统方程矩阵条件下的光谱图像过定重建问题——通常所需的观测次数为光谱谱段数的1.3倍。因此，高的光谱立方体采集率对相机帧频提出了很高要求，如一个256×256×64的光谱数据需要955 Hz帧频才能获得10 Hz的立方体采集率［178］。

图5－6　CTHIS组成及工作原理

注：DVP的旋转使得空间场景在FPA上沿着不同方向色散，相机采集的多帧空间—光谱复用数据通过算法重建高光谱图像。

下面将讨论运用压缩感知理论来实现利用少量几个DVP旋转角度下的观测来重建高光谱图像的欠定重建问题。

1.连续模型

图5－6中的物镜将观测场景成像于视场光阑处，记各波长光谱图像为f（x，y，λ）。为简便起见，设后续光学系统的径向放大倍率为1，则FPA上的复用图像与视场光阑处拥有相同的空间坐标系。f（x，y，λ）经过透过率函数为t（x，y）的编码模板后被DVP偏移，其在FPA上的偏移量为

式中，k＝dl／dλ为光谱仪线色散系数，由焦距与DVP色散系数决定；λ0为中心波长；ϕ∈［0，2π］为DVP的转动角度。

当DVP绕光轴的旋转角为ϕ时，点（x，y）在光谱—图像立方体中的色散分布位置如图5－7所示。可见，点（x，y）在色散后将分布于色散线D上，而积分线I上的点色散后的空间坐标将均为（x，y）。积分线I通过三维空间中的（x，y，λ0）和（x－kcosϕ，y-ksinϕ，λ0＋1），与λ轴（即为光轴）夹角为因此，f（x，y，λ）沿着I的线积分就是FPA上所有入射到（x，y）点的光谱维积分。

式中，Λλ为探测器光谱响应范围，此处暂不考虑探测器光谱响应函数的影响。

图5－7　CTHIS色散模型

注：DVP转角ϕ为π时，不同波长平面上点（x，y）将在ϕ方向上获得Δs（λ）的偏移量，所有色散点将分布于直线D上；同理，所有位于积分线I上的点色散后的空间坐标均为（x，y）。

则式（5－5）的二维空间CFT为

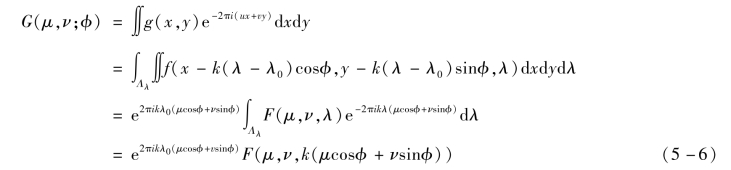
式中，F（·，·，λ）为λ波长图像f（x，y；λ）的二维CFT；F（·，·，·）为f（x，y，λ）的三维CFT。

可见，光谱—图像立方体沿着积分线I的投影在频率域中确定了F在ω＝kcosϕ·μ＋k sinϕ·ν平面上的值。但由于式（5－6）中相移因子的存在，G（μ，ν；ϕ）与λ轴的夹角并不为α，这在文献［147］中有详细的描述，如图5－8所示。(www.xing528.com)

图5－8　光谱层析与X射线变换数据采集的几何关系

2.离散模型

为进行数字计算，分别以Δx、Δy和Δλ对三维连续分布f（x，y，λ）无混叠采样，得到数据立方体f（m，n，l），－Nx／2≤m＜Nx／2－1，－Ny／2≤n＜Ny／2－1，－Nλ／2≤l＜Nλ／2－1。不失一般性，假定像元间距Δx＝Δy＝Δ，这相当于在频域中采样。

注意，上式中最后一个等号用到了色散系数k＝Δ／Δλ，即隐含着相邻谱段光谱图像在探测器上色散距离为1个像素。由式（5－7）有

并注意到中心波长λ0的索引n0＝0，则连续光谱层析成像模型式（5－6）的离散化形式为

这给出了层析光谱成像在傅里叶域中的采样位置。为快速计算，将光谱维频率索引向其最邻近整数网格点圆整

图5－9给出了切片数分别为4和5时，三维傅里叶域中的采样分布。

图5－9　三维傅里叶域中的层析采样分布

（a）零频率在立方体左上角，与MATLAB中的FFT相对应；（b）零频率在中心，与fftshift相对应

将所有测量噪声建模为高斯白噪声，则式（5－8）的矩阵—向量形式为

式中，为由f（m，n，l）顺序排列而成的原始数据向量，为三维傅里叶变换矩阵；为选择矩阵，由N阶单位矩阵中的M≪N行构成；n∈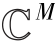为复高斯噪声。从非相干抽样的角度看，测量矩阵P对应的标准正交基IN与Fourier基F不相干，因此虽然P的行向量并非完全随机地从IN中抽取，但三维傅里叶域中的层析抽样对于频谱稀疏数据仍然是一种好的CS测量方法［131，161］。下面给出成像光谱数据在三维稀疏性约束下的快速频域重建算法。