Hadamard组合测量编码在高光谱成像中的应用探索

成像光谱仪采集观测场景的空间—光谱亮度分布，生成由两个空间维（x，y）和一个光谱维（λ）表征的三维数据集，称为光谱数据立方体。虽然目前有少量多光谱成像仪可采用三维探测器［132，133］，但是绝大多数光谱成像技术利用一个二维（或一维）探测器阵列采集三维光谱数据，因此传统成像光谱仪需要在空间维（摆扫型和推扫型［134］）或光谱维（滤光型［135］和干涉型［136］）扫描以获得完整数据立方体。这一用二维探测器直接测量三维数据的维度失配将引起单个光谱通道的SNR不足和全体数据采集时间过长问题，尤其限制了动态成像光谱测量的可用性。为此，新型光谱成像技术从无狭缝设计和复用测量等环节入手，研究获得信号优势（Signal Advantage［137］）和瞬态优势（Snapshot Advantage［123］）的新方法；这与20世纪50年代傅里叶变换光谱仪获得的通量优势（Throughput or Jacquinot Advantage［138］）和复用优势（Mul⁃tiplex or Fellgett Advantage［139］）一样，使得预期的信号采集能力可比狭缝—色散型成像光谱仪提高两个数量级以上［137，140］。

虽然复用采集可以获得更高的信号采集能力，但是测量信号并不以原始光谱数据立方体中的体素形态呈现，从而光学复用—数字解复用方法便构成了计算光谱成像的核心研究内容：优化选择复用体素的组合方式、复用过程的光学系统实现、解复用（重建）算法。复用成像光谱仪的两种主要复用方式包括层析复用和Hadamard复用。

层析复用的两个典型应用方式是CTHIS［140］和CTIS（Coputed－Tomographic Imaging Spec⁃trometer）［126］，二者的区别在于是否采用高阶色散元件。CTHIS用一个直视棱镜（Direct－View Prism，DVP）完成色散，探测器接收到原始数据立方体沿与光谱轴成一锐角方向的投影；而CTIS采用二维色散光栅实现二维高阶色散，探测器在不同区域上接收到原始数据立方体沿不同方向上的投影。色散方式的不同决定了在相同空间分辨率约束下，CTHIS适用于宽视场遥感应用［141，142］（重建的光谱图像尺寸仅略小于探测器阵列规模，但需要在多个DVP旋转角度下采集数据来完成光谱数据立方体的过定重建），而CTIS则更适于窄视场的瞬态光谱成像［143，144］（高阶色散将重建图像尺寸限制为探测器阵列规模的若干分之一，但探测器单个积分周期内的数据采集即满足重建需要）。两种层析复用与其他有限角下的三维层析重建一样，如X光CT、MRI（Magnetic Resonance Imaging）、PET（Positron Emission Tomo⁃graphy）、SAR（Synthetic Apture Radar）等，均是通过中心切片定理来关联物空间的二维层析投影和Fourier域中的一个过原点切片［145］，因此都面临着傅里叶域中的“丢失锥”问题，需要由后处理算法估计出未采样区域中的频谱分布［146，147］。

Hadamard复用的组合测量编码采用Hadamard矩阵结构，在应对探测器加性噪声方面是最优的［148］。Riesenberg和Dillner采用DMA（Digital Micro－mirror Array）来实现Hadamard编码［149］，每次采集时通过改变微镜的不同朝向获得序列观测用于重建。Brady等［150］则应用一个固定Hadamard编码模板的线性位移来实现多次观测和重建。为获得高光谱感知与处理一体化的能力，Muise和Mahalanobis利用目标识别结果来驱动DMA的Hadamard编码方式，获得了变分辨率高光谱成像［151］。Hadamard复用光谱成像没有层析复用方式的“丢失锥”问题，因此重建的数据立方体有较高的分辨率，但是其总体通量约为50%，从而测量信号强度要比层析成像低一半。

从求解线性系统方程的角度，为了获得唯一重建结果，要求测量数据量不得小于信号元素总数。然而近年来建立的压缩感知CS理论［131，152，153］则为数据采集和重建提供了全新视角：如果一个信号x∈Rn在某个正交基Ψ＝［ψ1，…，ψN］下是K稀疏的（α＝ΨTx最多有K个非零分量），或者是可压缩的（‖αK－α‖2很小，αK仅包含α中的K个最大分量），则可以通过求解以下形式的凸优化问题，以高概率从投影测量y＝Φx中精确地恢复出x。

式中，l1范数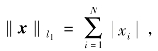总变分Φ为M×N的测量矩阵。式（5－1）和式（5－2）均有利于信号的稀疏性重建，但式（5－2）的实际应用效果通常好于式（5－1）。

利用式（5－1）或式（5－2）重建x的精度和所需的测量数量K由Φ的RIP（Restrict⁃ed Isometry Property［154］）或者非相干性（Incoherence［155］）决定，它们直观上都表征着Φ将x中蕴含的信息扩展和分散到不同测量数据中的能力。CS的理论框架［153，156，157］及其在成像领域中的应用［158，159］已有多篇文献予以介绍，本章从测量矩阵Φ的实现方法角度，回顾并比较CS理论在高光谱成像中的应用情况。

虽然近期提出了一些新的CS测量矩阵的设计方法［160－163］，但测量矩阵Φ的常用测量策略主要有三种，其中随机性均起到了关键性作用：（1）概率抽样［152，164］：Φ中的每个元素Φij从正态分布N（0，1／M）或二项分布＝1／2中独立抽样。如果x在某个正交基Ψ下是K稀疏的，则由M～O（K·log（N／K））次测量可确切重建(www.xing528.com)

（2）非相干测量［131，165］：从一个N×N的单位正交矩阵U（如FFT、DCT矩阵）中均匀随机地抽取M行并逐列归一化后构成Φ。此时，确切重建x所需的测量次数M＝O（μ2·K·logN）取决于Φ与Ψ之间的“互相干”性［166，167］。

当μ＝1时，Φ与Ψ不相干，此时Φ与Ψ有最小的相似性，Ψ的每个元素都会“平摊”到Φ空间中，从而有更多的机会在每次测量中都保留有x的信息。（3）随机卷积［168］：Φ由随机脉冲卷积和下采样两步构成。首先构造卷积矩阵H＝F∗ΣF，其中F为DFT矩阵，由具有随机相位的单位复数序列σ1，…，σN构成其对角线元素。从H中随机抽取M行构成Φ，或者将H中每N／M行随机调制求和构成，相应的所需测量次数分别为M～O（K·logN）和M～O（K·log2N）。

上述CS的重要结果在理论上阐明：有可能通过远少于光谱数据立方体体素数N的M次随机测量（M～O（K·logN）≪N）来重建出原始光谱图像，这对于提升成像光谱仪的数据采集效率和SNR具有重要意义，因此近年来吸引研究人员开展了众多研究工作。从成像光谱仪实现随机测量的方法来看，绝大多数基于CS的光谱成像技术采用的是“概率抽样”策略来实现随机测量，其中最为著名的是杜克大学的Brady研究组的CASSI［128－130，169－171］，通过一个静态二值编码孔径和单［169］或双［128］色散元件来调制光场，并利用探测器采集到的单个二维投影来重建出三维数据立方体。为提高重建精度，他们随后利用多个二维投影来降低数据重建的病态性［170，171］。而Arce的研究组则利用一个DMD器件在多帧采样时对孔径动态编码［172］，实现了敏捷光谱成像［173－175］——光谱和空间分辨率可调节，或者只复原感兴趣谱段的光谱图像。

与上述CASSI采用的单个随机编码孔径实现局部空间上的光谱复用不同，Arce研究组提出了基于随机卷积的瞬态光谱成像方法［176］，首先利用傅里叶变换透镜和空间光调制器对空间光场进行随机卷积，实际上是将二维空间信息充分地混合“散布”到每一个探测器上，并通过色散元件实现整体空间上的光谱复用。这种全局复用使得在每一个测量数据中都蕴含着原始光谱数据立方体的大部分信息，更利于捕获任意稀疏结构［177］，因此其光谱图像重建效果要优于CASSI。但是利用傅里叶光学实现频域滤波的方案只适用于相干光照明的情况，限制了其在非相干照明环境下的应用。

本节提出了压缩光谱层析成像方法，其主要贡献在于：

（1）由光谱数据立方体中部分三维傅里叶系数（所在位置由中心切片定理确定［145］）重建光谱影像，相对于CASSI测量模型具有更低的互相干性和更高的全局复用性，故更有利于高空间和高光谱分辨率的稀疏重建。

（2）给出了基于FFT的逐点运算快速算法，无须显示构造系统方程矩阵，这一计算优势确定了本章方法对于高光谱影像重建的实用性。