自适应、随机和全体样本选择的重建效果比较

样本的数量和多样性对基于学习的超分辨率重建的结果有很大影响，但是否样本数量越多重建效果就越好呢？是否有可能用相对少量的样本就能获得较好的重建效果呢？在这个实验中，分别使用了基于LPP的自适应选择样本、随机选择样本和全体样本，图4－9为重建效果的比较。首先统计出使用本章提出的自适应样本选择方法所选择出的平均样本数，再随机选择出相同数量的样本完成重建，最后使用所有样本。

关于这三种样本选择方法的一些统计数据^[2]列于表4－1中，其中包括每个像素块（12×12）的PCA子空间的平均维数（所选最大特征值之和占全部特征值和的99.99%）。

从图4－9和表4－1可以看出，本章提出的LPP样本选择方法的重建效果明显好于随机样本的重建效果，而与使用全体样本的结果几乎相同，但计算时间减少近55%。这里需要指出以下两点。

图4－7　局部重建与全局重建比较

（a）低分辨率图像；（b）图（a）的BiCubic插值；（c）全局重建；（d）本章算法；（e）原始高分辨率图像

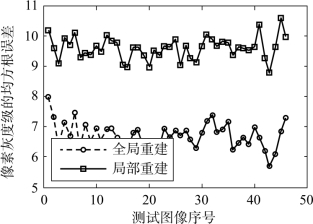
图4－8　文献［41］的全局重建与本章的局部重建图像的均方根误差

(www.xing528.com)

图4－9　不同样本选择方法的重建效果比较

（a）低分辨率图像；（b）图（a）的BiCubic插值；（c）随机样本；（d）自适应样本；（e）全体样本；（f）原始高分辨率图像

表4－1　三种样本选择方法的平均重建时间与平均RMSE

（1）自适应样本选择方法中LPP系数的平均长度仅为6.7，因此对LPP系数的最邻近搜索只占像素块重建运算的很小一部分。

（2）在拥有大量样本时（如5 000张人脸图像以上），自适应样本选择方法会显示出更大的优势，因为总是可以动态地选择出适当数量的最相似样本用于重建，而如果使用全体样本，这种大规模样本的学习只能使用Iterative Kernel PCA［43］等方法离线计算，这显然就丧失了自适应样本选择的能力。

在图4－7和图4－9的最后一行，还给出了两个戴眼镜的低分辨率人脸的超分辨率重建结果，虽然从低分辨率人脸中很难辨认出眼镜的存在，但是本章的算法还是能合成出比较接近于原始图像的结果，而对于其他没戴眼镜的低分辨率测试图像，并没有错误地添加上眼镜，这与全局图像重建和使用随机样本的重建结果所带来的“眼镜效应”明显不同，也又一次体现出了自适应样本选择的优势。需要进一步指出的是，本章的算法是根据低分辨率输入图像来忠实地恢复出眼镜（如果在原始高分辨率图像中确实存在），这与文献［41，53］中使用全部戴眼镜的人脸训练图像来为不戴眼镜的输入图像“添加”上眼镜的例子有本质不同，本书的方法能够更为客观地根据输入的低分辨率图像来重构出其高分辨率版本。

这个实验证实：本章使用的基于LPP的自适应样本选择方法可以通过有效地选择出相对少量的样本来获得很好的超分辨率重建结果。