相关工作：图像SR中的Tikhonov规整化及亚像素级精确运动估计

图像的超分辨率是指从多张低分辨率（通常也是低质量的）观测图像中融合出具有更高光学分辨率图像（或序列）的信号处理技术。1984年，通过利用DFT的位移与混叠性质，Tsai和Huang提出了从一个彼此间存在亚像素平移运动的低分辨率图像序列中提高图像分辨率的频域方法［93］，他们的开创性研究突破了当时人们对于信号和图像的分辨率增强方法的认识局限——在此之前普遍认为提高图像分辨率最好的方法是三次样条插值。此后至今的30多年中，SR一直是一个非常活跃的研究领域，文献［94－96］从不同的角度对已有SR方法做了综述和展望。这些方法通常是基于“重建约束”的，而最近10年出现的基于学习的SR［36］则通过样本学习为高—低分辨率图像对建立一个共生模型，进而为低分辨率图像“添加”出高频细节。这类方法通常适用于某个特定图像类的SR问题，如人脸图像［33，40］。

由于成像过程中的模糊过程可以建模为一个紧支撑的模糊核与图像的卷积（属于第一类Fredholm积分方程），因此，SR重建是一个病态逆问题。作为最早的规整化方法，Tik⁃honov规整化在图像的SR中仍然得到广泛应用。Nguyen等［60］应用块循环的PCG方法迭代求解SR问题。由于循环矩阵可以被DFT对角化，故线性系统的求解都通过FFT高效完成。虽然Tikhonov规整化使SR在矩阵分析与数值计算方面较为便捷，但是它全局化的平滑性约束将模糊图像边缘等高频细节。近年来对SR中规整化项的一些新的尝试主要体现在以下两方面：

（1）采用非二次的Lp范数规整化惩罚函数（1≤p＜2）来约束图像其他方面的性质，如Daubechies等［97］用加权Lp范数来对信号在特定基下的稀疏性（分解）进行约束，而Far⁃siu等则应用图像的双向全变差（Bilateral Total Variation）的L1范数来保留图像的尖锐边缘和点状细节［81，98］。

（2）采用其他的规整化算子来探求对图像先验知识的更为精细的刻画，如Woods等使用高斯SAR（Simultaneously Auto Regressive）固定先验模型来将像素灰度值建模为一个高斯随机过程，而基于全变差的规整化由于在局部邻域内考虑灰度值的变化，因此能更为完好地保存图像的边缘细节［71，81，98］。

在文献［69］中，Chantas等提出了一个图像先验的双级模型，用高斯分布定义在水平和竖直方向上图像的局部边缘结构的概率分布，并用一个伽马分布来描述高斯分布中每个像素位置上的方差参数的致信度，从而实现了自动调节的图像先验分布，该方法的优点在于在保留图像边缘的同时压制了“振铃”效应。(www.xing528.com)

上述规整化方法的共同特点是力求用一个简单的数学表达式来显式地定义出图像分布的概率密度函数，然而众多SR实践表明，这种出于直观思考的简单数学表达式并不能充分定义图像丰富多变的内容，尤其是图像邻域上的各向异性行为，但重建出这些局部的细微变化恰恰是SR的主要目的。最近关于更好地定义图像先验的一种思考是：通过学习的方法，从样本中获取图像各种更为复杂的先验描述，即基于样本的规整化［99］。本章提出一种新的基于学习的特征子空间人脸图像规整化方法，基本思想是：人脸图像作为一个特定图像类别，适合于用学习的方法提取其主要特征；另一方面，由于人脸有很强的结构化特征，这种局部相关性（马尔科夫性，被广泛用于图像处理领域，如文献［36］）允许独立地分析和处理人脸上的每一个图像块，而且文献［100］也表明，基于块的学习有更高的效率。基于以上两点，我们将人脸图像上每一个q×q大小的块看作一个q2维信号s∈V⊂H，此处V为Hilbert空间H中的K维信号子空间（1≤K＜q2）。如果能够完全确定V的一组正交基则可以得到s在下的唯一表示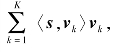但是当通过学习的方法（如PCA）获得V的一个估计V＾时，由于样本规模的限制往往V＾⊂V。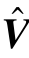为了保留s的多样性，我们约束s在V＾的正交补空间U上投影的大小为，从而约束SR的结果不至于离太“远”。

SR中的另外一项关键任务是亚像素级的精确运动估计（图像配准）。由于成像系统中传感器的像元尺寸、填充系数及模—数转换频率的限制，光学镜头的衍射极限通常远高于传感器对应的Nyquist采样频率，从而引起数字图像的频谱混叠。正是由于混叠的存在使得早期的“先配准再重建”的两段式SR结果并不理想：Irani等［25］用基于梯度的方法［101］配准LR图像对，然而这些混叠图像显然不满足该类方法对图像灰度保持不变的假设。Capel等用RANSAC方法［102］配准图像［103］，但从模糊的小尺寸LR图像中找到大量特征点本身就很困难。另一种SR方法是把图像配准和图像融合（及去模糊）纳入一个共同的过程中进行联合估计［20，66，68－71］。Hardie等首先考虑了配准与重建的联合估计问题［20］，用循环坐标下降（Cyclic Coordinate Descent，CCD）方法交替优化配准参数与HR图像。但是这种方法不能保证算法的全局收敛性［104］。文献［70］中给出了一种基于EM算法的交替求解方法，在E－步估计HR图像，在M－步估计未知参数，但两部分都需要比较精确的初始估计。将SR重建看作一个可分离非线性最小二乘问题［104］，Robinson等［66］首先通过变量投影函数的最优化得到运动参数的估计，再利用该参数得到HR图像的ML和MAP估计。文章中给出了频域中的快速算法。在文献［93］的基础上，Vandewalle等提出了两种基于子空间的频域配准与重建方法［68］，但是其系统方程中没有考虑图像的模糊问题。以上SR方法的一个共同局限是将运动模型限制为纯平移，这个假设的一个最大的好处是：全局平移对应一个块循环矩阵，因此SR在空间域中的大规模稀疏矩阵求逆问题便可以转化为频域中的对角矩阵求逆。Chantas等［69］考虑了旋转—平移的运动模型，但仍然是首先通过LR图像配准获得旋转参数的估计，然后在频域内估计平移参数。

最近关于更复杂运动模型的SR方法是：利用局部四邻域双线性插值方法，推导出HR图像关于运动参数的Jacobi矩阵，再通过泰勒一阶展开［71］或二阶展开［83］将非线性的SR问题转换为线性问题迭代求解（最常用的非线性问题求解方法）。本章在仿射变换运动模型下，将图像的四邻域插值方法拓展为图像的梯度场估计问题，导出了更一般形式的Jacobi矩阵，并且根据对SR代价函数的全微分和偏微分展开，给出了三种运动参数与HR图像的联合迭代估计算法。