【摘要】：然而真正的计算负荷在于Null的确定，因为Y的大小为，即使～，Ye＝0的直接求解也是相当困难的。仍然通过最小二乘法来确定Null：对大小的YTY做谱分解，其R个最小特征值对应的特征向量即张成Null。显然，首先，可以发现［C｛Yk｝］T的结构与式（2－6）中的有效卷积矩阵是相同的，只不过各列的次序发生了颠倒：则由式～式知：这样，Λmn的计算可以通过在Ym与Yn的互相关矩阵Yn中按式截取不同位置上的me×ne大小的块来得到。
式（2－30）中N的大小为（R（mh＋me－1）（nh＋ne－1），Kmhnh），因此对于一般尺寸的模糊核（如10×10），式（2－32）中的NTN将只是一般规模（约103×103）的矩阵计算问题，即使用奇异值分解也可以求解式（2－32）。然而真正的计算负荷在于Null（Y）的确定，因为Y的大小为（（my＋me－1）（ny＋ne－1），Kmene），即使（my，ny）～（100×100），Ye＝0的直接求解也是相当困难的。仍然通过最小二乘法来确定Null（Y）：对（Kmene，Kmene）大小的YTY做谱分解，其R个最小特征值对应的特征向量即张成Null（Y）。
下面通过考察Y的特殊结构来简化RY＝YTY的计算，这种思想也见于文献［92］中。显然，
首先，可以发现［C（me，ne）｛Yk｝］T的结构与式（2－6）中的有效卷积矩阵是相同的，只不过各列的次序发生了颠倒（各子矩阵也是如此）：(www.xing528.com)
则由式（2－34）～式（2－36）知：
这样，Λmn的计算可以通过在Ym与Yn的互相关矩阵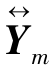
∗Yn中按式（2－37）截取不同位置上的me×ne大小的块来得到。直接计算RY需要
次乘法，而利用FFT（Fast Fourier Transform）按照式（2－37）计算RY的计算复杂度是O（K2mynylog（myny））。使用这种方法甚至无须构造卷积矩阵C（me，ne）｛Yk｝。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
