离散化观察模型的方法

下面讨论观察模型的离散化，以便在计算机上进行数值计算。

对f（x）、h（x）均在像平面P上以间距Δ′均匀采样，假设Δ′≪ΔNyquist，而ΔNyquist为Nyquist采样距离，即

则f（x）、h（x）均可由其离散采样f［i］、h［i］精确重建，即

式中，φ（x）为一个核函数，可以为任何经典的插值核（如box、bilinear及bspline函数等），φ（x）的一组平移函数构成了2上的一个基。

定理2：对于式（2－10）中定义的仿射形变算子W（·），定义f（x）的一个测度为其支撑Df的面积，即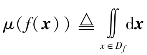，则

证明：对于f（x）与W（f）（u），由式（2－10）知u＝（x），故

注：DW（f）为图像形变后的支撑。

定理2表明：当时，f（x）被放大；当时，f（x）被缩小。

推论2：假设f［i］＝DΔ′（f（x））可以精确重建f（x），如果以Δ′为间距对f（x）采样不会造成混叠，那么以Δ′为间距对W（f）（x）采样也不会造成混叠。

证明：假设以Δ′为间距对f（x）采样能够得到P个采样点，则由定理2知以Δ′为间距对W（f）（x）采样能够得到P个采样点，如果，这相当于对f（x）做倍的下采样（在水平和竖直两个方向上），如果能够保证ΔNyquist，则由采样定理知不会造成混叠。

由式（2－8）与式（2－15）知(www.xing528.com)

W（f）（x）＝仍然对W（f）（x）按Δ′为间距采样，

则

其矩阵—向量形式为

而式（2－9）可以写作

式中，D为二维s∈倍下采样矩阵；C（mf，nf）｛H｝为由H构造的卷积矩阵。

由推论2可知，若min｛Δ′，Δ′／则可以通过f［i］和fW［i］分别精确重建f（x）和W（f）（x）。

进一步地，假设有K张LR图像，如果max而且，1≤k≤K，那么以Δ′为间隔对f（x）、W（f）（x）及W－1（f）（x）均匀采样都不会引起混叠问题。显然，通过选择中有最高空间分辨率的一帧来作为参考图像，即可达到上述要求。此时，可令则Δ＝sΔ′。事实上，一个连续图像序列之中，相邻几帧之间的尺度变化不会太大，即

难以避免的混叠出现在g［p］＝DΔ（［h∗W（f）］（x）），或等价式（2－13）之中，因为因此，以Δ′对推论1中定义的g（x）均匀采样，即式（2－13）会产生混叠。但是，由于h（x）对W（f）（x）的模糊作用，使W（f）（x）中的高频成分损失了一部分，故当下采样倍数较小时，可以认为g［p］可以近似重建g（x），即

由此，式（2－14）的矩阵向量形式可写作

式中，及W－1分别为（x）和W－1（h）（x）对应的形变矩阵，它们都是图像的插值运算；C（mh，nh）｛F｝为由F构造的卷积矩阵。