正确选择观察模型：SRR任务中的仿射变换模型

一个合理的观察模型应该能够正确地抽象出成像的实际物理过程。在超分辨率领域中，成像过程目前被普遍认可的三个阶段包括形变、模糊与下采样。

形变的产生来自场景与成像设备间的相对运动，根据运动的复杂程度，可以选择纯平移［20，66，81，82］、刚体运动［69，71］、仿射变换［27，83］、单映［26，84］或光流［85］来对其建模，然而，所有形变模型都是以BCA（Brightness Constancy Assumption）为基础的［86］。

引起模糊的因素比较多，比如：如果观察场景与成像设备之间的相对运动较快，以至于在快门时间（生成一帧图像的积分时间）之内，这个相对运动在像平面上超过一个像素间距就会产生运动模糊；光线从场景传播到成像设备之间的大气扰动，严格来讲会产生各向异性，即空间变化的模糊；光学镜头本身的PSF（Point Spread Function）及散焦也必然会产生成像模糊。基本上，可以将所有模糊的整体效果抽象为一个空间移不变模糊，因为这在基本不影响问题本质的同时给数学处理方法提供了极大便利。

下采样实际上是一个二维采样过程，只是由于采样间隔大于Nyquist采样定理的要求而产生了混叠，相对于无混叠采样称之为下采样。SRR的基本任务就是从混叠的LR图像序列重建出一幅无混叠或至少混叠程度大为降低的HR图像。绝大部分SRR方法都是考虑的整数倍下采样，但也有一些基于Polyphase的工作讨论了有理数倍下采样［80，87］。

观察模型时的一个重要问题是形变与模糊的发生次序。如果光学系统模糊占据整体模糊效果的主要部分，则可以认为模糊发生在形变之后，即形变—模糊；若大气扰动是模糊的主要来源，则可认为模糊发生在形变之前，即模糊—形变［88］。根据这个原则，一些遥感应用中的模糊主要来自长距离的大气扰动，因此采用模糊—形变次序［84，89－91］，而其他大部分可见光谱段的SRR方法则均选择形变—模糊次序来建模。

本章工作的目的是利用摄像机视频来重建出感兴趣区域的HR图像。当摄像机固定且光轴与其观察的平面场景垂直时，仿射变换可以准确地描述图像序列之间的平移、旋转、缩放及切变（Shear），并且当摄像机的摇角不大时，仿射变换也足以精确地近似投影变换。因此，一个序列中相邻几帧图像中的感兴趣区域，如人脸、车牌等，大多可以用仿射变换来描述其相对运动关系。本章的工作即选择仿射变换模型。(www.xing528.com)

综上所述，连续强度函数f（x）在经过几何形变、空间移不变模糊图像传感器离散化后，将得到LR图像g［p］，p∈GΔ。这一过程可以写作

式中，h（x）为模糊函数；s↓表示s倍下采样；n（x）为加性成像噪声，这里假设为i.i.d高斯白噪声；W（·）为2.2节中定义的形变算子，W（f）（x）≜f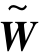（－1（x）），其几何变换为仿射变换，即

式中，M为关于坐标x的2×2线性变换矩阵，x∈p；d为2×1平移向量。

下面首先讨论在连续坐标系统下，式（2－9）在无噪声情况下的一种等价形式，然后讨论其对应的离散模型。