如何定义一维和二维卷积矩阵

本书中小写黑体字母代表向量（如无特别说明，向量均指列向量），大写黑体字母代表矩阵。所有问题都在像平面上讨论，为其赋予直角坐标系（x，y）。感兴趣场景以其在像平面上的光强场f（x）来描述，其中x＝（x，y）T∈Z2表示像平面上的连续位置，而以p＝［p1，p2］T∈Z2与i＝［i1，i2］T∈Z2分别代表LR图像网格GΔ与HR图像网格GΔ′上像素的离散位置（Δ′与Δ分别表示GΔ′与GΔ的采样间距）。一个图像既可以通过连续场f（x）描述，又可以通过二维离散序列f［i］表达（大小为（mf，nf）），而其对应的矩阵F逐列排列后的向量写作f，即f≜vec｛F｝，F≜Unvec（mf）｛f｝表示电向量f重新构成二维矩阵。

一个向量f＝［f0，…，fmf－1］T的长度记为mf，f（ma：mb）≜［fma，…，fmb］T；而矩阵H的大小记作（mh，nh），H（ma：mb，na：nb）≜H［ma：mb，na：nb］代表H从（ma：mb）到（na：nb）的子块。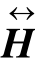代表H的坐标反转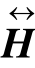，［i，j］≜H［mh－i－1，nh－j－1］。

下面定义一维与二维卷积矩阵的形式。

向量f与h的卷积为z，长为mf＋mh－1，即z＝f∗h＝Cmf｛h｝f，其中Cmf｛h｝为（mf＋mh－1，mf）的Toeplitz矩阵：

注意，这里的Cmf｛h｝并不是通常定义下的方形Toeplitz矩阵，其对应线性卷积运算。事实上，Cmf｛h｝的每一列都是h补零后的循环移位。以（mb－ma＋1，mf）Toeplitz矩阵｛h｝代表Cmf｛h｝的ma到mb行构成的子矩阵，有有如下形式：

式中，ht取0时对应于t＜0和t＞mh－1。因此，仍然是带状矩阵。

图像F与H的卷积为Z，大小为（mf＋mh－1，nf＋nh－1），Z＝F∗H的矩阵—向量形式可写作(www.xing528.com)

式中，z≜vec｛Z｝；f≜vec｛F｝；H＝［h0，…，hnh－1］；C（mf，nf）｛H｝是（（mf＋mh－1）（nf＋nh－1），mfnf）的TBT（Toeplitz－Block－Toeplitz）矩阵，定义为

C（mf，nf）｛H｝中有nf＋nh－1个行块，nf个列块，其每一个行块完成H与F某一列的卷积。定义（（mb－ma＋1）（nb－na＋1），mfnf）的TBT矩阵，使得vec｛（H∗即

式中，取O对应于t＜0或t＞nh－1。如果取ma＝mh－1，mb＝mf－1，na＝nh－1，nb＝nf－1，则有

式中，

对图像f（x）的形变算子W（·）定义如下：

式中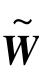，（x）与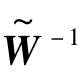（x）分别代表像素坐标的几何变换及其逆变换，x∈P，P为像平面。