学习方法优化：基于实践的建议

虽然在理论上基于重建约束的方法有着信号处理和估计理论等方面的有力支撑，但是随着放大系数的增加，这些方法生成的HR图像中包含的高频信息将越来越少［33］。近年来，由于在高倍放大系数（4～16）下具备更强的高频信息恢复能力，基于学习的超分辨率方法受到研究人员的广泛关注。在基于学习的SR方法中，Baker等的工作［34］给其他学者的研究带来了很大启示。

1.Face Hallucination

Baker等［33，34］提出了一种专用于人脸图像的超分辨率方法——Face Hallucination，通过利用以金字塔形式组织的正面人脸图像的梯度分布先验，在最大后验概率的框架下完成超分辨率重建。由于重建过程是逐像素进行的，因此容易缺失一些人脸的全局性约束，如对称性和亮度的一致性等。值得指出的是，他们在定义HR图像的先验分布时，使用的是从训练人脸库中搜索出的最相似像素的水平和竖直梯度，而不是简单地为所有HR图像定义一个完全相同的先验分布（如基于重建约束方法中的Gibbs分布等），这就使HR图像的先验项是与输入的LR图像相关的，即基于识别的梯度先验。对HR的估计是通过梯度下降算法完成的。

2.Image Analogies

Hertzmann等的图像类推［35］（Image Analogies）也是一种基于样本的图像处理方法，分为两个阶段：在“设计”阶段，需要提供一个图像对作为训练数据，其中一幅被看作另一幅的滤波版本；在“应用”阶段，从设计阶段中学习到的滤波器被运用到新的图像上，从而得到一个相似的滤波结果。图像类推实际上是基于一个多尺度自回归模型。

3.基于马尔科夫网络的方法

Freeman等使用马尔科夫网络来学习图像的高频—低频信息之间的关系［36，37］。在设计训练图像库时，高分辨率图像经平滑和下采样得到对应的低分辨率图像，并通过三次样条插值将LR图像放大为HR图像的尺寸。分块提取LR－HR图像中的高频数据，并用LR图像的局部均值对这些图像的高频数据做归一化，这样可以减少需要存储的样本数量。在SR重建时，应用马尔科夫网络从概率的角度建模高—低分辨率图像块，以及相邻高分辨率图像块之间的关系，其模型如图1－3所示。

图1－3　超分辨率的马尔科夫网络模型

该模型可以用数学公式表达为

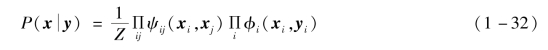
式中，y为输入的LR图像；x为待估计的HR图像；xi，xj为HR图像中的局部相邻块；yi为与xi对应的LR图像块，这些图像块表示图1－3中的节点；相容性函数ψij关联着相邻隐含节点的可能状态；ϕi则关联着每个观察节点和对应的隐含节点之间的状态。

马尔科夫网络的计算量是比较大的。

4.基于特征脸子空间的方法(www.xing528.com)

Gunturk等［38］提出了在特征脸子空间中同时进行人脸图像超分辨率重建与识别的方法。在图像空间和特征脸子空间中，观察模型可以分别表达为

式中，Ψ和Φ分别为LR与HR特征脸子空间的特征向量矩阵；a＾k与a分别为LR与HR人脸图像的投影向量；ex和nk分别为特征脸子空间的建模误差和观察噪声，被建模为一个总的高斯噪声Vk＝Hkex＋nk。

在MAP框架下，估计HR人脸图像x在特征子空间Φ上的投影为

式中，先验项P（a）和后验项P（，…，｜a）都被建模为高斯分布。

最后，使用梯度下降法优化求解a＾。

Liu等［39，40］提出了人脸超分辨率的两步法：首先，在特征脸子空间中，用一个全局参数模型根据低分辨率输入图像估计出高分辨率人脸图像；然后，用一个局部非参数马尔科夫网络模型来补偿第一步中重建的高分辨率图像与原始高分辨率图像间的残差。但是第一步中的全局参数模型需要已知降晰函数，而且第二步中的马尔科夫网络也需要复杂的计算。

Wang和Tang［41］提出了一种简单有效的单张LR人脸图像的特征变换超分辨率方法：认为LR图像和HR图像可以在各自的训练集合中用同一组系数作线性逼近。Chakrabarti等［42］应用Kernal PCA（Principle Component Analysis）来探索数据集中的高阶互相关，以此作为规整化超分辨率的先验知识。当样本集很大时，Kim等［43］提出使用Hebbian算法来计算Kernal PCA的迭代方法。

5.基于流形学习的方法

在维数约简技术中，PCA和LDA（Linear Discriminant Analysis）都属于特征向量方法，用于描述高维数据中的线性变化，当被用来揭示数据的欧氏结构时是有效的。但是，如果数据本身来自嵌入在高维嵌套空间中的一个低维非线性子流形，则上述方法就不能有效地揭示流形中蕴含的非线性结构，因此也就不适合这种情况下的探索性数据分析和模式聚类应用。最近几年，为探索流形上的非线性结构，人们提出了一些非线性技术，如Isomap［44］、Lapla⁃cian Eigenmap［45］、LLE［46］（Locally Linear Embedding）和LPP（Locality Preserving Projec⁃tion）［47］等。

近期的很多研究显示：不仅人脸图像位于一个嵌套在高维图像空间中的子流形上［48－50］，而且人脸图像的局部区域也可以通过流形学习的方法分析其内在结构特征［51，52］。

Chang等应用LLE来在高－低分辨率子流形上实现超分辨率［49］，而Zhuang等则使用LPP和RBF（Radial Basis Function）来实现人脸超分辨率重建［53］。