基于重建约束的优化方法

基于重建约束方法的超分辨率都是通过利用N张LR图像来重建出一张HR图像。通用的模型为

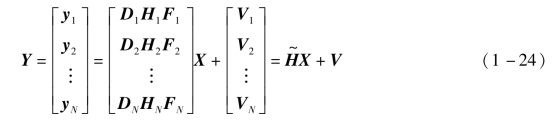
式中，yk是LR图像，k＝1，…，N；Hk＝DkHkFk代表成像系统；Vk为噪声，k＝1，…，N；X为HR图像。

1.非均匀插值法

非均匀插值的三个步骤如下：

（1）低分辨率图像配准，即运动估计。

（2）通过对配准后的低分辨率图像的非均匀插值［14，15］生成一张高分辨率图像。

（3）对生成的高分辨率图像去模糊。

该过程如图1－2所示。

非均匀插值方法的计算负荷较小，但是需要假定所有低分辨率图像的噪声和模糊特征都是相同的，而且在图像复原阶段忽略了插值阶段的误差。

图1－2　基于非均匀插值的超分辨率

2.频域法

在1.1.3节中已经回顾了Tsai和Huang的频域超分辨率方法［12］，以及Kim等对该方法的扩展［13］。后来通过使用Tikhonov规整化方法，Kim又对每张LR图像考虑了不同的模糊算子和噪声特性［16］。Bose等提出了使用递归总体最小二乘法来减轻配准误差影响的超分辨率方法［17］。通过使用离散余弦变换（Discrete Cosine Transform，DCT）而不是DFT，Rhee和Kang减少了运算量，并使用多通道自适应规整化参数来减轻问题的病态性［18］。

频域方法原理上简单，而且适于硬件的并行计算，但是只能采用全局平移运动模型和LSI（Linear Shift Invariant）模糊算子，而且由于频域数据缺少相关性，故空间域上的一些先验知识很难用于规整化。

3.规整化法

如果LR图像数量不能使方程组中的方程个数多于未知数个数，则式（1－24）是欠定的，此外模糊算子本身也是病态条件的，这使得超分辨率重建是个病态问题。为了稳定这个病态问题的逆过程所采取的措施称为规整化。

1）确定性规整化

确定性规整化超分辨率也是利用解的先验知识来使病态问题良态化，只不过利用了多张LR图像和更为复杂的系统模型。超分辨率的确定性规整化解可以通过以下的约束最小二乘问题得到［3］：

式中，高通算子C和规整化参数α的作用与图像复原式（1－8）中的作用是一样的。

由于使用了二次规整化项，式（1－25）是凸的且关于x可微，故其唯一解通过解如下方程得到：

2）随机规整化

随机规整化通常是在贝叶斯方法下，通过引入解的先验分布知识来规整化问题，常用的方法有最大后验概率（Maximum a Posteriori，MAP）法和极大似然（Maximum Likelihood，ML）法。(www.xing528.com)

设图像的先验分布为P（x），则MAP最优化可表示为如果使用Gibbs先验，则

式中，U（x）为能量函数；φc（x）为仅依赖于局部像素族的势函数；Z为归一化常量，并且假设各LR的系统误差和噪声是独立同分布（independent and identically distributed，i.i.d）零均值高斯分布，则式（1－27）可表示为

Schulz和Stevenson使用了具有边缘保持能力的Huber－Markov先验来完成超分辨率的MAP估计［19］，而Hardie等首先考虑了图像配准参数和HR图像的联合MAP估计问题［20］。

ML法可以看作没有先验知识的特殊MAP估计，但由于SRR问题本身是病态的，通常应优先选择MAP估计。Tom和Katsaggelos提出了同时估计LR图像的亚像素位移、噪声方差和HR图像的ML法，并通过EM算法求解［21］。

在建模噪声特性和图像先验知识方面，随机规整化方法有很强的鲁棒性和灵活性。

4.凸集投影法与极大似然－凸集投影法

Stark和Oskoui最早提出使用POCS来解决SRR问题的方法［22］。POCS是一种迭代求解法，同时解决HR图像的复原与插值问题。假设闭凸集Ci是满足某一特定属性的矢量集合，那么SR的解应该属于这些凸集的交集Cs可以通过依次向这些凸集投影得到，因此SR的POCS解由下式得到：

式中，Pi为形式化的到凸集Ci的投影算子，可以采用数据一致性约束和幅值约束等方法。

关于POCS的另一项重要工作是由Patti等完成的［23］。在他们的工作中考虑了空间变化模糊、非零快门时间、传感器像元的非零物理尺寸、传感器噪声及任意采样网格等问题。

POCS法原理简单，而且可以使用非常灵活的空间域观察模型，但是收敛速度慢，计算负荷大，且解不唯一。

文献［19，24］中通过最小化ML或MAP的代价函数，同时将解约束在某些凸集中来得到SRR估计，这样解是唯一的，而且可以有效地利用先验知识。

5.迭代反向投影法

迭代反向投影（Iterative Backward Projection，IBP）法最先由Irani和Peleg提出［25］。通过反向投影模拟LR图像和观察LR图像之差，HR图像由迭代方法得到。

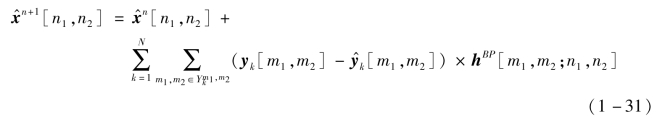
式中，有效像素集合取决于n1，n2∈x｝；hBP［m1，m2；n1，n2］是用于确定误差项对贡献因子的反向投影的核函数。

IBP法的优点是原理直观，而且可以考虑比较复杂的运动模型［26，27］，但是没有唯一解，而且在选择hBP时是困难的。

6.自适应滤波法

Elad和Feuer［28］提出了基于时间轴上的自适应滤波理论的SRR算法。通过修改观察模型来引入LR图像时间上的相关性，他们推导出了递归最小均方算法。每个时刻，HR图像都通过递归最速下降算法估计出，而且不需要计算矩阵的逆。这种方法适用于随时间与空间变化的模糊和复杂的运动，可以用于生成HR图像序列。后来，他们又通过对卡尔曼滤波器的逼近重新推导了递归最速下降和递归最小均方算法［29］。

7.利用非运动线索的超分辨率重建法

虽然大部分SR算法都需要用LR图像间的亚像素级运动估计，但是也存在利用其他非运动线索重建HR图像的方法，如应用MRF（Markov Random Field）模型［30］、光度学线索［31］和缩放线索等［32］。