如何计算带传动分析？实例分享

【实例1】 带轮轮槽与带的三种安装情况如图5-5所示，其中哪种情况是正确的？为什么？

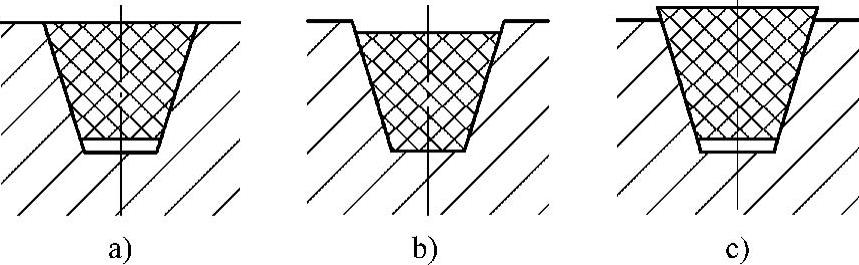
图5-5 实例1示意图

解：图a所示的情况是正确的，因为该安装情况相当于带和轮槽尺寸是按同一带的截面进行设计配置的，例如选用了A型带，则按A型带设计轮槽尺寸。图b所示的安装情况是带的截面积小于带轮，相当于带轮的轮槽尺寸大于相应带的尺寸，如采用A型带，而轮槽尺寸按B型带或C型带进行设计配置，因此带与轮槽底部接触，没靠侧面工作，相当于厚的平带，承载能力下降。图c所示的安装情况是带的截面积大于带轮，相当于带轮的轮槽尺寸小于相应带的尺寸，如采用B型带，而轮槽尺寸按A型带配置，虽然也能靠带的侧面工作，但是由于带不断啮入和脱开带轮，带的两侧面容易被金属带轮所磨损，降低了带的使用寿命。因此，图b和图c两种情况下带轮都不能正常工作，应该避免。

【实例2】 图5-6所示的两级减速装置方案，有什么问题？为什么？

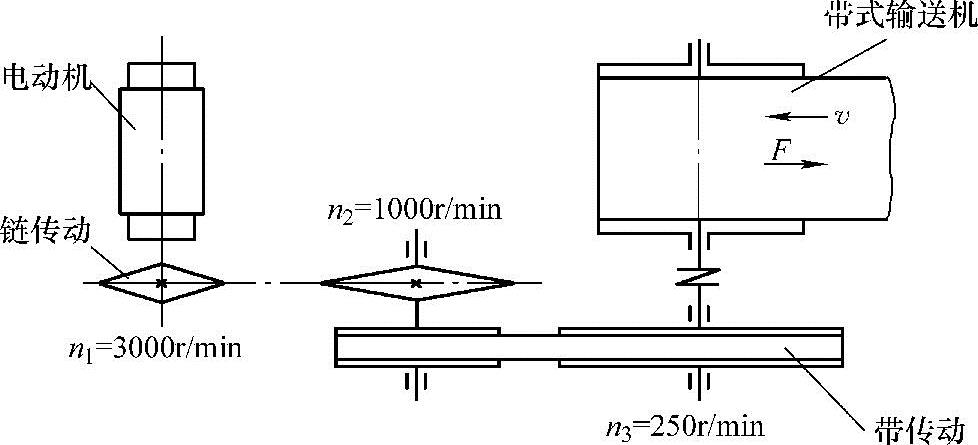
图5-6 实例2示意图

解：图5-6所示装置的问题在于带传动的位置错误。带传动应该布置在高速级，直接与电动机连接，一方面起到过载保护的作用，另一方面带传动中单根带所传递的功率与带的速度成正比，带传动在高速级，速度高，单根带所传递的功率大，所需带的根数少，可以节约制造带轮的材料，并节省带传动所占的空间。链传动放到高速级（与电动机相连）的做法是错误的。由于链传动的多边形效应，即运动的不均匀性及动载荷，速度越高，冲击动载荷越大，链的寿命降低，因此链传动只能放在低速级，绝对不能与电动机相连。

【实例3】 图5-7中小带轮为主动轮，采用张紧轮将带张紧，在图a、b、c、d所示的四种张紧轮的布置方式中，哪个是合理的？为什么？（注：最小轮为张紧轮）

图5-7 实例3示意图

解：图d所示的方案合理。张紧轮应该装在松边（所需张紧力小）；在内侧张紧比在外侧压紧好（带的应力变化小），在内侧张紧时应靠近大轮（对小轮包角影响小）外侧，压紧时应靠近小轮（有利于增加小轮包角）。

【实例4】 一个带式输送机的驱动装置如图5-8所示。已知小带轮基准直径d₁＝140mm，大带轮基准直径d₂＝400mm；输送带速度v＝0.3m/s，为提高生产率，拟在输送机载荷不变（即拉力F不变）的条件下，将输送带速度v提高到0.42m/s。有人建议把大带轮基准直径减小到280mm来实现这一要求，其余不变，减速器强度足够，这个建议是否合理？

解：在输送机拉力不变的条件下，将d₂由400mm降至280mm，其余不变，单纯从速度来看可以提高（因d₂减小，带的传动比减小，速度可提高），但传递的功率相应增加，工作机功率P′₁＝Fv/1000＝（F×0.42）/1000，在没改变速度之前工作机的功率为P₁＝Fv/1000＝（F×0.3）/1000，功率增加到原来的P′₁/P₁＝1.4倍，电动机及各传动件传递的功率都相应提高到原来的1.4倍。

单纯从带传动来看，因小带轮速度n₁不变，小带轮基准直径d₁也不变，则带速不变，单根带能传递的功率P₀不变，但传递的功率增大到原来的1.4倍，由根数公式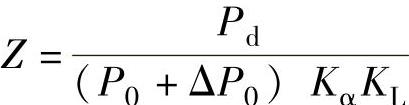来看，若忽略由于d₂变化而使K_α增大、ΔP₀减小等次要的影响，则P_d增大到原来的1.4倍，致使带的根数也应增加到原来的1.4倍（实际上不可能恰好是1.4倍），因此只有增加带的根数或选用截面更大的带型，才能满足要求；同时应对联轴器、轴承、键等零件重新校核，电动机功率是否满足也必须考虑。

另一种方法是大带轮基准直径保持不变，而将小带轮基准直径增大，改变后的小带轮基准直径是：d′₁＝（v′/v）d₁＝（0.42/0.3）×140mm＝196mm，此时带速增大为原来的1.4倍，单根带能传递的功率P₀也将增大，并满足传动功率增大1.4倍的要求。当然，只要带速不大于25m/s，就可保持原来带型号和根数而满足要求，但带的更换周期可能会缩短些；传动的功率增大后，仍然要重新校核轴承、联轴器、键等传动件，并且还要考虑电动机功率是否够用。

此类题目主要应从功率入手，单纯改变带轮的几何尺寸不可行。

【实例5】 图5-9所示为两级变速装置，如变速过程中轴2上的功率不变，则应按哪一种转速计算带根数？试用公式进行分析。

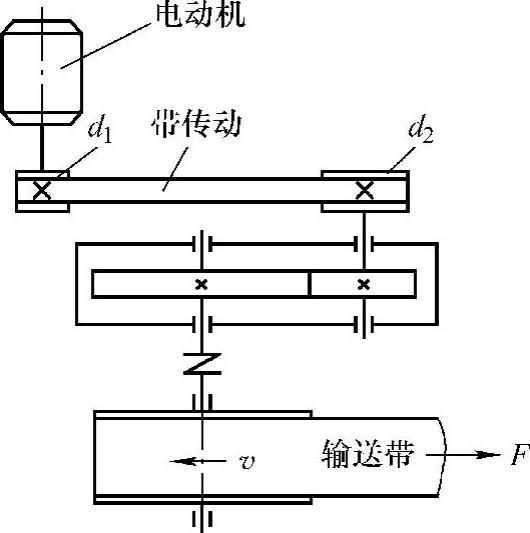
图5-8 实例4示意图

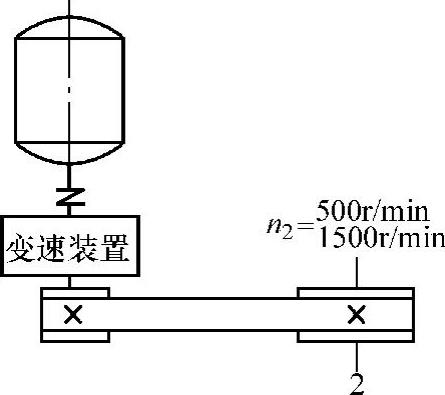
图5-9 实例5示意图

解：带的根数计算式为

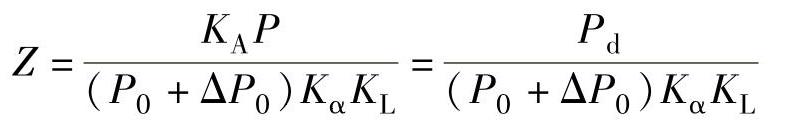
如果传动的功率P不变，原动机、工作机不变，则工作情况系数K_A不变，从而P_d不变。带轮、带长不变，则K_α、K_L也不变。而功率增量ΔP₀＝K_bn₁（1-1/K_i）（式中K_b为弯曲影响系数，与带的型号有关；K_i为传动比系数，与传动比有关），当型号不变时，K_b不变；传动比不变，则K_i不变。于是两种情况下ΔP₀仅与n₁有关，转速高时，ΔP₀大，两种转速相差1500/500＝3倍，因此ΔP₀相差3倍。

单根带传递功率为

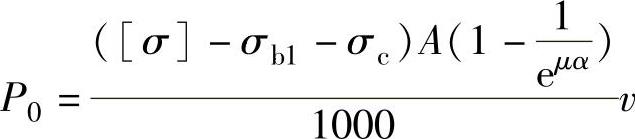
如果括号内的数为常数，则P₀与v成线性关系，但括号内的σ_c、［σ］皆与带速有关，因此P₀与v为非线性关系。v大，P₀也大，所需根数少，因此应按低速（n₂＝500r/min）设计带的根数，此时在高速时必然满足。

因P₀与v为非线性关系，因此在两种情况下计算出来的带根数并不相差3倍。

【实例6】 图5-10所示为一个带式制动器，已知制动轮的直径D＝100mm，制动轮的转矩T＝60N·m，制动杠杆的长l＝250mm，制动带和制动轮之间的摩擦因数_μ＝0.4。

1）求制动力Q；

2）分别计算当包角α＝210°、240°和270°时所要求的制动力Q；(www.xing528.com)

3）当制动轮的转矩T方向改变时，制动力Q又应为多大（取α＝180°）？

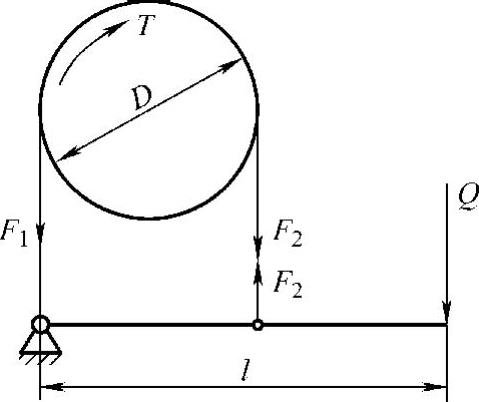
图5-10 实例6示意图（1）

4）试设计一种带式制动器，使得制动转矩T方向改变时，制动力Q大小保持不变。

解：必须了解带式制动器的工作原理：带式制动器和带传动的工作原理相同，但工作方式不同，前者用于制动，后者用于传动，再根据摩擦原理进行求解。

1.求制动力Q

制动轮的圆周力为

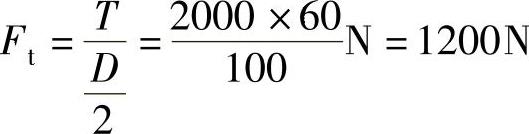
由力的平衡可知：

F_t＝F₁-F₂

又由欧拉公式知：

F₁/F₂＝e^μα

所以

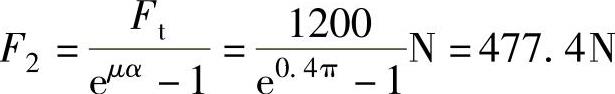
制动力为

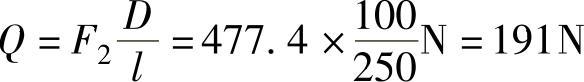
2.求当α＝210°、240°和270°时的制动力Q

当α＝210°时：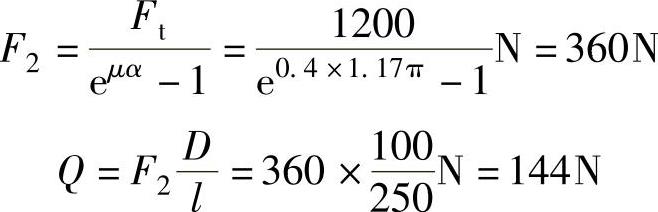

当α＝240°时：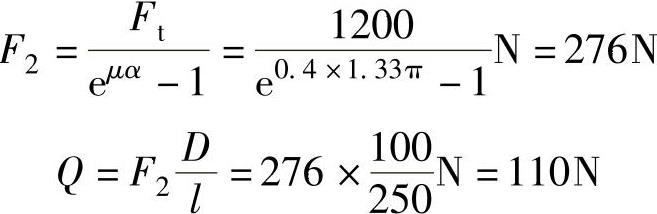

当α＝270°时：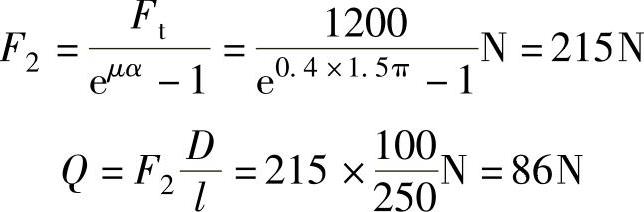

由以上结果可以看出，增大包角可增大带和带轮之间的摩擦力，因而可有效地减小制动力。

3.制动轮的转矩T改变方向时的制动力Q

由力的平衡关系可得

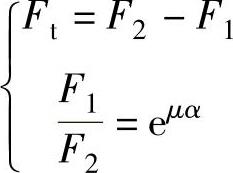
同样可以解出带端拉力F₂（紧边）：

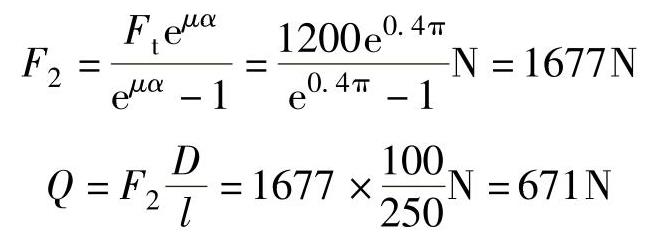
转矩T的方向改变之后，制动力要增大为原有制动力的e^μα倍，所以原设计不宜用于双向制动。

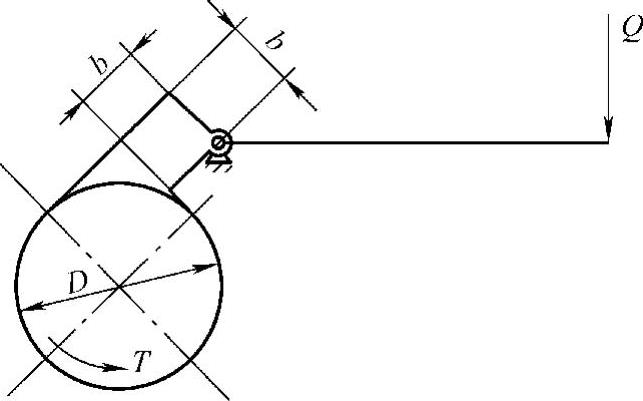
图5-11 实例6示意图（2）

4.设计双向带式制动装置

如图5-11所示，带的两端都固定在杠杆上，杠杆臂长b相等，在杠杆上加制动力Q，带的两端同时被拉紧。当制动轮转矩方向改变时，带端拉力F₁和F₂的大小虽然要相互交换，但两者对杠杆轴心的力矩和是保持不变的，因此制动力Q的大小与制动轮转矩方向的变化无关。